Learning to act by predicting the future Dosovitskiy & Koltun, ICLR’17
The Direct Future Prediction (DFP) model won the ‘Full Deathmatch’ track of the Visual Doom AI Competion in 2016. The competition pits agents against each other, with their performance measured by how many ‘frags’ they get. (A frag is a kill, apparently – not really my scene!). The action takes place in environments which the agents have never seen before. DFP outperformed the second best submission by more than 50% even though its model architecture is simpler and it received less supervisory training.
How does DFP perform so well? By re-thinking the fundamental approach to learning gameplay (or ‘sensorimotor control in immersive environments’ as it’s called in the paper!).
Machine learning problems are commonly divided into three classes: supervised, unsupervised, and reinforcement learning. In this view, supervised learning is concerned with learning input-output mappings, unsupervised learning aims to find hidden structure in data, and reinforcement learning deals with goal-directed behavior.
(Very nicely expressed!).
So goal-directed problems such as learning to perform well in a deathmatch seem to most naturally fit with reinforcement learning. And indeed we’ve seen DQN and A3C used for gameplay in earlier editions of The Morning Paper, as well as the deep reinforcement learning approach of “Playing FPS Games with Deep Reinforcement Learning“.
But there’s another view on the best way to tackle the problem, that goes way back:
The supervised learning (SL) perspective on learning to act by interacting with the environment dates back decades. Jordan & Rumelhart (1992) analyze this approach, review early work, and argue that the choice of SL versus RL should be guided by the characteristics of the environment. Their analysis suggests that RL may be more efficient when the environment provides only a sparse scalar reward signal, whereas SL can be advantageous when temporally dense multidimensional feedback is available.
For “temporally dense multidimensional feedback” think “short feedback loops with lots of information.”
Dosovitskiy & Koltun observe that the combination of a sensory stream (e.g., video frames from Doom) and a measurement stream (e.g., health, ammunition levels, number of adversaries in Doom) do indeed provide for the kind of rich supervisory signal that allow the problem to be reformulated as a supervised learning problem.
Our approach departs from the reward-based formalization commonly used in RL. Instead of a monolithic state and a scalar reward, we consider a stream of sensory input
and a stream of measurements
. The sensory stream is typically high-dimensional and may include the raw visual, auditory, and tactile input. The measurement stream has lower dimensionality and constitutes a set of data that pertain to the agent’s current state.
Instead of directly training an agent to maximise a reward, the agent is trained to predict the effect of different actions on future measurements, conditioned by the present sensory input, measurements, and goal.
Assuming that the goal can be expressed in terms of future measurements, predicting these provides all the information necessary to support action. This reduces sensorimotor control to supervised learning while supporting learning from raw experience and without extraneous data.
All the agent has to do is act, and observe the effects of its actions: the measurement stream provides ‘rich and temporally dense’ supervision that can stabilise and accelerate training.
High level overview
At every time step the agent receives an observation
with structure
where
is the raw sensory input and
is a set of measurements. The measurement vector differs from the other sensory inputs in two important ways: (i) it is what the agent will try to predict, and (ii) goals are expressed in terms of it. More specifically, goals are defined in terms of differences between current and future measurements over time. Any parametric function can be used, and the experiments in this paper use goals expressed as a simple linear combination of future measurements.
A parameterized function approximator, F is used to predict future measurements. The prediction is a function of the current observation, the considered action, and the goal. Once trained, a deployed agent can make predictions for all possible actions, and choose the action that yields the best predicted outcome in accordance with its current goal (which need not be identical to any goal seen during training).
The predictor F is trained on experiences collected by the agent itself, through interacting with the environment. The loss function is based on sum of the squared distances between the predicted measurement values and the actually observed values.
Two training regimes were evaluated: one in which the goal vector is fixed throughout the training process, and one in which the goal vector for each training episode is generated at random.
In both regimes, the agent follows an ε-greedy policy: it acts greedily according to the current goal with probability 1 – ε, and selects a random action with probability ε. The value of ε is initially set to 1 and is decreased during training according to a fixed schedule.
The predictor network
The predictor F is a deep network that looks like this:
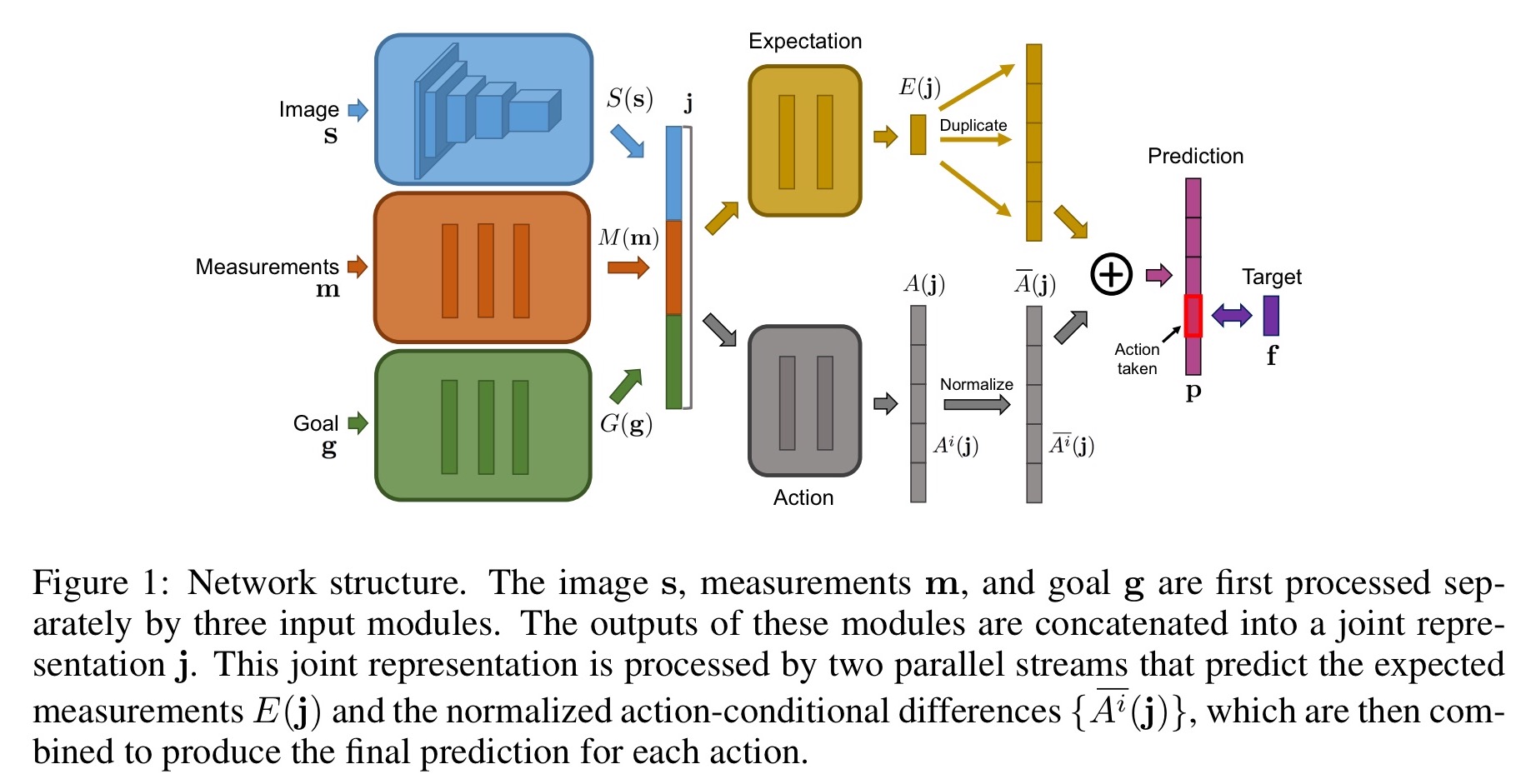
There are three input modules: a perception module S, which processes the sensory input (in the experiment, S is a convolutional network processing an input image); a measurement module M, and a goal module G. The outputs of all three are concatenated.
Future measurements are predicted based on this input representation. The network emits predictions of future measurements for all actions at once… we build on the ideas of Wang et al. (2016) and split the prediction module into two streams: an expectation stream and an action stream.
The expectation stream predicts the average of the future measurements across all potential actions. The action stream considers actions individually. A normalisation layer following the action stream subtracts the average future action value from all of the predicted action values. In this way, when the two are recombined the expectation stream is forced to compensate by predicting the average.
The final stage of the network sums the expectation stream and the action stream predictions, to give a prediction of future measurements for each action.
Let’s play Doom!
The ViZDoom platform is used for evaluation.
We compare the presented approach to state-of-the-art deep RL methods in four scenarios of increasing difficulty…
- Basic: gathering health kits in a square room
- Navigation: gathering health kits and avoiding poison vials in a maze
- Battle: defending against adversaries while gathering health and ammunition in a maze
- Battle 2: as above, but with a more complex maze.
The agent can move forward or backward, turn left or right, strafe left or right, run, and shoot. Any combination of these eight actions can be used, resulting in 256 possible actions. The agent is given three measurements: health, ammunition, and frag count.
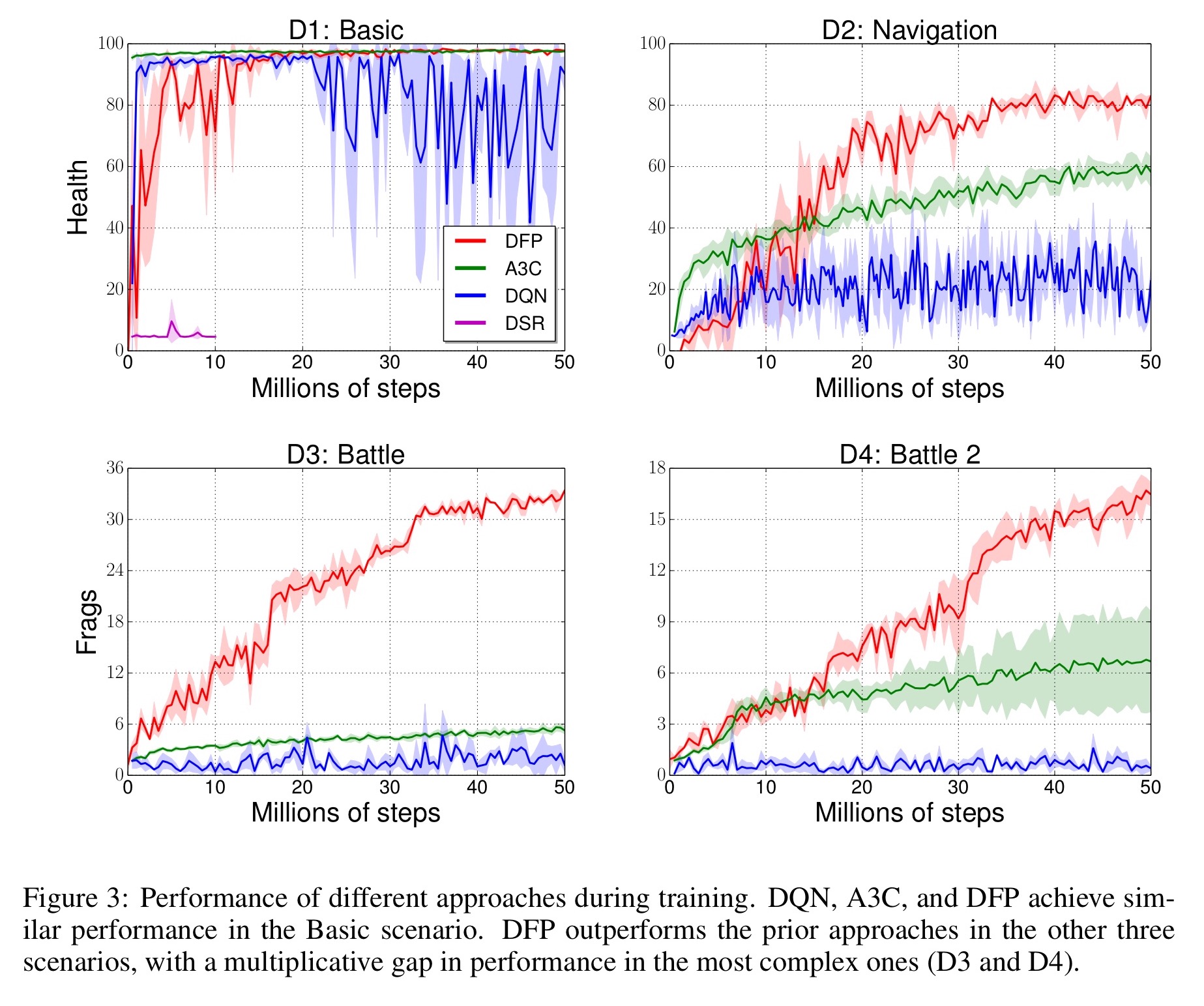
DFP (this paper) is compared against DQN (baseline for performance on Atari games), A3C (regarded as state-of-the-art in this area), and DSR (described in a recent technical report and also evaluated in ViZDoom). Here we can see a comparison of the performance levels reached during training:
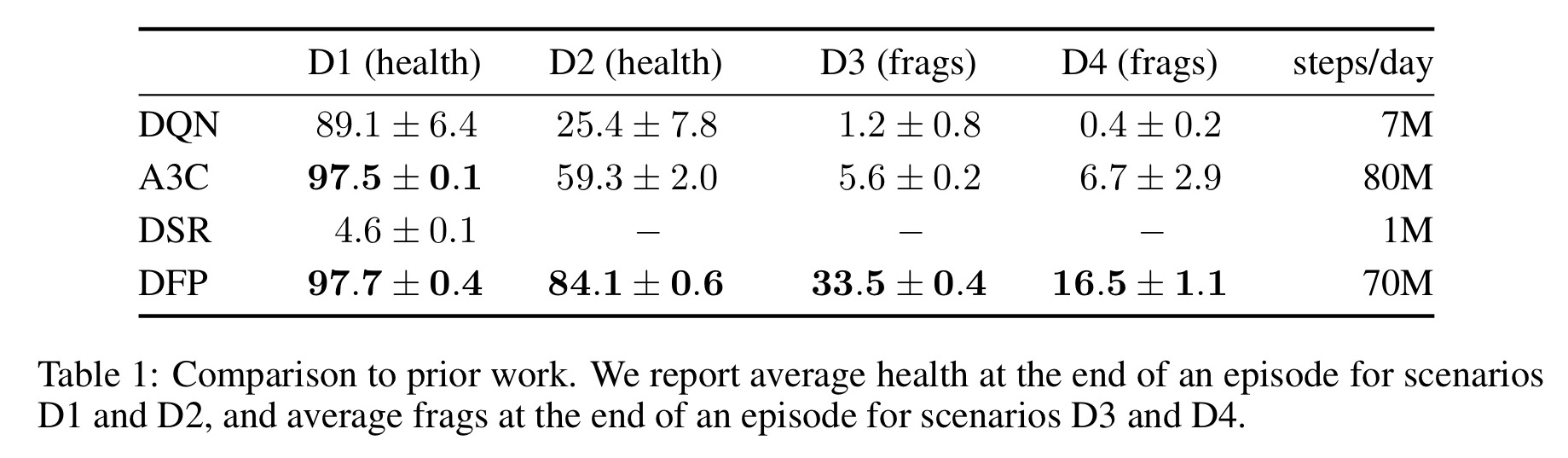
And here’s how well they do after training:
Far more interesting than staring at the table though, is to watch them play via this video:
[youtube https://www.youtube.com/watch?v=rPKwMWFo7Nk&w=854&h=480]
We now evaluate the ability of the presented approach to learn without a fixed goal at training time, and adapt to varying goals at test time. These experiments are performed in the Battle scenario. We use three training regimes: (a) fixed goal vector during training, (b) random goal vector with each value sampled uniformly from [0, 1] for every episode, and (c) random goal vector with each value sampled uniformly from [−1, 1] for every episode.
Here we see the results:
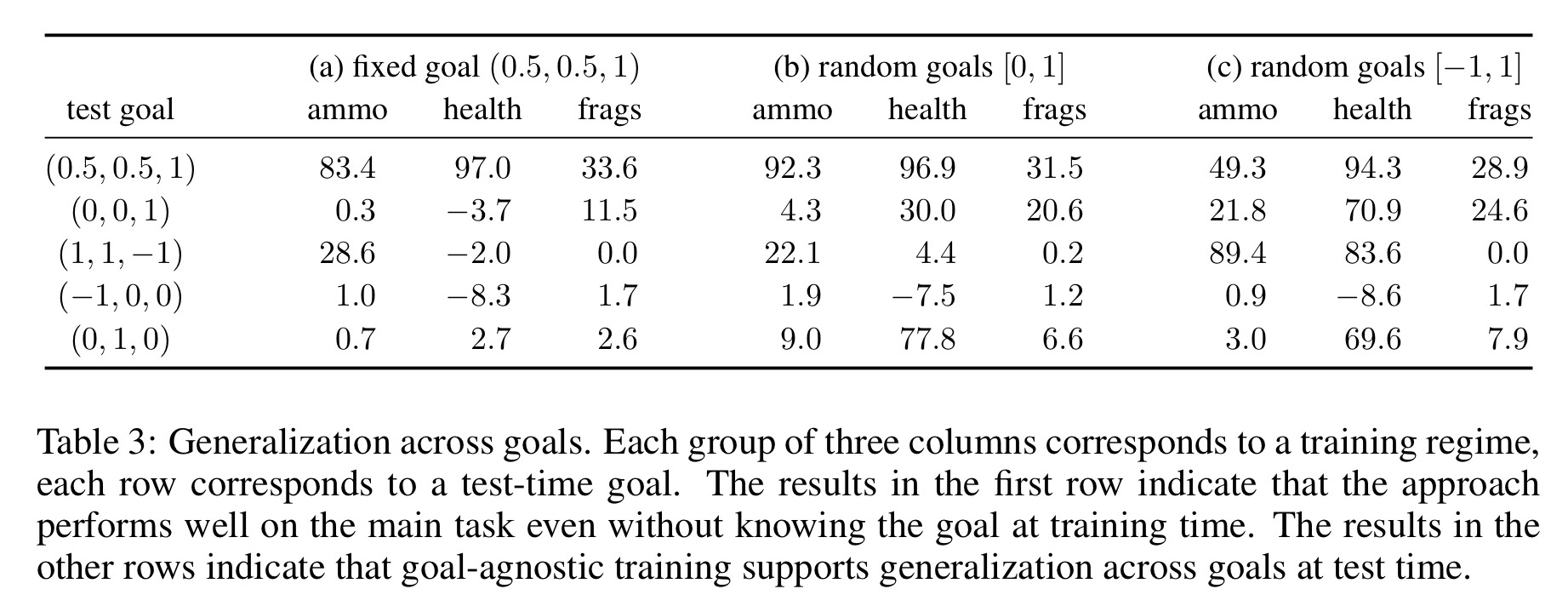
Models trained without knowing the goal in advance (b,c) perform nearly as well as a dedicated model trained for the eventual goal (a). All models generalise to new goals, but those trained with a variety of goals (b,c) generalise much better.
An ablation study showed that:
… predicting multiple measurements significantly improves the performance of the learned model, even when it is evaluated by only one of those measurements. Predicting measurements at multiple futures is also beneficial. This supports the intuition that a dense flow of multivariate measurements is a better training signal than a scalar reward.
Where next?
Our experiments have demonstrated that this simple approach outperforms sophisticated deep reinforcement learning formulations on challenging tasks in immersive environments… The presented work can be extended in multiple ways that are important for broadening the range of behaviors that can be learned.
- The present model is purely reactive, a memory component could be integrated and ‘may yield substantial advances.’
- Temporal abstraction and hierarchical organisation of learned skills will likely be necessary for significant progress in behavioural sophistication.
- The ideas could be applied to continuous actions (not just discrete action spaces as in this work)
- Predicting features learned directly from rich sensory input could blur the distinction between sensory and measurement streams.