Understanding deep learning requires re-thinking generalization Zhang et al., ICLR’17
This paper has a wonderful combination of properties: the results are easy to understand, somewhat surprising, and then leave you pondering over what it all might mean for a long while afterwards!
The question the authors set out to answer was this:
What is it that distinguishes neural networks that generalize well from those that don’t? A satisfying answer to this question would not only help to make neural networks more interpretable, but it might also lead to more principled and reliable model architecture design.
By “generalize well,” the authors simply mean “what causes a network that performs well on training data to also perform well on the (held out) test data?” (As opposed to transfer learning, which involves applying the trained network to a related but different problem). If you think about that for a moment, the question pretty much boils down to “why do neural networks work as well as they do?” Generalisation is the difference between just memorising portions of the training data and parroting it back, and actually developing some meaningful intuition about the dataset that can be used to make predictions. So it would be somewhat troubling, would it not, if the answer to the question “why do neural networks work (generalize) as well as they do?” turned out to be “we don’t really know!”
The curious case of the random labels
Our story begins in a familiar place – the CIFAR 10 (50,000 training images split across 10 classes, 10,000 validation images) and the ILSVRC (ImageNet) 2012 (1,281,167 training, 50,000 validation images, 1000 classes) datasets and variations of the Inception network architecture.
Train the networks using the training data, and you won’t be surprised to hear that they can reach zero errors on the training set. This is highly indicative of overfitting – memorising training examples rather than learning true predictive features. We can use techniques such as regularisation to combat overfitting, leading to networks that generalise better. More on that later.
Take the same training data, but this time randomly jumble the labels (i.e., such that there is no longer any genuine correspondence between the label and what’s in the image). Train the networks using these random labels and what do you get? Zero training error!
In [this] case, there is no longer any relationship between the instances and the class labels. As a result, learning is impossible. Intuition suggests that this impossibility should manifest itself clearly during training, e.g., by training not converging or slowing down substantially. To our suprise, several properties of the training process for multiple standard architectures is largely unaffected by this transformation of the labels.
As the authors succinctly put it, “Deep neural networks easily fit random labels.” Here are three key observations from this first experiment:
- The effective capacity of neural networks is sufficient for memorising the entire data set.
- Even optimisation on random labels remains easy. In fact, training time increases by only a small constant factor compared with training on the true labels.
- Randomising labels is solely a data transformation, leaving all other properties of the learning problem unchanged.
If you take the network trained on random labels, and then see how well it performs on the test data, it of course doesn’t do very well at all because it hasn’t truly learned anything about the dataset. A fancy way of saying this is that it has a high generalisation error. Put all this together and you realise that:
… by randomizing labels alone we can force the generalization error of a model to jump up considerably without changing the model, its size, hyperparameters, or the optimizer. We establish this fact for several different standard architectures trained on the CIFAR 10 and ImageNet classification benchmarks. (Emphasis mine).
Or in other words: the model, its size, hyperparameters, and the optimiser cannot explain the generalisation performance of state-of-the-art neural networks. This must be the case because the generalisation performance can vary significantly while they all remain unchanged.
The even more curious case of the random images
What happens if we don’t just mess with the labels, but we also mess with the images themselves. In fact, what if just replace the true images with random noise?? In the figures this is labeled as the ‘Gaussian’ experiment because a Gaussian distribution with matching mean and variance to the original image dataset is used to generate random pixels for each image.
In turns out that what happens is the networks train to zero training error still, but they get there even faster than the random labels case! A hypothesis for why this happens is that the random pixel images are more separated from each other than the random label case of images that originally all belonged to the same class, but now must be learned as differing classes due to label swaps.
The team experiment with a spectrum of changes introducing different degrees and kinds of randomisation into the dataset:
- true labels (original dataset without modification)
- partially corrupted labels (mess with some of the labels)
- random labels (mess with all of the labels)
- shuffled pixels (choose a pixel permutation, and then apply it uniformly to all images)
- random pixels (apply a different random permutation to each image independently)
- Guassian (just make stuff up for each image, as described previously)
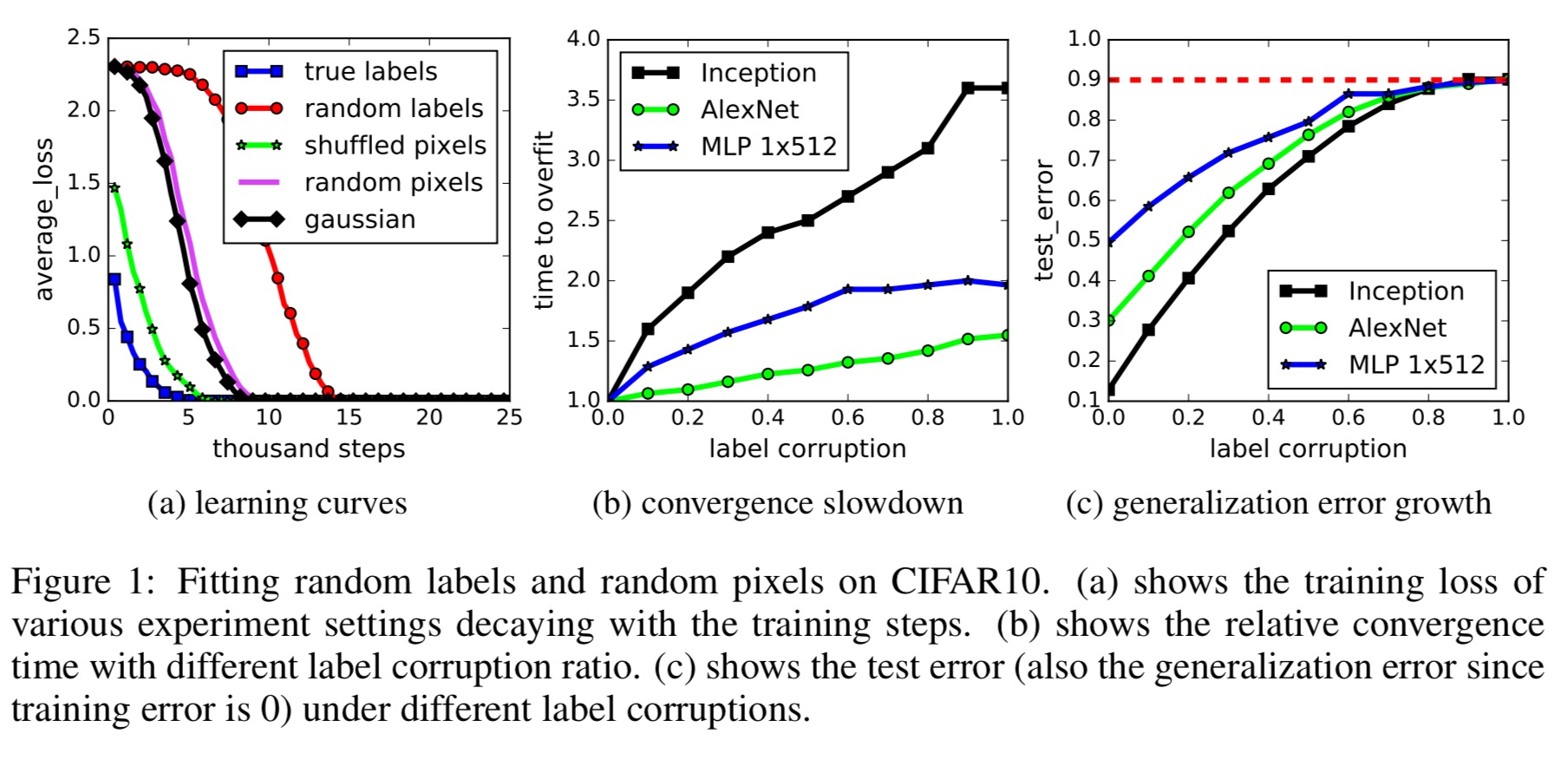
All the way along the spectrum, the networks are still able to perfectly fit the training data.
We furthermore vary the amount of randomization, interpolating smoothly between the case of no noise and complete noise. This leads to a range of intermediate learning problems where there remains some level of signal in the labels. We observe a steady deterioration of the generalization error as we increase the noise level. This shows that neural networks are able to capture the remaining signal in the data, while at the same time fit the noisy part using brute-force.
For me that last sentence is key. Certain choices we make in model architecture clearly do make a difference in the ability of a model to generalise (otherwise all architectures would generalise the same). The best generalising network in the world is still going to have to fallback on memorisation when there is no other true signal in the data though. So maybe we need a way to tease apart the true potential for generalisation that exists in the dataset, and how efficient a given model architecture is at capturing this latent potential. A simple way of doing that is to train different architectures on the same dataset! (Which we do all the time of course). That still doesn’t help us with the original quest though – understanding why some models generalise better than others.
Regularization to the rescue?
The model architecture itself is clearly not a sufficient regulariser (can’t prevent overfitting / memorising). But what about commonly used regularisation techniques?
We show that explicit forms of regularization, such as weight decay, dropout, and data augmentation, do not adequately explain the generalization error of neural networks: Explicit regularization may improve generalization performance, but is neither necessary nor by itself sufficient for controlling generalization error.
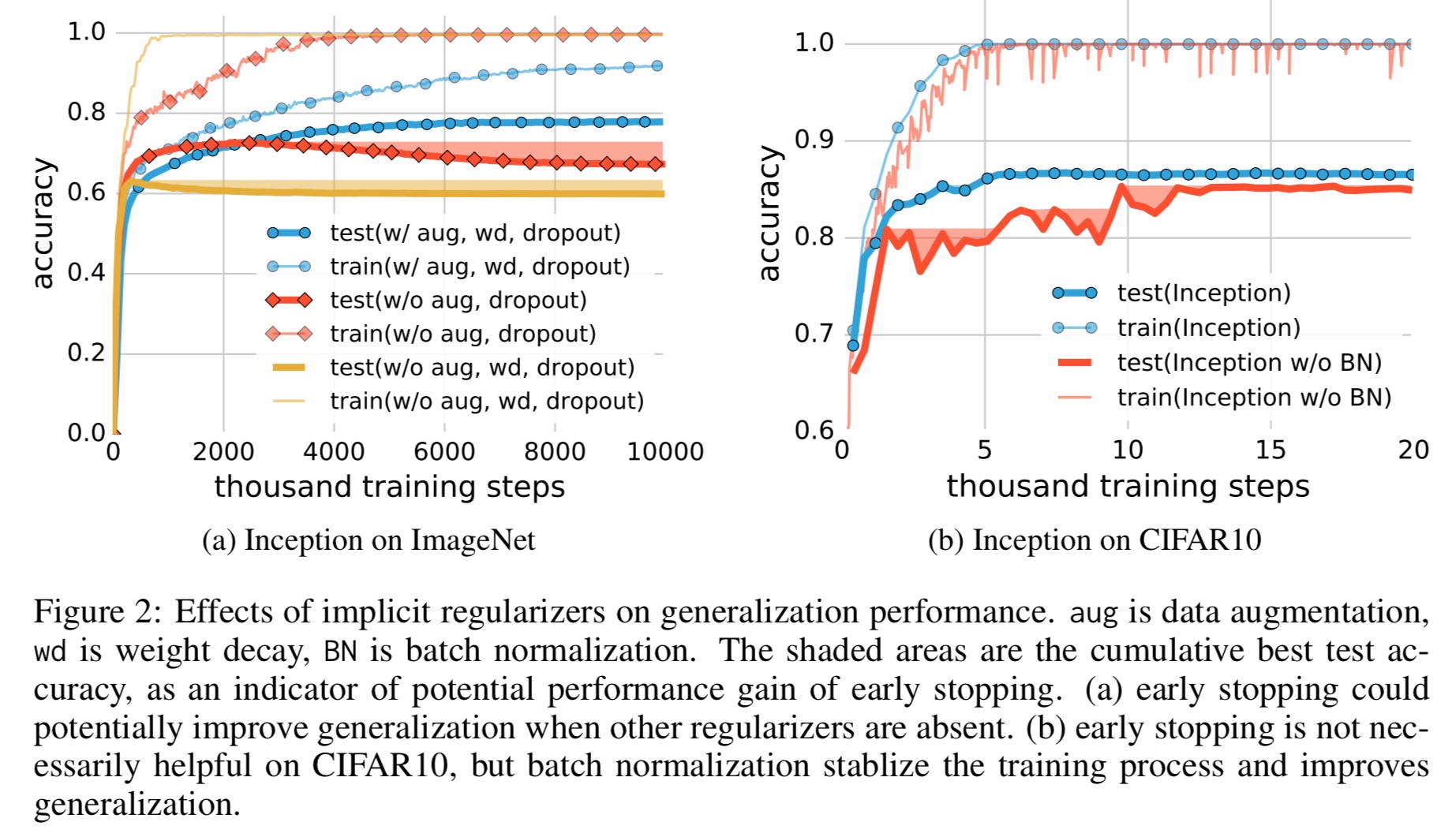
Explicit regularisation seems to be more of a tuning parameter that helps improve generalisation, but its absence does not necessarily imply poor generalisation error. It is certainly not the case that not all models that fit the training data generalise well though. An interesting piece of analysis in the paper shows that we pick up a certain amount of regularisation just through the process of using gradient descent:
We analyze how SGD acts as an implicit regularizer. For linear models, SGD always converges to a solution with small norm. Hence, the algorithm itself is implicitly regularizing the solution… Though this doesn’t explain why certain architectures generalize better than other architectures, it does suggest that more investigation is needed to understand exactly what the properties are that are inherited by models trained using SGD.
The effective capacity of machine learning models
Consider the case of neural networks working with a finite sample size of n. If a network has p parameters, where p is greater than n, then even a simple two-layer neural network can represent any function of the input sample. The authors prove (in an appendix), the following theorem:
There exists a two-layer neural network with ReLU activations and 2n + d weights that can represent any function on a sample of size n in d dimensions.
Even depth-2 networks of linear size can already represent any labeling of the training data!
So where does this all leave us?
This situation poses a conceptual challenge to statistical learning theory as traditional measures of model complexity struggle to explain the generalization ability of large artificial neural networks. We argue that we have yet to discover a precise formal measure under which these enormous models are simple. Another insight resulting from our experiments is that optimization continues to be empirically easy even if the resulting model does not generalize. This shows that the reasons for why optimization is empirically easy must be different from the true cause of generalization.