PowerGraph: Distributed Graph-Parallel Computation on Natural Graphs – Gonzalez et al. 2012
A lot of the time, we want to perform computations on graphs that model the real world. As we saw in Exploring Complex Networks, such graphs often follow a power-law degree distribution (i.e., a few nodes are very highly connected, and many nodes are very weakly connected). The probability that a given node has degree (no. of connected edges) d, is proportional to d-α.
Graph-parallel abstractions rely on each vertex having a small neighborhood to maximize parallelism and effective partitioning to minimize communication. However, graphs derived from real-world phenomena, like social networks and the web, typically have power-law degree distributions, which implies that a small subset of the vertices connects to a large fraction of the graph. Furthermore, power-law graphs are difficult to partition and represent in a distributed environment.
Boom! (I’m told that’s what the hipsters say these days 😉 ).
PowerGraph introduces a better way of partitioning power-law graphs, a programming abstraction that supports parallel execution within a vertex computation, and a runtime engine that efficiently supports this model.
Partitioning Power-Law Graphs
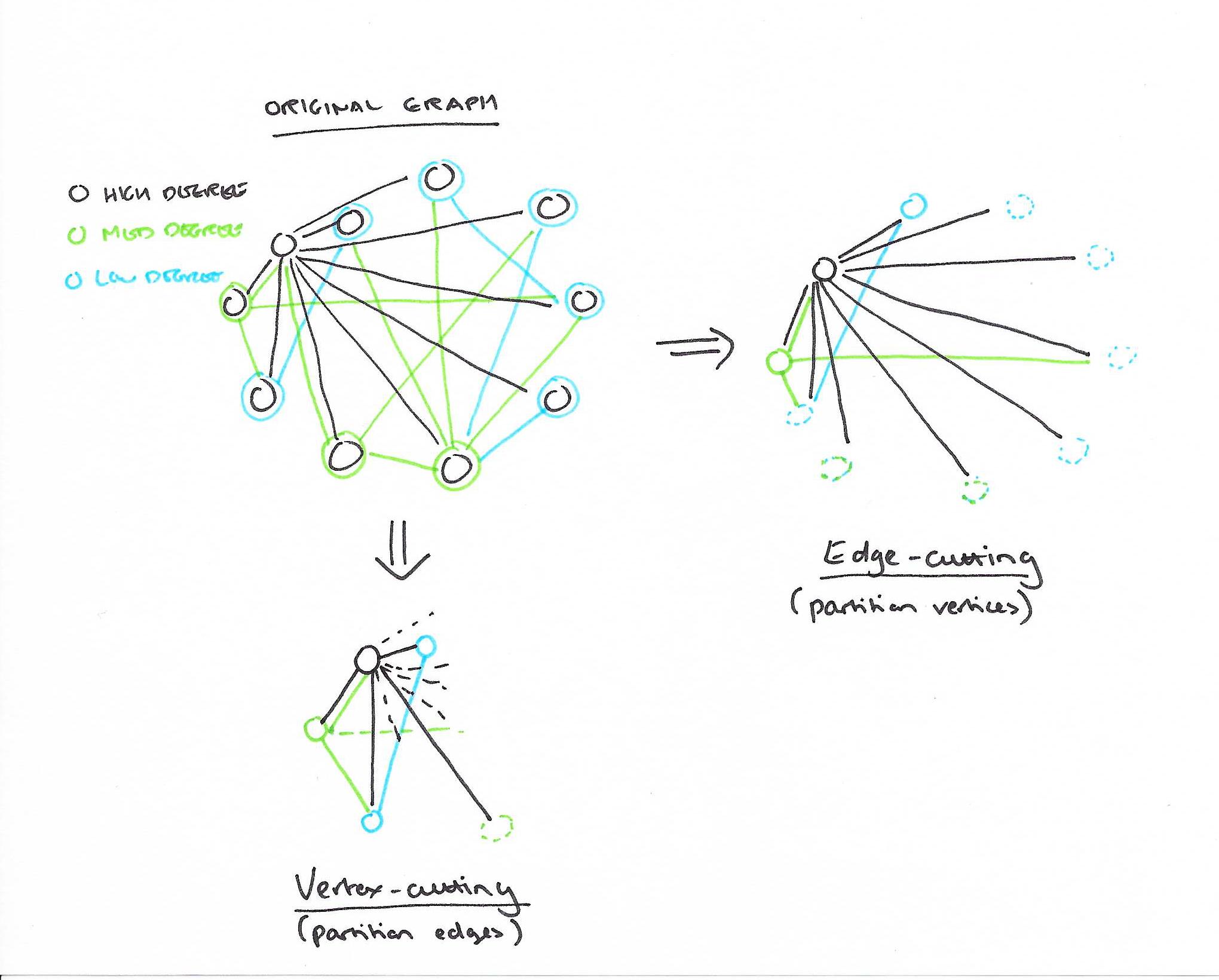
The fundamental insight in this paper is that with a power-law based graph, if you partition the graph based on vertices (known as edge-cutting, since you snip the edges that connect vertices to form the partitioning), then a very high degree vertex and all of its edges fall solely within one partition.
The skewed degree distribution implies that a small fraction of the vertices are adjacent to a large fraction of the edges. For example, one percent of the vertices in the Twitter web-graph are adjacent to nearly half of the edges. This concentration of edges results in a star-like motif which presents challenges for existing graph-parallel abstractions:
- substantial work-imbalance since the storage, communication, and computation complexity are linear in the degree
- difficulty in partitioning – which e.g. both GraphLab and Pregel depend on in order to perform well.
- single-node storage challenges: graph parallel abstractions must locally store the adjacency information for each vertex, hence high-degree vertices can exceed the memory capacity of a single machine
- hard to parallelize effectively since existing graph-parallel abstractions do not parallelize within individual vertex programs.
In fact, if you construct an n-way edge-cut to partition a graph across n machines, the probability that the vertices on either end of an edge are assigned to different machines is 1 – 1/n. Even with only 10 machines, this means that on average 9/10 edges are cut.
PowerGraph introduces an abstraction that allows a single vertex program to span multiple machines (unlike GraphLab and Pregel) – more on this soon. Therefore we can partition edges across nodes with a vertex-cut.
…we can improve work balance and reduce communication and storage overhead by evenly assigning edges to machines and allowing vertices to span machines. Each machine only stores the edge information for the edges assigned to that machine, evenly distributing the massive amounts of edge data. Since each edge is stored exactly once, changes to edge data do not need to be communicated. However, changes to vertex must be copied to all the machines it spans, thus the storage and network overhead depend on the number of machines spanned by each vertex.
For each vertex that is cut (has multiple replicas), one of the replicas is randomly assigned the master role, the rest are read-only replicas.
Here’s a quick sketch I did of a small power-law graph showing the difference between an edge-cut and a vertex-cut.
Vertex-cuts address the major issues associated with edge-cuts in power-law graphs. Percolation theory suggests that power-law graphs have good vertex-cuts. Intuitively, by cutting a small fraction of the very high degree vertices we can quickly shatter a graph. Furthermore, because the balance constraint (Eq. 5.4) ensures that edges are uniformly distributed over machines, we naturally achieve improved work balance even in the presence of very high-degree vertices.
A simple way to vertex cut is simply to randomly assign edges to machines. It turns out that a random (hash) edge placement achieves near-perfect balance on large graphs. We can do even better than random with a greedy heuristic that places the next edge on the machine that minimizes the conditional expected replication (of vertices) factor. This can be done via a centralized coordinated node, or the greedy heuristic can be run independently on each machine (oblivious). The oblivious strategy balances a relatively low replication factor while only slightly increasing run (load) time. For the Twitter graph, greedy heuristics give an order-of-magnitude reduction in the replication factor.
the vertex cut model is also highly effective for regular graphs since in the event that a good edge-cut can be found it can be converted to a better vertex cut.
The Gather, Apply, Scatter abstraction
Vertex-cutting depends on a graph abstraction that supports parallelization within a vertex computation. Gonzalez et al. introduce the very elegant Gather, Apply, and Scatter (GAS) model for this purpose.
While the implementation of MLDM vertex-programs in GraphLab and Pregel differ in how they collect and disseminate information, they share a common overall structure. To characterize this common structure and differentiate between vertex and edge specific computation we introduce the GAS model of graph computation.
The GAS model has three conceptual phases: gather, apply, and scatter. Consider some vertex u. In the gather phase information about adjacent vertices and edges is collected through a generalized sum function defined by the user. This function must be commutative and associative and could be e.g. a numerical sum, or a union.
In the apply phase a user-defined apply function updates the value of the central vertex u : it is passed the data of the vertex itself, and the sum calculated in the gather phase.
In the scatter phase the new value of the u is used to update the data on adjacent edges. For each edge (u,v), the scatter function is passed the new value of u, and the current values of the edge (u,v) and the vertex v. The result of the function becomes the new value of edge (u,v).
…PowerGraph (is) a new graph-parallel abstraction that eliminates the degree dependence of the vertex-program by directly exploiting the GAS decomposition to factor vertex-programs over edges. By lifting the Gather and Scatter phases into the abstraction, PowerGraph is able to retain the natural “think-like-a-vertex” philosophy while distributing the computation of a single vertex-program over the entire cluster.
A GAS vertex program is an implementation of an interface that supplies user-defined gather, sum, apply, and scatter functions. Each function is invoked in stages by the PowerGraph Engine.
Gather and sum act like a map and reduce in collecting information from the neighbourhood. gather is invoked in parallel on the edges adjacent to u, and the user can specify whether to include all edges, in edges, out edges or none of the edges.
The size of the accumulator (produced by sum) and complexity of the apply function play a central role in determining the network and storage efficiency of the PowerGraph abstraction and should be sub-linear and ideally constant in the degree.
In the scatter phase the scatter function is invoked in parallel on the edges adjacent to_u_, and again the user can specify which set of edges should be included.
As an example, …
In graph coloring the gather and sum functions collect the set of colors on adjacent vertices, the apply function computes a new color, and the scatter function activates adjacent vertices if they violate the coloring constraint.
PowerGraph Engine
In many cases a vertex-program will be triggered in response to a change in a few of its neighbors. The gather operation is then repeatedly invoked on all neighbors, many of which remain unchanged, thereby wasting computation cycles. For many algorithms it is possible to dynamically maintain the result of the gather phase and skip the gather on subsequent iterations.
The engine supports this by maintaining a cache of the accumulator value from the previous gather phase for each vertex. The scatter function can optionally return a delta which is added to the cached accumulator using the user-provided sum function. If no delta is returned, the cache is cleared.
The PowerGraph engine itself is in charge of scheduling the vertex-program on active vertices. It supports both synchronous and asynchronous scheduling, which to “different tradeoffs in algorithm performance, system performance, and determinism.” The synchronous version uses a Bulk Synchronous Parallel model where a super-step corresponds to synchronously running a gather-apply-scatter minor-step on all active vertices. The asynchronous model supports GraphLab’s serializability guarantees.
Ensuring serializability for graph-parallel computation is equivalent to solving the dining philosophers problem where each vertex is a philosopher, and each edge is a fork. GraphLab implements Dijkstra’s solution where forks are acquired sequentially according to a total ordering. Instead, we implement the Chandy-Misra solution which acquires all forks simultaneously, permitting a high degree of parallelism.
See The Drinking Philosopher’s Problem.
Fault-tolerance is achieved through snapshotting.