Blogel: A Block-Centric Framework for Distributed Computation on Real-World Graphs – Yan et al. 2014

We’ve looked at a lot of different Graph-processing systems over the last couple of weeks (onto a new topic next week I promise!), and despite a variety of different implementation and execution models, one thing they all have in common is a vertex-centric programming model. The abstractions you make available to a programmer determine the algorithms that can be expressed, and the efficiency of those expressions. The big idea in today’s paper choice, Blogel, is the introduction of a two-level abstraction: you can still compute at the vertex level, but you can also compute at the block level (collection of connected vertices).

The motivation for introducing block-based compute is the common characteristics of many real-world networks:

• A skewed degree distribution following a power law (as we’ve seen before with PowerGraph),
• Large diameter graphs (which cause many algorithms to require a large number of iterations), and
• Relatively high density graphs (high average degree of vertices)

We’ve seen the introduction of vertex-cuttting to cope with skewed degree distributions before, but nothing that speaks to the diameter and density characteristics.

Large diameter graphs can lead to an excessive number of iterations (supersteps) in vertex-centric models:

For processing graphs with a large diameter δ, the message (or neighbor) propagation paradigm of the vertex-centric model often leads to algorithms that require O(δ) rounds (also called supersteps) of computation. For example, a single-source shortest path algorithm in [11] takes 10,789 supersteps on a USA road network. Apart from spatial networks, some large web graphs also have large diameters (from a few hundred to thousands). For example, the vertex-centric system in [14] takes 2,450 rounds for computing strongly connected components on a web graph.

High density graphs can lead to excessive messaging:

…for many real-world graphs including power-law graphs such as social networks and mobile phone networks, the average vertex degree is large. Also, most large real-world graphs have a high-density core (e.g., the k-core and k-truss of these graphs). Higher density implies heavier message passing for vertex-centric systems.

Blogel is conceptually similar to Pregel, but can work in coarser-grained units called blocks. A block is a connected sub-graph, and message exchanges occur between blocks. The number of blocks is usually orders of magnitude less than the number of vertices, which can significantly reduce the overall workload (we’ll see some examples later). The block-based model relies on an effective partitioning of the graph into blocks in the first place, and a new graph Voronoi diagram based partitioner is introduced for this purpose.

Our experiments on large real-world graphs with up to hundreds of millions of vertices and billions of edges, and with different characteristics, verify that our block-centric system is orders of magnitude faster than the state-of-the-art vertex-centric systems. We also demonstrate that Blogel can effectively address the performance bottlenecks caused by the three adverse characteristics of real-world graphs.

(Blogel is compared against Giraph 1.0.0, Giraph++, and GraphLab 2.2, which incorporates the features of PowerGraph. More on what this means for the ‘order of magnitude’ claim tomorrow…).

Blogel’s Programming Model

A partitioner is used to partition a graph into blocks, where each block is a connected sub-graph of the original graph. Computation can be done at the vertex level, via a user-provided vertex-compute function (as in Pregel), and it can also be done at the block level, via a user-provided block-compute function. Blocks are assigned to workers.

A block has access to all its vertices, and can send messages to any block B or vertex v as long as worker(B) or worker(v) is available. Each B-worker maintains two message buffers, one for exchanging vertex-level messages and the other for exchanging block-level messages. A block also has a state indicating whether it is active, and may vote to halt.

Blogel can operate in block mode (B-mode), vertex mode (V-mode), or a combined vertex-and-block mode (VB-mode):

• In B-Mode Blogel only calls B-compute() for all its blocks, and only block-level message exchanges are allowed. A job terminates when all blocks voted to halt and there is no pending message for the next superstep.
• In V-Mode Blogel only calls V-compute() for all its vertices, and only vertex-level message exchanges are allowed. A job terminates when all vertices voted to halt and there is no pending message for the next superstep.
• In VB-Mode, in each superstep, a B-worker first calls V-compute() for all its vertices, and then calls B- compute() for all its blocks. If a vertex v receives a message at the beginning of a superstep, v is activated along with its block B = block(v), and B will call its B-compute() function. A job terminates only if all vertices and blocks voted to halt and there is no pending message for the next superstep.

Blogel also supports combiners and aggregators at both the block and vertex level.

The benefits of this model are most easily understood through a series of examples…

Example algorithms exploiting block computing

Connected Components

The Hash-Min algorithm for finding connected components computes the id of each connected component as the minimum vertex id of all the vertices within that component. In a vertex-centric model the algorithm proceeds as follows:

For the vertex-centric model, in superstep 1, each vertex v sets min(v) to be the smallest ID among id(v) and id(u) of all u ∈ neighborhood(v), broadcasts min(v) to all its neighbors, and votes to halt. In each later superstep, each vertex v receives messages from its neighbors; let min∗ be the smallest ID received, if min∗ < min(v), v sets min(v) = min∗ and broadcasts min∗ to its neighbors. All vertices vote to halt at the end of a superstep. When the process converges, min(v) = cc(v) for all v.

The vertex-centric model sends O(d_max) messages each round, where d_max is the maximum vertex degree in the graph.

With its block model, Blogel creates a block-level graph where each node is a block, and an edge between blocks represents any connection between a vertex in the source block and a vertex in the destination block. Blogel gets a big head-start for this algorithm too because each block is already known to be a connected sub-graph (so all vertices within it must ultimately share the same connected component id).

We then simply run Hash-Min on [the block graph] where blocks broadcast the smallest block ID that they have seen. Similar to the vertex-centric algorithm, each block B maintains a field min(B), and when the algorithm converges, all vertices v with the same min(block(v)) belong to one CC.

A real-world graph with skewed distributed is highly likely to have a giant connected component. Let the number of vertices in that component be n. If b is the average number of vertices in a block, then the algorithm requires at most O(n/b) messages each round.

For power-law graphs, d_max can approach n and n/b can be a few orders of magnitude smaller than d_max for a reasonable setting of b (e.g., b = 1000).

For the Friendster social network graph, the block-level algorithm used 372x fewer messages than the vertex-centric one, resulting in a 48x faster runtime.

Single-Source Shortest Path

SSSP computes a shortest path from s to every other vertex v ∈ V. In the vertex-centric algorithm, each vertex v maintains two pieces of state: the node preceding v on the shortest known path from s to v, and the length (dist(v)) of that path. Start at vertex v with dist(s) = 0, and distance for every other vertex set to infinity. In the first superstep s sends the message (s, dist(s), length(s,u)) to all of its neighbours u and votes to halt. In subsequent supersteps a vertex finds the neighbour with the shortest distance out of its received messages, and if this is less than its currently recorded distance it saves that neighbour as the preceding vertex and propogates new distance messages on its out edges. Then it votes to halt. The algorithm therefore terminates when no more outgoing messages are sent in a superstep.

The block-centric algorithm is more complicated… in each superstep V-compute() is first run for each vertex, but a vertex receiving a new shortest distance does not vote to halt and instead stays active.

Then, B-compute() is executed where each block B collects all its active vertices v into a priority queue Q (with dist(v) as the key), and makes these vertices vote to halt. B-compute() then runs Dijkstra’s algorithm on B using Q, which removes the vertex v ∈ Q with the smallest value of dist(v) from Q for processing each time. The out-neighbors u ∈ (v) are updated as follows. For each u ∈ V (B), if dist(v)+ l(v, u) < dist(u), we update (prev(u), dist(u)) to be (v, dist(v)+l(v, u)), and insert u into Q with key dist(u) if u is not a member of Q, or update dist(u) if u is already in Q. For each u not in V (B), a message (v, dist(v)+l(v, u)) is sent to u. B votes to halt when Q becomes empty. In the next superstep, if a vertex u receives a message, u is activated along with its block, and the block-centric computation repeats.

Running Dijkstra’s algorithm within the block saves a significant amount of communication cost since there is no message passing amongst vertices in the block. The algorithm also requires many less supersteps than the vertex-centric version. For large diameter graphs, it is one to two orders of magnitude faster.

PageRank and Reachability

Refer to the full paper for additional descriptions of PageRank and Reachability algorithms reworked to include block-level computing.

Voronoi Diagram based partitioning

“Efficient computation of blocks that give balanced workload is crucial to the performance of Blogel.” You can provide your own partitioner, but Blogel also provides an out-of-the-box Voronoi partitioner, and a 2D partitioner for graphs where vertices have (x,y) coordinates.

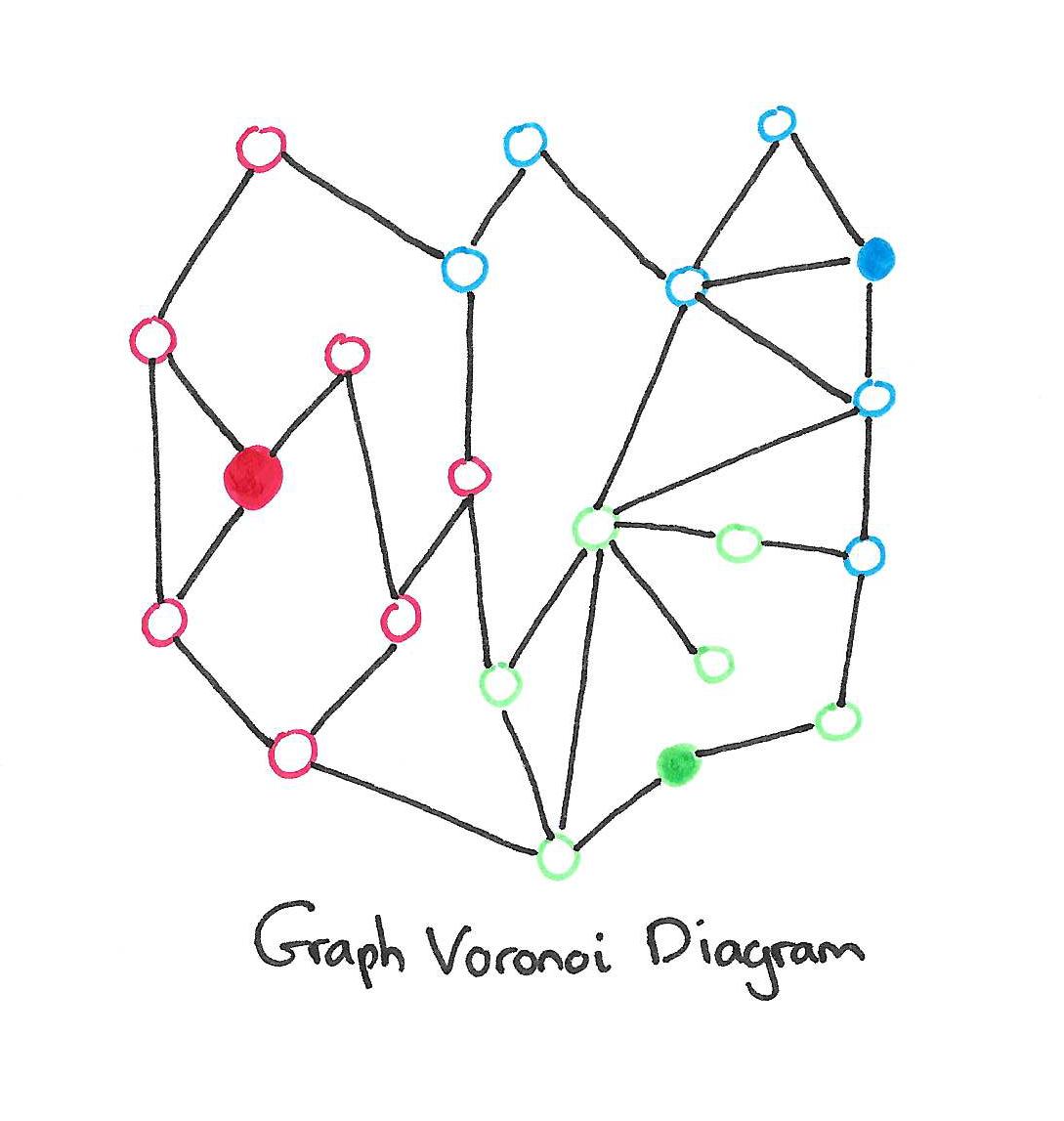
We first review the Graph Voronoi Diagram (GVD) of an undirected unweighted graph G = (V,E). Given a set of source vertices s1, s2, . . . , sk ∈ V , we define a partition of V : {V C(s1), V C(s2) , . . . , V C(sk)}, where a vertex v is in V C(si) only if si is closer to v (in terms of the number of hops) than any other source. Ties are broken arbitrarily. The set V C(si) is called the Voronoi cell of si, and the Voronoi cells of all sources form the GVD of G.

To put it more simply: pick a few seed vertices to form your clusters around. Add vertices to the cluster of the seed they are closest to in terms of hops. Break ties arbitrarily.

The basic approach to partitioning this way is as follows:

Our GVD partitioner works as follows, where we use a parameter b_maxto limit the maximum block size. Initially, each vertex v samples itself as a source with probability p_samp. Then, multi-source BFS is performed to partition the vertices into blocks. If the size of a block is larger than b_max, we set block(v) unassigned for any vertex v in the block (and reactivate v). We then perform another round of source sampling and multi-source BFS on those vertices v with block(v) unassigned, using a higher sampling probability. Here, we increase p_samp b y a factor of f (f ≥ 1) after each round in order to decrease the chance of obtaining an over-sized block. This process is repeated until the stop condition is met.

It is also possible to bound the number of supersteps for the above, in the case of large diameter graphs. When this process stops, there may still be some unassigned vertices. Sampling works well for large connected components, but less well when there are lots of very small ones.

Our solution to assigning blocks for small CCs is by the Hash-Min algorithm, which marks each small CC as a block using only a small number of supersteps.

Blogel’s GVD partitioner is much faster than the popular METIS partitioning algorithm under the author’s evaluations.