The Drinking Philosophers Problem – Chandy & Misra 1984

How could I resist a paper with a title like that! The Drinking Philosophers is referenced in the PowerGraph paper as a solution to the problem of serializable execution in graph-parallel computation. Vertices are philosophers, and edges are forks (drinks). Let’s take a look at how it works.

We propose a paradigm, the drinking philosophers problem,which captures the essence of conflict resolution problems in distributed systems.

Conflict resolution refers to situations where two or more processes attempt to carry out mutually exclusive actions simultaneously….

The resolution of such a conflict requires that some processes be treated differently from others in the sense that the conflict be resolved in favor of some processes and against other conflicting processes. If all processes in a set of conflicting processes are indistinguishable (i.e., if every property that holds for one process also holds for the others), then it is impossible to resolve conflicts between them without resorting to random selection. This is because any deterministic algorithm that selects one of the processes for favorable treatment must carry out the selection on the basis of some property that holds for that process and not for the others.

(Randomness can actually be very useful – for example, it allows you to beat the FLP impossibility result – but here randomness is ruled out).

…if we do not wish to use probabilistic algorithms to resolve conflicts, we must ensure the following invariant: Distinguishability. Distinguishability. In every state of the system at least one process in every set of conflicting processes must be distinguishable from the other processes of the set.

We probably also care about fairness – conflicts should not always be resolved to the detriment of a particular process for example. But…

If conflicts always occur in the same system state, a deterministic conflict resolution scheme will always resolve conflicts in the same way because the outcome of a deterministic scheme is a function of the system state. In this case conflict resolution will be unfair.

So somehow we need to manufacture things such that the states we obtain when conflict occurs are not always identical. Let’s start by looking at a model that requires some global knowledge, and then derive a variant that can act in a distributed manner with local action and knowledge only.

Consider a graph H in which each vertex represents a process, and there is an edge between two vertices if and only if there may be a conflict between them. The edge is directed, away from the process with higher precedence, and towards the process with lower precedence.

If H is acyclic, then the depth of a process in H is a distinguishing property by which a process can be distinguished from all processes that it may conflict with; depth of a process p in H is the maximum number of edges on any (directed) path to p from a process without any predecessors. Note that a process with no predecessor has depth 0. It follows that neighbors cannot have the same depth.

If H has a cycle of course this won’t work, so we’ll need a mechanism to ensure the graph is acyclic. To ensure fairness, we’ll also need to ensure that every process ‘rises to the top’ (i.e. to zero depth) in H in finite time. Thus we need to mutate H. We can’t change the vertices, so the only thing we can change is the direction of the edges. We can preserve the acyclic nature of the graph, and achieve fairness, with two simple rules:

1. The Acyclicity Rule: All edges incident on a process p may be simultaneously (i.e. in one atomic action) redirected toward p. This can’t form a cycle because there is no edge directed away from p after the transformation.
2. The Fairness Rule: Within finite time after a conflict is resolved in favour of a process p at depth 0, p must yield precedence to its neighbours.

The distributed implementation includes a scheme by which processes can make local decisions based on partial information of H. It’s time for the drinking philosophers…

Processes, called philosophers, are placed at the vertices of a finite undirected graph G with one philosopher at each vertex. A philosopher is in one of 3 states: (1) tranquil, (2) thirsty, or (3) drinking. Associated with each edge in G is a bottle. A philosopher can drink only from bottles associated with his incident edges. A tranquil philosopher may become thirsty. A thirsty philosopher needs a non-empty set of bottles that he wishes to drink from. He may need different sets of bottles for different drinking sessions. On holding all needed bottles, a thirsty philosopher starts drinking; a thirsty philosopher remains thirsty until he gets all bottles he needs to drink. On entering the drinking state a philosopher remains in that state for a finite period, after which he becomes tranquil. A philosopher may be in the tranquil state for an arbitrary period of time. Two philosophers are neighbors if and only if there is an edge between them in G. Neighbors may send messages to one another. Messages are delivered in arbitrary but finite time. Resources, such as bottles, are also encoded and transmitted as messages…

The solution must be fair, symmetric (all philosophers follow the same rules with no external priority etc.), economic in terms of number of messages, allow concurrent drinking, and be bounded in terms of number and size of messages in transit.

The drinkers problem is a general paradigm for modeling conflicts between processes. Neighboring philosophers will be prevented from drinking simultaneously if they wish to drink from the same bottle – this situation models conflicts for exclusive access to a common file. Neighboring philosophers may drink simultaneously from different bottles – this situation models processes writing into different files.

We know that we must prevent the system from entering into a state in which every philosopher is indistinguishable (for example, all drinking from their ‘left’ bottle), yet neither can we preclude valid states such as this. “We appear to be in a quandary because the constraints of symmetric processes, non-probabilistic solutions, and concurrency are incompatible for this problem. ” The quandary is resolved by using special ‘auxiliary’ resources. The dining philosophers problem is used to implement H, and then the drinking problem is solved on top of it.

To solve the dining philosopher’s problem:

A fork is either clean or dirty. A fork being used to eat with is dirty and remains dirty until it is cleaned. A clean fork remains clean until it is used for eating. A philosopher cleans a fork when mailing it (he is hygienic). A fork is cleaned only when it is mailed. An eat ing philosopher does not satisfy requests for forks until he has finished eating. The key issue is: which requests should a non-eating philosopher defer? In our algorithm, a non-eating philosopher defers requests for forks that are clean and satisfies requests for forks that are dirty.

And this turns out to be a model that we can use to implement H:

The direction of an edge between two neighbors u and v is from u to v (i.e., u has precedence over v) if and only if (1) u holds the fork shared by u and v, and the fork is clean, or (2) v holds the fork, and the fork is dirty, or (3) the fork is in transit from v to u. Observe that the direction (from u to v) of the edge can change only when u starts eating. Furthermore, all edges incident on an eating philosopher are directed toward it. Hence we have an implementation of the acyclicity rule: The direction of edges incident on a process may be changed only in the following way–all edges incident on a process may be simultaneously directed toward it.

We start out with all forks dirty and located at philosophers in such a way that H is acyclic.

Now we’re on the home straight. To solve the drinking philosopher’s problem, we allow philosophers to eat and drink:

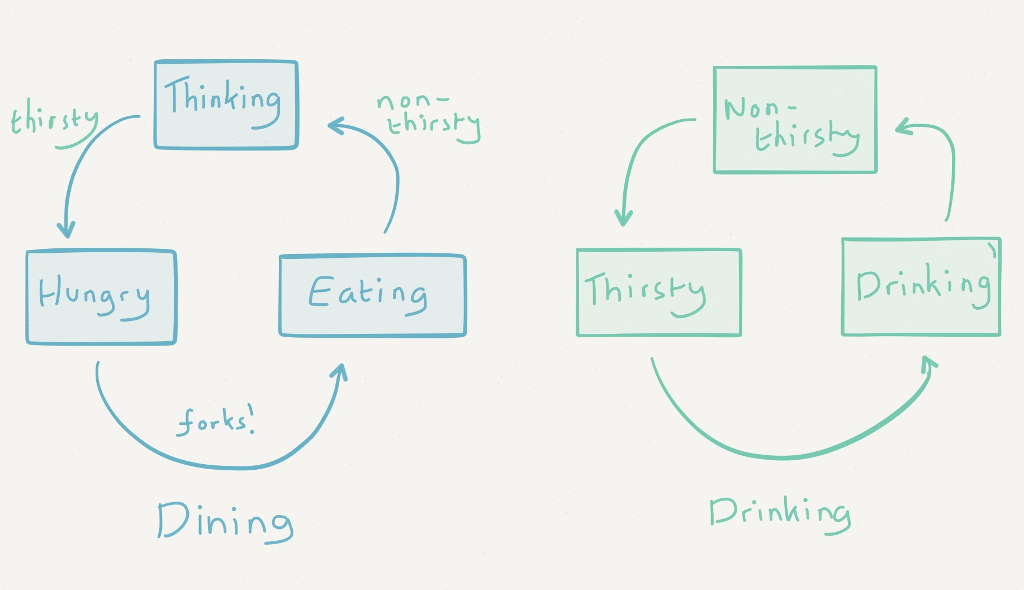
Forks are auxiliary resources in the sense that their sole purpose is to implement precedence graph H. Forks are not part of the drinkers problem specification; they are par t of the solution. The real resources in the drinkers problem are bottles. Our philosophers can eat and drink simultaneously, and we emphasize that eating is an artifact of our solution, used only to guarantee fair drinking. In our solution, the state of a philosopher is a pair (diner’s state, drinker’s state), where a diner’s state is one of thinking, hungry, or eating and a drinker’s state is one of tranquil, thirsty, or drinking.

Since the drinking characteristics of philosophers are defined by the problem, all that remains is to specify the dining characteristics. When a philosopher holds all the forks he or she needs, the philosopher transitions from hungry to eating. But when should a philosopher transition from thinking to hungry, and from eating to thinking? Three rules complete the puzzle:

1. A thinking, thirsty philosopher becomes hungry.
2. An eating, non-thirsty philosopher starts thinking.
3. “Philosopher u sends a bottle to philosopher v, in response to a request from v, if and only if u does not need the bottle or [u is not drinking and does not hold the fork for the edge (u, v)]. “

The basic idea is this: Suppose u has precedence over v (i.e., (u, v) is an edge in H) , but v holds the fork (i.e., the fork is dirty), and suppose u requests a bottle held by v. We require that u not only request the bottle held by v, but that u also request the fork. We show (from the solution to the diners problem) that in finite time v will yield the fork to u after which it must also yield the bottle to u. Thus, the algorithm ensures that if u has precedence over v in H then eventually the conflict resolution rule causes conflicts for bottles between u and v to be resolved in u’s favor.

If that’s not all crystal clear, perhaps it might be a good idea to grab a drink and think it over ;).