Relational inductive biases, deep learning, and graph networks

Relational inductive biases, deep learning, and graph networks Battaglia et al., arXiv’18

Earlier this week we saw the argument that causal reasoning (where most of the interesting questions lie!) requires more than just associational machine learning. Structural causal models have at their core a graph of entities and relationships between them. Today we’ll be looking at a position paper with a wide team of authors from DeepMind, Google Brain, MIT, and the University of Edinburgh, which also makes the case for graph networks as a foundational building block of the next generation of AI. In other words, bringing back and re-integrating some of the techniques from the AI toolbox that were prevalent when resources were more limited.

We argue that combinatorial generalization must be a top priority for AI to achieve human-like abilities, and that structured representation and computations are key to realizing this objective… We explore how using relational inductive biases within deep learning architectures can facilitate learning about entities, relations, and the rules for composing them.

Relational reasoning and structured approaches

Human’s represent complex systems as compositions of entities and their interactions. We use hierarchies to abstract away fine-grained differences, manage part-whole associations and other more general relationships, and can solve problems by composing familiar skills and routines.

… the world is compositional, or at least, we understand it in compositional terms. When learning, we either fit new knowledge into our existing structured representations, or adjust the structure itself to better accommodate (and make use of ) the new and the old.

Modern deep learning methods have done incredibly well following an end-to-end design philosophy that avoids explicit structure and ‘hand-engineering’. Such an approach seems to be finding its limits when it comes to challenges such as complex language and scene understanding, reasoning about structured data, transferring learning, and learning from small amounts of experience.

Instead of choosing between nature (end-to-end) and nurture (hand-engineering), can we use them jointly just as nature does, to build wholes greater that the sum of their parts?

A structured representation captures a composition of known building blocks, with structured computations operating over the elements and their composition as a whole. Relational reasoning operates over structure representations combining entities and relations, using rules for how they can be composed.

Recently, a class of models has arisen at the intersection of deep learning and structured approaches, which focuses on approaches for reasoning about explicitly structured data, in particular graphs…. What these approaches all have in common is a capacity for performing computation over discrete entities and the relations between them. What sets them apart from classical approaches is how the representations and the structure of the entities and relations — and the corresponding computations — can be learned, relieving the burden of needing to specify them in advance.

Relational inductive biases and graphs

We need some way of guiding a learning algorithm towards good solutions. The fancy term for this is inductive bias, the bias part being how an algorithm prioritises one solution over another, independent of the observed data. A regularization term is a form of inductive bias for example.

A relational inductive bias imposes constraints on relationships and interactions among entities in a learning process. Viewed through a relational lens, we can see relational inductive biases at work in several of the standard deep learning building blocks. We just need to uncover in each what are the entities, what are the relations, and what are the rules for composing them.

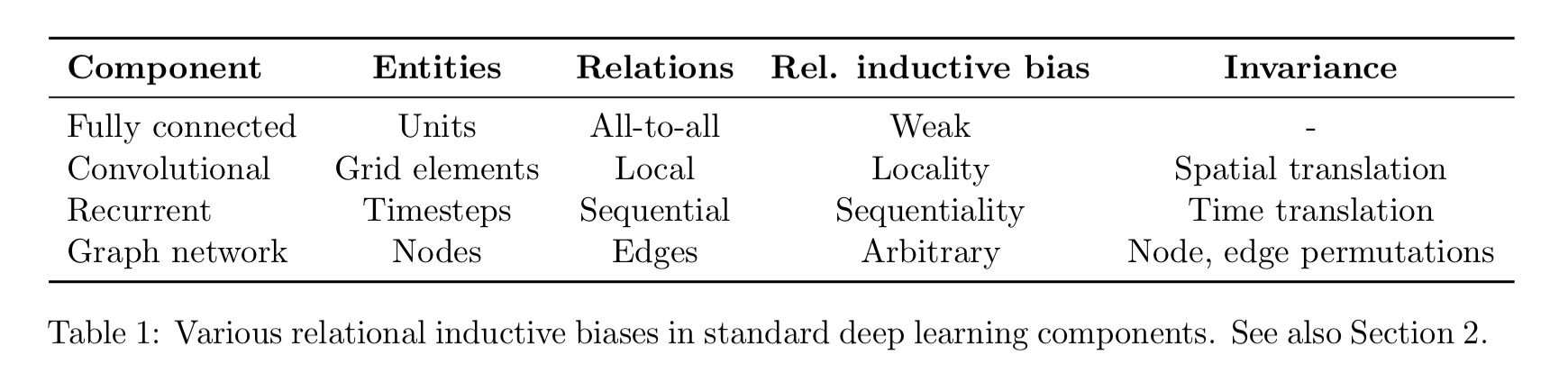
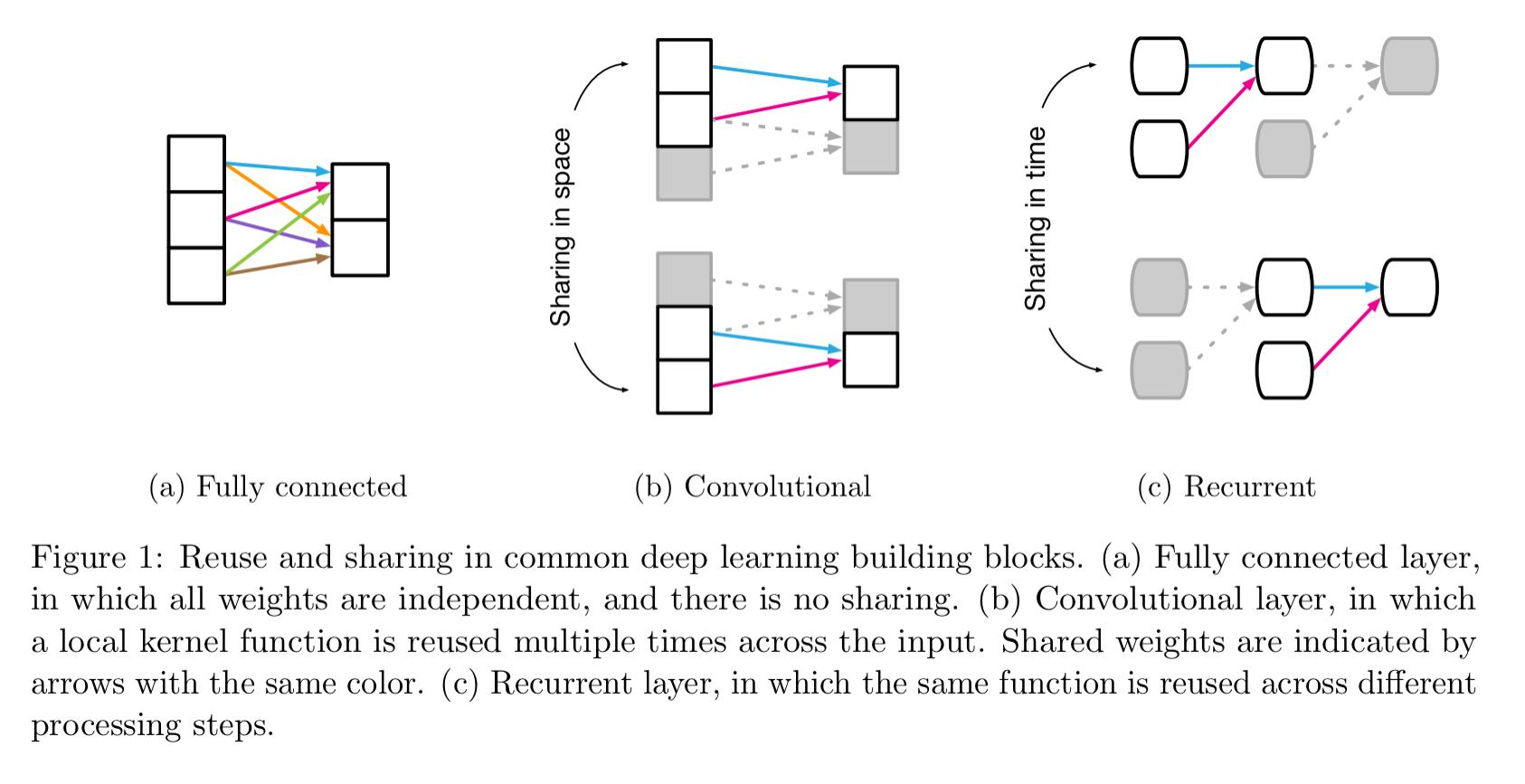
As an example, in a fully connected layer the entities are the units in the network, the relations are all-to-all, and the rules are specified by the weights and biases. “The implicit relational inductive bias in a fully connected layer is thus very weak: all input units can interact to determine any output unit’s value, independently across outputs.”

Within the building blocks we also see aspects of sharing (e.g. using a local kernel function across all inputs in a convolutional layer) and locality.

While the standard deep learning toolkit contains methods with various forms of relational inductive biases, there is no “default” deep learning component which operates on arbitrary relational structure. We need models with explicit representations of entities and relations, and learning algorithms which find rules for computing their interactions, as well as ways of grounding them in data.

A natural structure for this representation is a graph. Graphs support arbitrary (pairwise) relational structure, and computations over graphs afford a strong relational inductive bias. Many problems are easily modelled using a graph representation. For example:

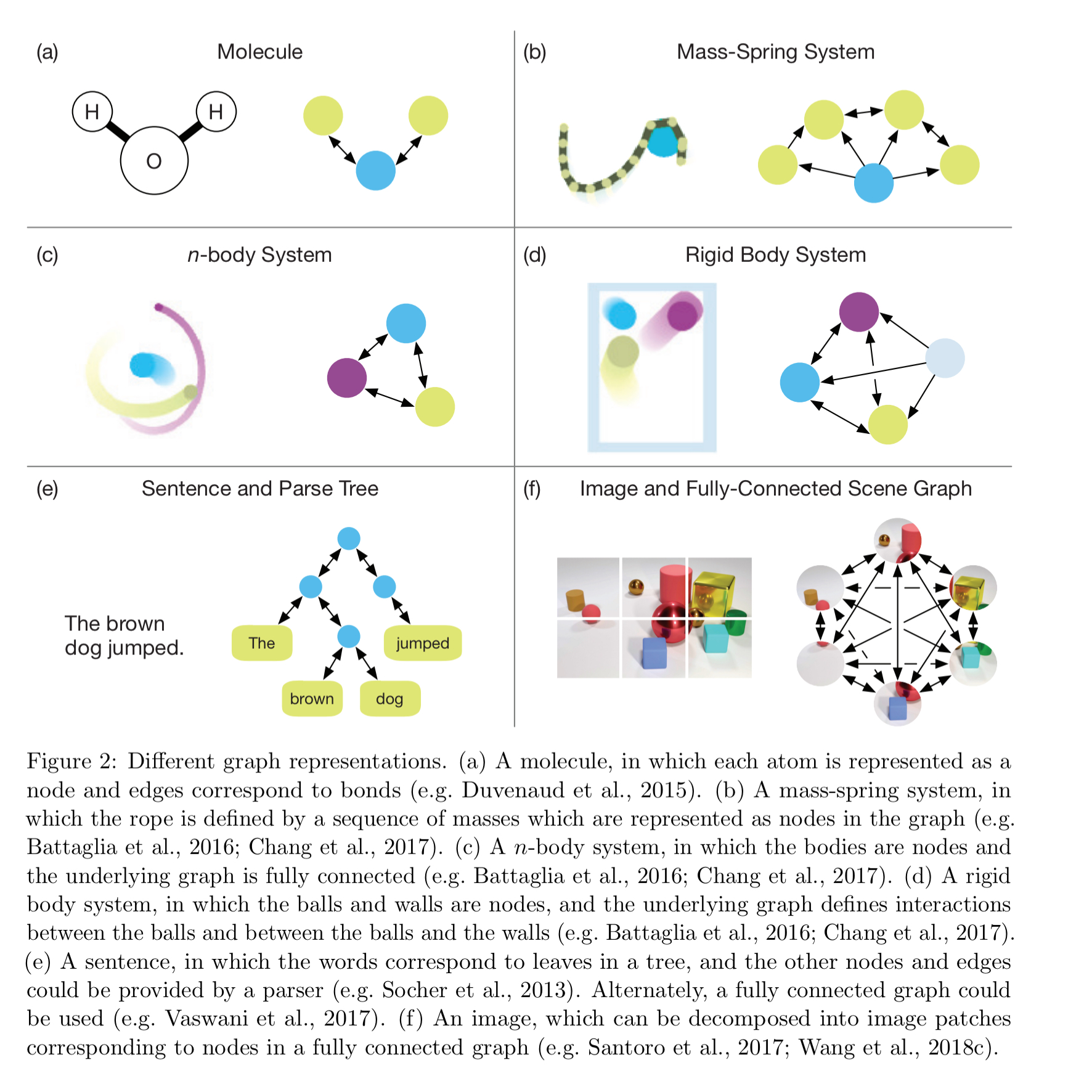
Introducing graph networks

There is a rich body of work on graph neural networks (see e.g. Bronstein et al. 2017) for a recent survey. Gilmer et al. introduced the message-passing neural network (MPNN) which unifies various graph neural network and graph convolutional approaches. Wang et al. introduced non-local neural networks (NLNN) unifying various ‘self-attention’ style methods. The graph network (GN) framework outlined in this paper generalises and extends graph neural networks, MPNNs, and NLNNs.

The main unit of computation in the GN framework is the GN block, a “graph-to-graph” module which takes a graph as input, performs computations over the structure, and returns a graph as output… entities are represented by the graph’s nodes, relations by the edges, and system-level properties by global attributes.

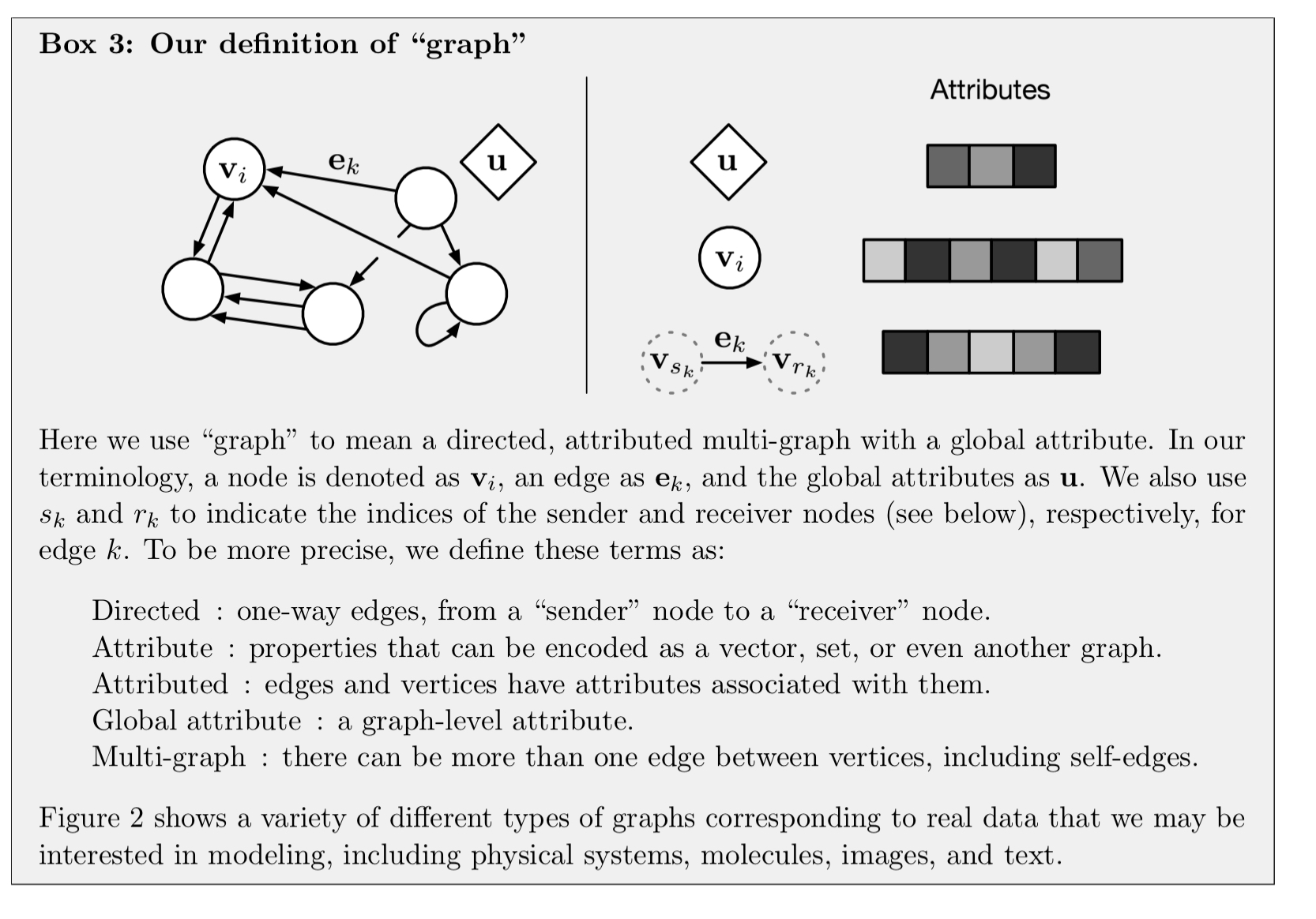
A graph is thus a three-tuple $G = (\mathbf{u}, V, E)$ where $\mathbf{u}$ is a global attribute, V is a set of nodes (each represented by attributes), and E is a set of edges (also represented by attributes).

GN blocks have three update functions $\phi$ and three aggregation functions $\rho$ .

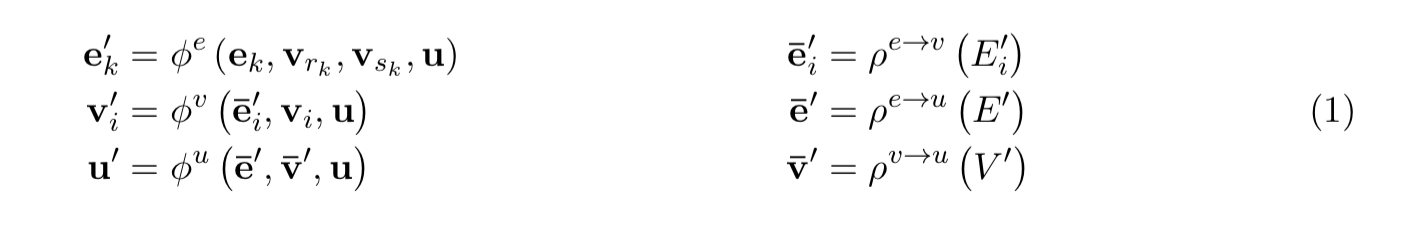
$\phi^{e}$ is mapped across all edges to compute per-edge updates, and then the $\rho^{e \mapsto v}$ function reduces the edge states to a single value $\mathbf{\bar{e}'}$ for each node. $\phi^{v}$ is then mapped across all nodes and $\rho^{e \mapsto u}$ reduces the node states to a single value. Finally the global attributed is update using $\phi^{u}$ and $\rho^{v \mapsto u}$ . The $\rho$ functions must be invariant to permutations of their inputs, and should take variable numbers of arguments (e.g., elementwise summation, mean, max etc.). Computations proceed from the edge, to the node, to the global level.

The full update algorithm is given below.

Consider an example graph where nodes represent rubber balls and edges are springs connecting them. We want to predict the movements of the balls in an arbitrary gravitational field.

The edge update step might compute the forces or potential energies between two connected balls.
The edge reduction step might sum all the forces or potential energies acting on the ith ball.
The node update step might compute the update position, velocity, and kinetic energy (attributes) of each ball.
The node reduction step aggregates all of the edge updates into a node, for example computing the summed forces (which should be zero in this case).
The global reduction step might then compute the total kinetic energy of the system
The global update step might compute something analogous to the net forces and total energy of the physical system.

Other update orders are possible (e.g. from global to node to edges).

Graph networks have (at least) three properties of interest:

The nodes and the edges between provide strong relational inductive biases (e.g. the absence of an edge between two nodes means that they should not directly influence each other).
Entities and relations are represented as sets, and thus are invariant to ordering and permutations. This is a desirable property in many contexts (e.g. objects in a scene do not have a natural ordering).
Since the per-edge and per-node functions are reused across all edges and nodes respectively, GNs automatically support a form of combinatorial generalisation. A single GN can operate on graphs of different sizes and shapes.

Graph network architectures

So far it seems like we’ve just been re-inventing a general graph computation framework. And indeed the framework is agnostic to specific representations and functional forms. But the fun stuff starts when we focus on deep learning architectures allowing GNs to act as learnable graph-to-graph function approximators. The three design principles behind graph networks which support this are:

flexible representations
configurable within-block structure, and;
composable multi-block architectures

Flexible representations refers to the choice of representation for the attributes of edges, nodes, and global state, as well as the form of the outputs. For deep learning implementations, real-valued vectors and tensors would be a likely choice. Edge and node outputs would typically correspond to lists of vectors or tensors, and global outputs to a single vector or tensor. Thus the output of a GN block can be passed to other deep learning building blocks. The relational structure (the graph) can be explicitly specified in the inputs, or it can be inferred or assumed.

Configurable within-block structure refers to flexibility in how the internal structure and functions of a GN block are configured. The $\phi$ functions could themselves be implemented as neural networks for example (e.g. MLPs for vectors, or CNNs for tensors). There are GN configurations that correspond to many existing works in the literature. The following figure shows some examples.

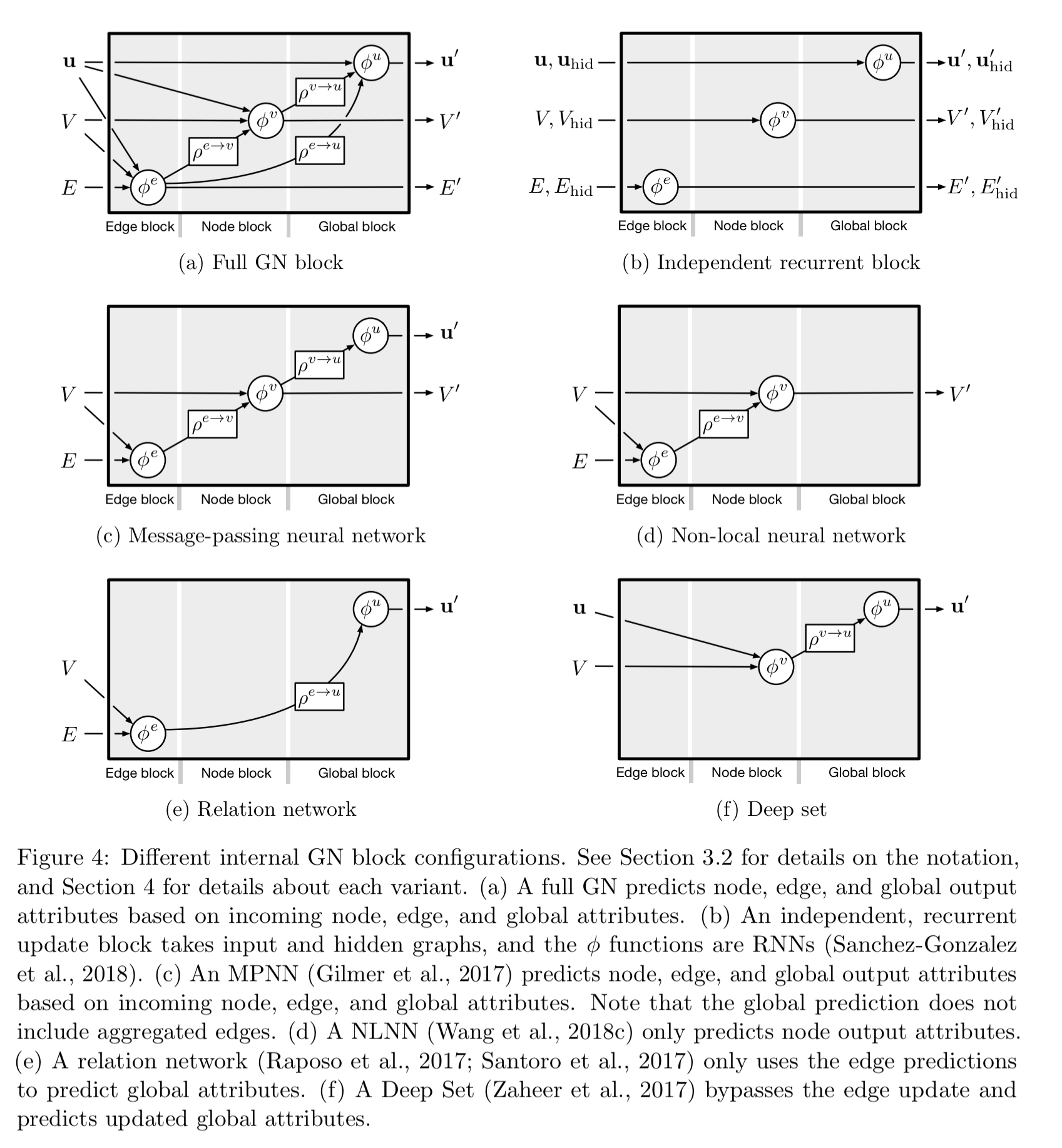
Composable multi-block architectures refers to the fact that the output of one GN block can be fed into another GN block as an input. In general arbitrary numbers of GN blocks can be composed.

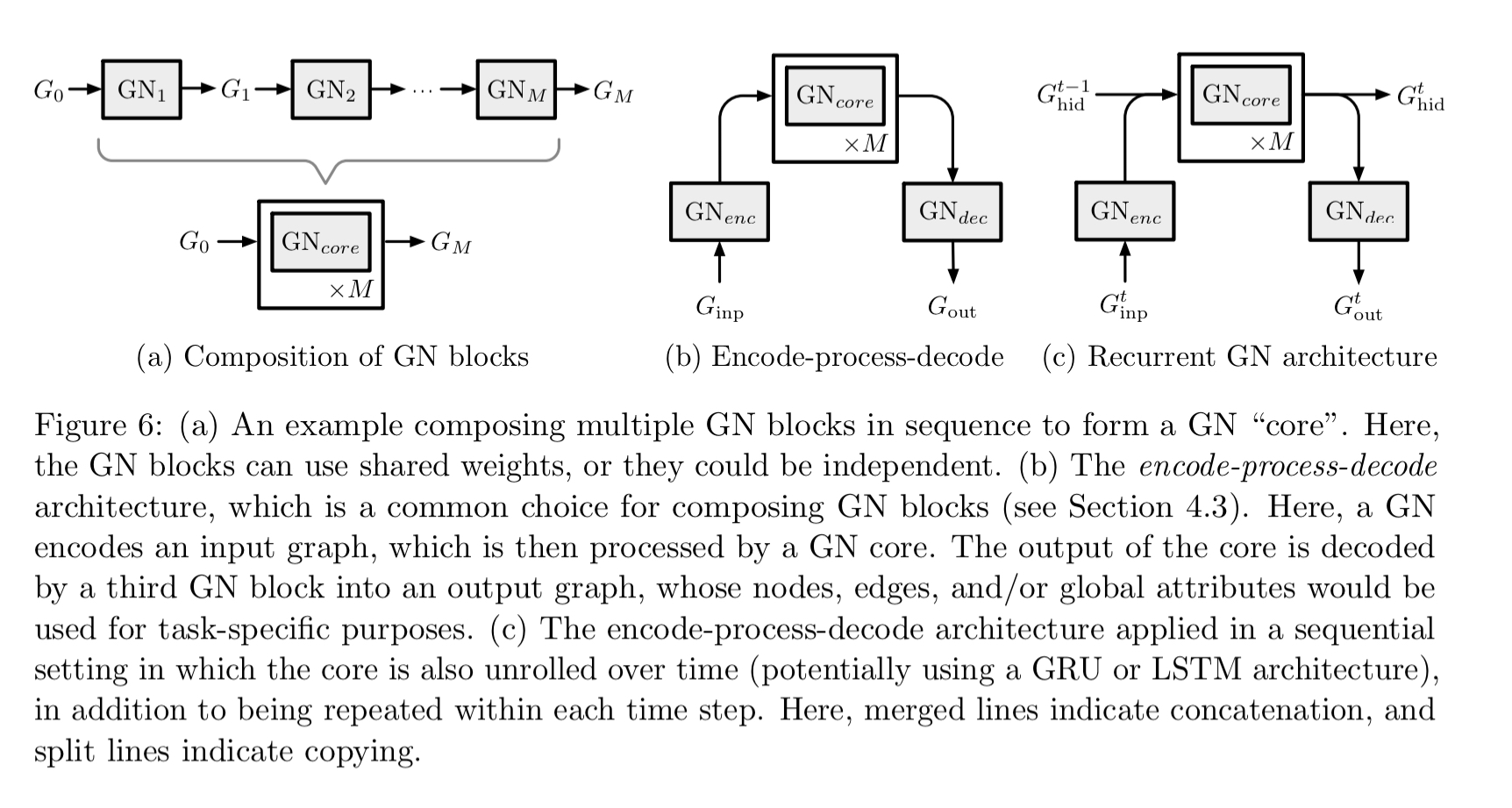
One common design is the encode-process-decode configuration in which an input graph is transformed into a latent representation by an encoder GN, a shared core block is applied multiple times to process the encoding, and then a decoder GN produces the final output.

What’s next

Realizing the full potential of graph networks will likely be far more challenging than organizing their behaviour under one framework, and indeed, there are a number of unanswered questions regarding the best ways to use graph networks. One pressing question is: where do the graphs come from that the graph networks operate over?

For example, how should we convert raw sensory data into structured graph representations?

And beyond just graphs, “one takeaway from this paper is less about graphs themselves and more about the approach of blending powerful deep learning approaches with structured representations.”

… learnable models which operate on graphs are only a stepping stone on the path toward human-like intelligence. We are optimistic about a number of other relevant, and perhaps underappreciated, research directions, including marrying learning-based approaches with programs, developing model-based approaches with an emphasis on abstraction, investing more heavily in meta-learning, and exploring multi-agent learning and interaction as a key catalyst for advanced intelligence.

The authors state an intention to release an open-source implementation for graph networks later this year.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic