Same-different problems strain convolutional neural networks Ricci et al., arXiv 2018
Since we’ve been looking at the idea of adding structured representations and relational reasoning to deep learning systems, I thought it would be interesting to finish off the week with an example of a problem that seems to require it: detecting whether objects in a scene are the same or different.
This image containing a flute was correctly classified by a CNN trained on millions of photographs. On ImageNet the network even surpassed the accuracy of a human observer.

This image contains two shapes that are the same, a relationship that is immediately obvious to a human observer. “Yet, the CNN failed to learn this relation even after seeing millions of training examples.”
The above is an example of a same-different (SD) visual relation problem (output whether the objects in the scene are the same, or different). Spatial relation (SR) problems ask whether objects follow a certain spatial relation, e.g. in a line, horizontally stacked, vertically stacked, and so on. For example:
The synthetic visual reasoning test (SVRT) contains a collection of 23 binary classification problems along these lines. In each case opposing classes differ based on whether their stimuli obey an abstract rule. If you train a bunch of CNNs (with different depths, filter sizes, etc.) on these tasks an interesting pattern pops out. The CNNs really struggled on problems where the abstract rule required detecting whether things were the same or different (congruent up to some transformation), whereas they achieved good accuracy on spatial relation problems.
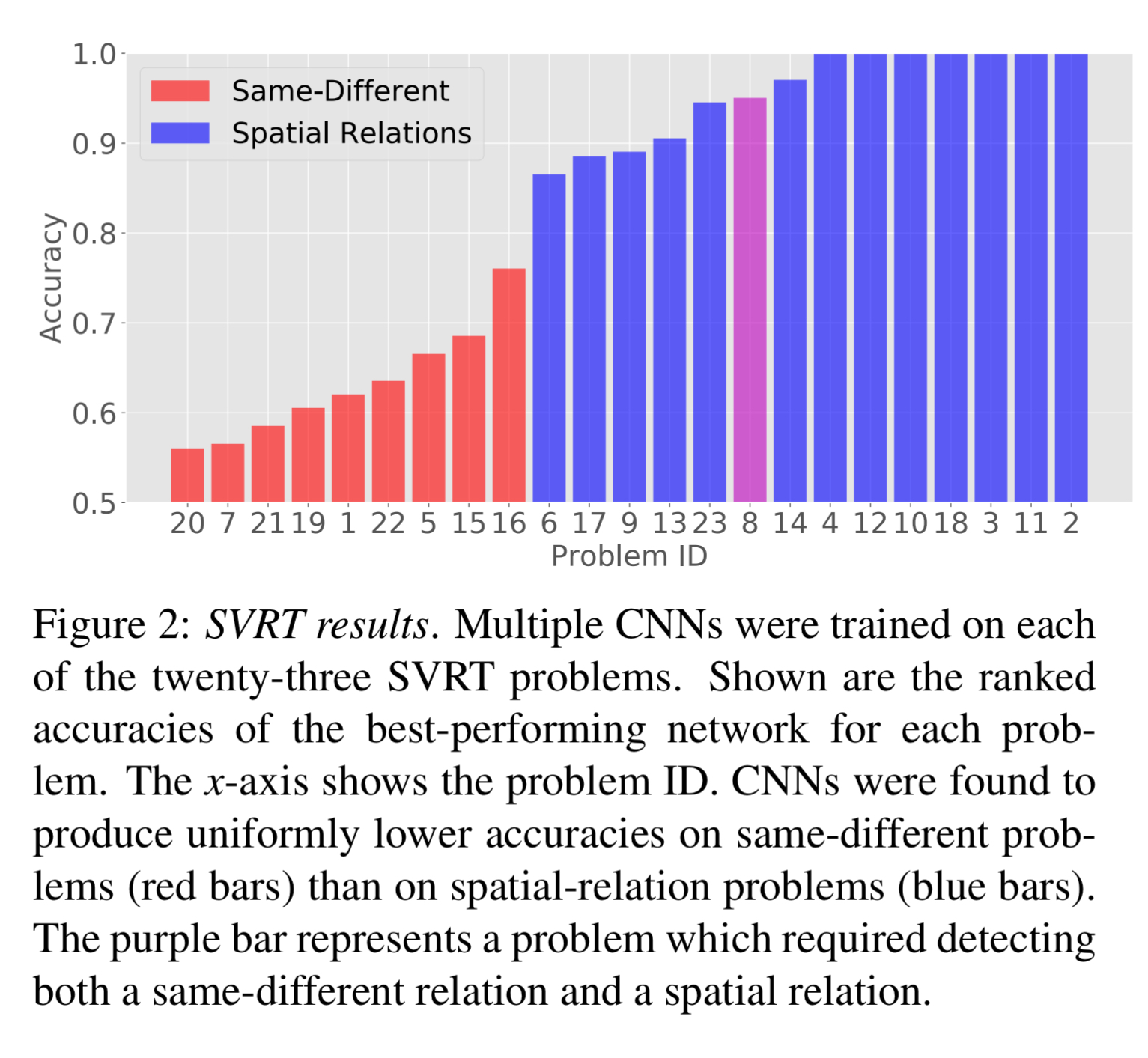
The resulting dichotomy across the SVRT problems is striking. CNNs fare uniformly worse on SD problems than they do on SR problems. Many SR problems were learned satisfactorily, whereas some SD problems (e.g. problems 20 and 7) resulted in accuracy not substantially above chance.
For SR problems, all the CNNs did pretty well, regardless of network configuration. But for SD problems larger networks performed noticeably better than smaller ones. This suggests that something about the SD problems is straining the capacity of the CNNs.
Probing further
To dig deeper into this apparent difference between same-different and spatial-relation problems the authors construct a new visual-relation benchmark called PSVRT. The dataset is parameterised so that the size of the items in the scene, the number of scene items, and the size of the whole image can all be controlled. Scene items are just binary bit patterns placed on a blank background. For any given configuration of parameters, the resulting scene can be used for both an SD problem and an SR problem, simply based on labelling.

Our goal was to examine how hard it is for a CNN architecture to learn relations for visually different but conceptually equivalent problems. If CNNs can truly learn the “rule” underlying these problems, then one would expect the models to learn all problems with more-or-less equal ease. However, if the CNN only memorize the distinguishing features of the two image classes, then learning should be affected by the variability of the example images in each category.
A baseline architecture was established with four convolutional layers, that was able to easily learn both the same-different and spatial-relation PSVRT problems with item size 4, image size 60, and two items in the image. This baseline CNN was then trained from scratch on a variety of PSVRT problems, each time using 20 million training images and a batch size of 50. There were three sub-experiments:
- Fixing item size (m) at 4, number of items (k) at 2, and varying image size (n) between 30 and 180.
- Fixing image size at 60, number of items at 2, and varying item size between 3 and 7.
- Fixing image size at 60, item size at 4, and varying the number of items between 2 and 6.
In all conditions, we found a strong dichotomy between SD and SR conditions. In SR, across all image parameters and in all trials, the model immediately learned at the start of training and quickly approached 100% accuracy, producing consistently high and flat mean ALC curves. In SD, however, we found that the overall ALC was significantly lower than SR.
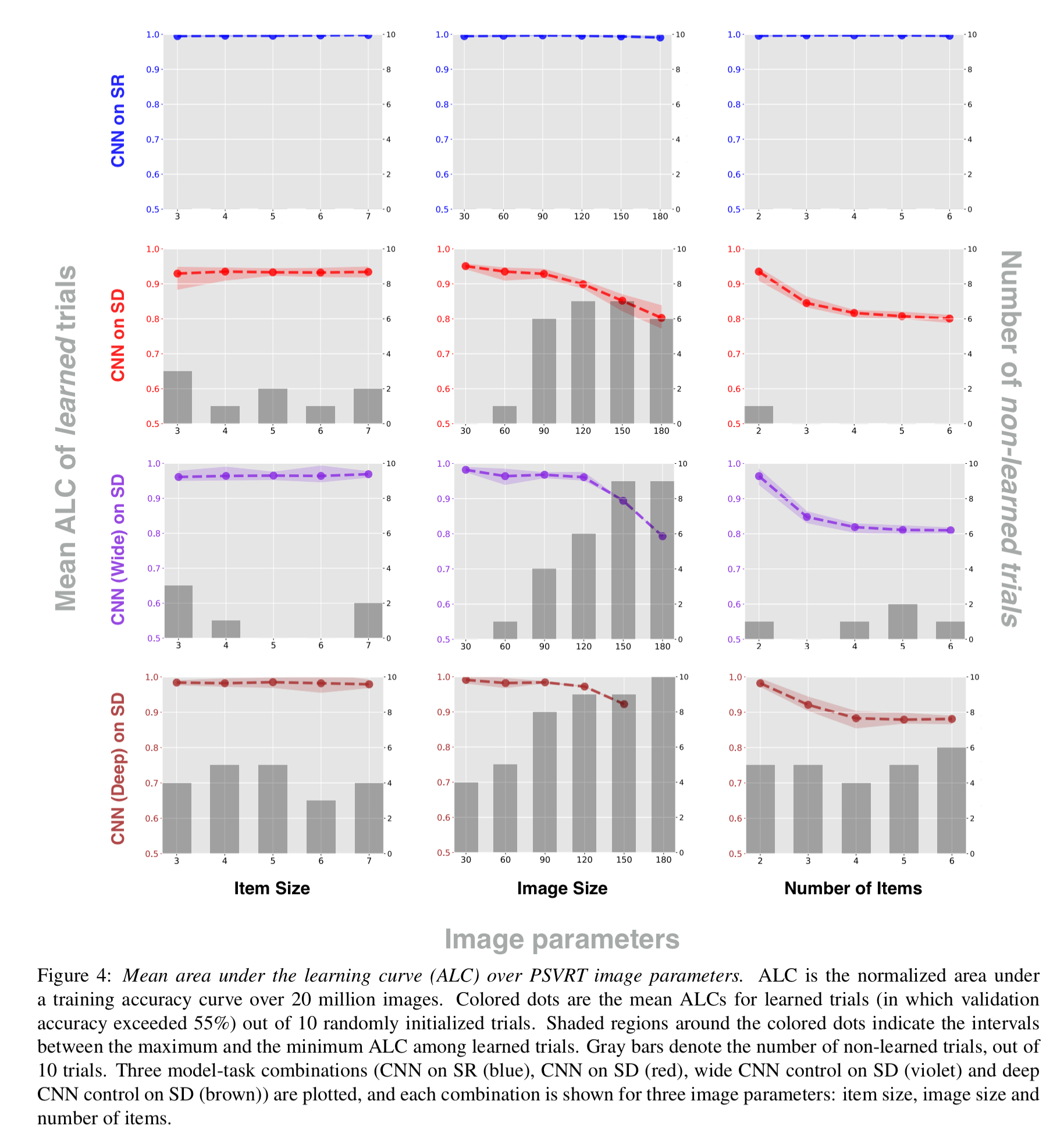
Digging deeper, when learning did occur in SD, increasing item size never strained performance. But increasing the overall image size, or increasing the number of items did. (Gray bars in the above figures indicate the number of trials in which learning failed). The results suggest that straining is not simply a direct outcome of an increase in image variability. Using CNNs with more than twice the number of kernels (wide), or twice as many layers (deep) did not change the observed trend.
What’s going on?
The authors hypothesise that the CNNs learn ‘subtraction templates’ when tackling SD problems: filters with one positive region and one negative region. Each relative arrangement of items requires a different subtraction template since each item must lie in on of the template’s two regions. If identical items lie in opposing regions, they are subtracted by the synaptic weights. The difference is used to choose the appropriate same/different label.
A strategy like this doesn’t require memorizing specific items, so item size doesn’t make much of a difference. However, image size (the biggest straining factor) exponentially increases the possible number of arrangements of items.
Our results indicate that visual-relation problems can quickly exceed the representational capacity of feedforward networks. While learning templates for individual objects appears to be tractable for today’s deep networks, learning templates for arrangements of objects becomes rapidly intractable because of the combinatorial explosion in the number of features to be stored… Given the vast superiority of humans over modern computers in their ability to detect visual relations, we see the exploration of attentional and grouping mechanisms as an important next step in our computational understanding of visual reasoning.