Continuing our tour through some of the ‘top 100 awesome deep learning papers,’ today we’re turning our attention to the unsupervised learning and generative networks section. I’ve split the papers here into two groups. Today we’ll be looking at:
- Building high-level features using large-scale unsupervised learning, Le et al., 2012
- Generative Adversarial Nets, Goodfellow et al., 2014
- Unsupervised representation learning with deep convolutional generative adversarial networks, Radford et al., 2015
- Improved techniques for training GANs, Salimans et al., 2016
Building high-level features using large-scale unsupervised learning
This is a fascinating paper. Consider an unsupervised learning scenario in which a deep autoencoder is fed a large number of images (the authors construct a training dataset by sampling frames from 10 million YouTube videos). Do the features learned by the encoder correspond in any way to the things that you and I might recognise as features? And are there even neurons that specialise for recognising certain types of object? If so, that would not only be really interesting in and of itself, but we could also figure out which objects fire in response to which objects, and so build a classifier.
This work investigates the feasibility of building high-level features from only unlabeled data. A positive answer to this question will give rise to two significant results. Practically, this provides an inexpensive way to develop features from unlabeled data. But perhaps more importantly, it answers an intriguing question as to whether the specificity of the “grandmother neuron” could possibly be learned from unlabeled data. Informally, this would suggest that it is at least in principle possible that a baby learns to group faces into one class because it has seen many of them and not because it is guided by supervision or rewards.
After training, the authors use a test set of 37,000 images sampled from the ‘Labeled faces in the Wild’ dataset and from ImageNet. These images are fed to the encoder, and the performance of each output neuron in classifying faces is measured…
Surprisingly, the best neuron in the network performs very well in recognizing faces, despite the fact that no supervisory signals were given during training. The best neuron in the network achieves 81.7% accuracy in detecting faces.
It’s worth letting that sink in for a moment – just by repeatedly showing the network bunches of pixels, it has learned to encode a feature that represents the pattern of a face, without ever even knowing that there is such a thing as a face a priori.
Here are the 48 test images that most strongly stimulate the ‘face’ neuron:

Definitely faces!
And somewhat creepily, here’s the ghost face that emerges when searching for the input that maximizes the firing of the neuron:

The neuron also turns out to be robust against ‘complex and difficult to hard-wire’ invariances such as out-of-phase rotation and scaling.
Having achieved a face-sensitive neuron, we would like to understand if the network is also able to detect other high-level concepts. For instance, cats and body parts are quite common in YouTube. Did the network also
learn these concepts?
A question of central importance to the Internet I’m sure you’ll agree, ‘is there a cat neuron, and if so what does the prototypical cat look like?’ And yes, there is a learned cat neuron, and there is a human body neuron too! Although the maximal stimulation ghost images aren’t as impressive as the face one. The human body shape you can just about make out. The cat face I swear I could see at one point, but as of this time of writing it’s gone again! A bit like one of those optical illusions you have to stare at until you suddenly ‘see’ it.
If you take a trained encoder and add a one-vs-all logistic classifier on top of the highest layer of the network, you have yourself a classifier…
Generative adversarial nets (GANs)
So far, the most striking successes in deep learning have involved discriminative models, usually those that map a high-dimensional, rich sensory input to a class label. These striking successes have primarily been based on the backpropagation and dropout algorithms, using piecewise linear units which have a particularly well-behaved gradient . Deep generative models have had less of an impact, due to the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies, and due to difficulty of leveraging the benefits of piecewise linear units in the generative context. We propose a new generative model estimation procedure that sidesteps these difficulties.
The core idea is simple to understand (the theoretical results showing why it works, a little less so!). Take a generator model G that generates (for example) images from noise. Pit it against a discriminator model D whose task it is to classify the image as either coming from the generator, or from the real data distribution.
The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency. Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles.
If the generative model and discriminative model are both multilayer perceptrons then both models can be trained using backpropagation and dropout. This special case is termed adversarial nets. We are searching for a solution where G recovers the training data distribution, and D is equal to 1/2 everywhere. Training alternates between k steps of optimizing D, and one step of optimizing G. “This results in D being maintained near its optimal solution, so long as G changes slowly enough.”
We want to learn the generator’s distribution over data
. Given input noise variables
, let
be a differential function representation by a multilayer perceptron, with parameters
. Let
be a second multilayer perceptron outputting a single scalar representing the probability that
came from the data rather than from
.
We train D to maximize the probability of assigning the correct label to both training examples and samples from G. We simultaneously train G to minimize log(1 – D(G(z)).
Below are examples of samples generated using this technique from the MNIST and TFD datasets. The rightmost column is the nearest training example of the neighbouring sample.

Unsupervised representation learning with deep convolutional generative adversarial networks
In the first two papers we looked at unsupervised learning of image features and at GANs. Now we get to put the two together…
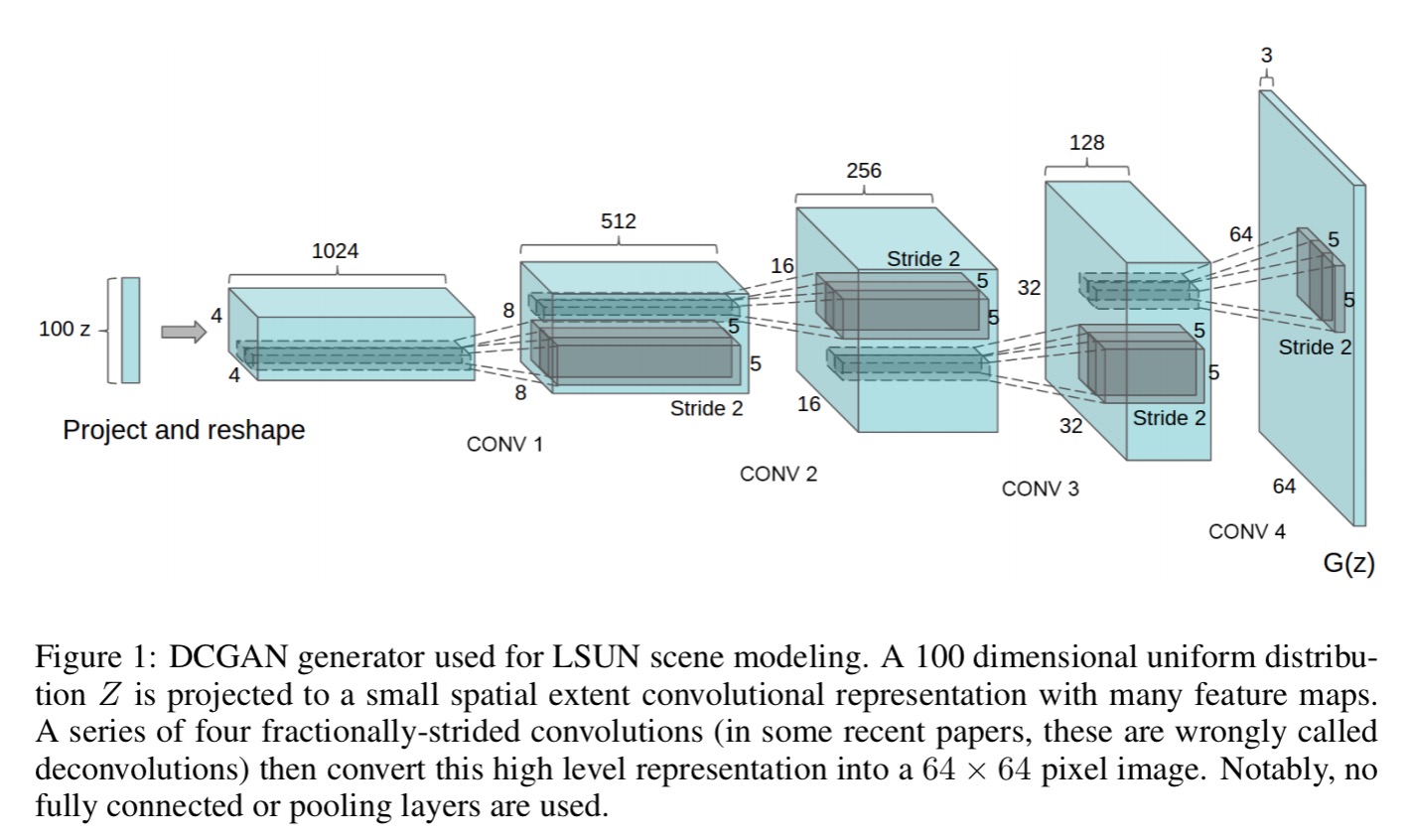
In this work, we hope to help bridge the gap between the success of CNNs for supervised learning and unsupervised learning. We introduce a class of CNNs called deep convolutional generative adversarial networks (DCGANs), that have certain architectural constraints, and show that they are a strong candidate for unsupervised learning.
If you recall the amazing vector manipulations we did with word embeddings, such as King – Man + Woman = Queen, then you’re in for a real treat when we get to do similar arithmetic with vectors representing visual concepts.
Here’s the core idea: we can train a GAN (unsupervised learning), which must somewhere internally encode representations useful for images, and then reuse parts of the generator and discriminator networks as feature extractors for supervised tasks.
There’s a small catch though, previous attempts to scale up GANs using CNNs met with limited success, often being unstable to train and resulting in generators that produce nonsensical outputs.
… after extensive model exploration we identified a family of architectures that resulted in stable training across a range of datasets and allowed for training higher resolution and deeper generative models.
Here are the guidelines for training DCGANs:
- Replace any pooling layers with strided convolutions – this allows the network to learn its own spatial downsampling.
- Remove any fully connected hidden layers on top of convolutional features. The authors found that connecting the highest convolutional features to the input and output respectively of the generator and discriminator worked well.
- Use batch normalization, which stabilizes learning by normalizing the input to each unit to have zero mean and unit variance.
- Use ReLU activation for all generator layers, except for the final output layer where tanh works better
- Use Leaky ReLU activation for all discriminator layers. (We can update that advice to PReLUs now).
DCGANs were trained on the Large-scene understanding (LSUN), ImageNet-1K and a Faces dataset. Here are examples of bedrooms generated after five epochs of training:

The discriminator network can then be used to build a supervised classifier:
To evaluate the quality of the representations learned by DCGANs for supervised tasks, we train on Imagenet-1k and then use the discriminator’s convolutional features from all layers, maxpooling each layers representation to produce a 4 × 4 spatial grid. These features are then flattened and concatenated to form a 28672 dimensional vector and a regularized linear L2-SVM classifier is trained on top of them. This achieves 82.8% accuracy, out performing all K-means based approaches.
Section 6 of the paper is the really fun part though. This is where the authors set out to investigate what kinds of features the network has learned.
If walking in the latent space results in semantic changes to the image generations (such as objects being added and removed), we can reason that the model has learned relevant and interesting representations…
And here a couple of compelling demonstrations that indicate this is indeed the case: a room without a window slowing being transformed into a room with a large window, and a TV slowly being transformed into a window.


We demonstrate that an unsupervised DCGAN trained on a large image dataset can also learn a hierarchy of features that are interesting. Using guided backpropagation as proposed by (Springenberg et al., 2014), we show in Fig.5 that the features learnt by the discriminator activate on typical parts of a bedroom, like beds and windows.

To see whether the generator learns specific object representations (as we saw in our first paper today) , the authors perform a similar analysis to find the neurons with the strongest activation in the presence of windows. Then random new samples are generated with (top row) and without (bottom row) these features included.

And now the moment you’ve been waiting for…
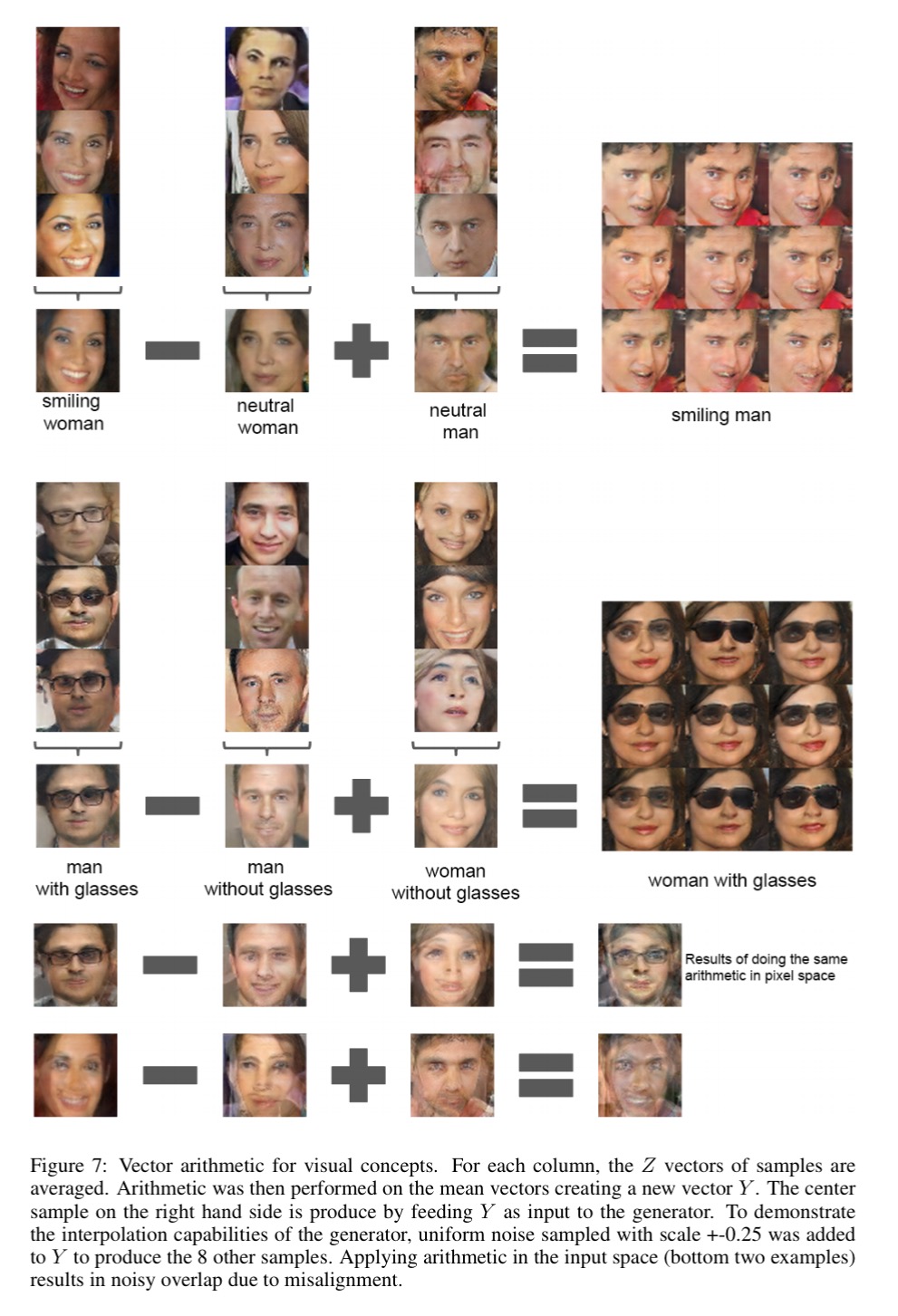
In the context of evaluating learned representations of words (Mikolov et al., 2013) demonstrated that simple arithmetic operations revealed rich linear structure in representation space. One canonical example demonstrated that the vector(”King”) – vector(”Man”) + vector(”Woman”) resulted in a vector whose nearest neighbor was the vector for Queen. We investigated whether similar structure emerges in the Z representation of our generators. We performed similar arithmetic on the Z vectors of sets of exemplar samples for visual concepts. Experiments working on only single samples per concept were unstable, but averaging the Z vector for three examplars showed consistent and stable generations that semantically obeyed the arithmetic.
In the picture below, the three top pictures in each column (Z vectors) were averaged to produce the picture (Z vector) you see below them, and then the vector operations were applied. The result is the center image in the box of nine that you see on the right-hand side, the other images surrounding it have small amounts of noise added.
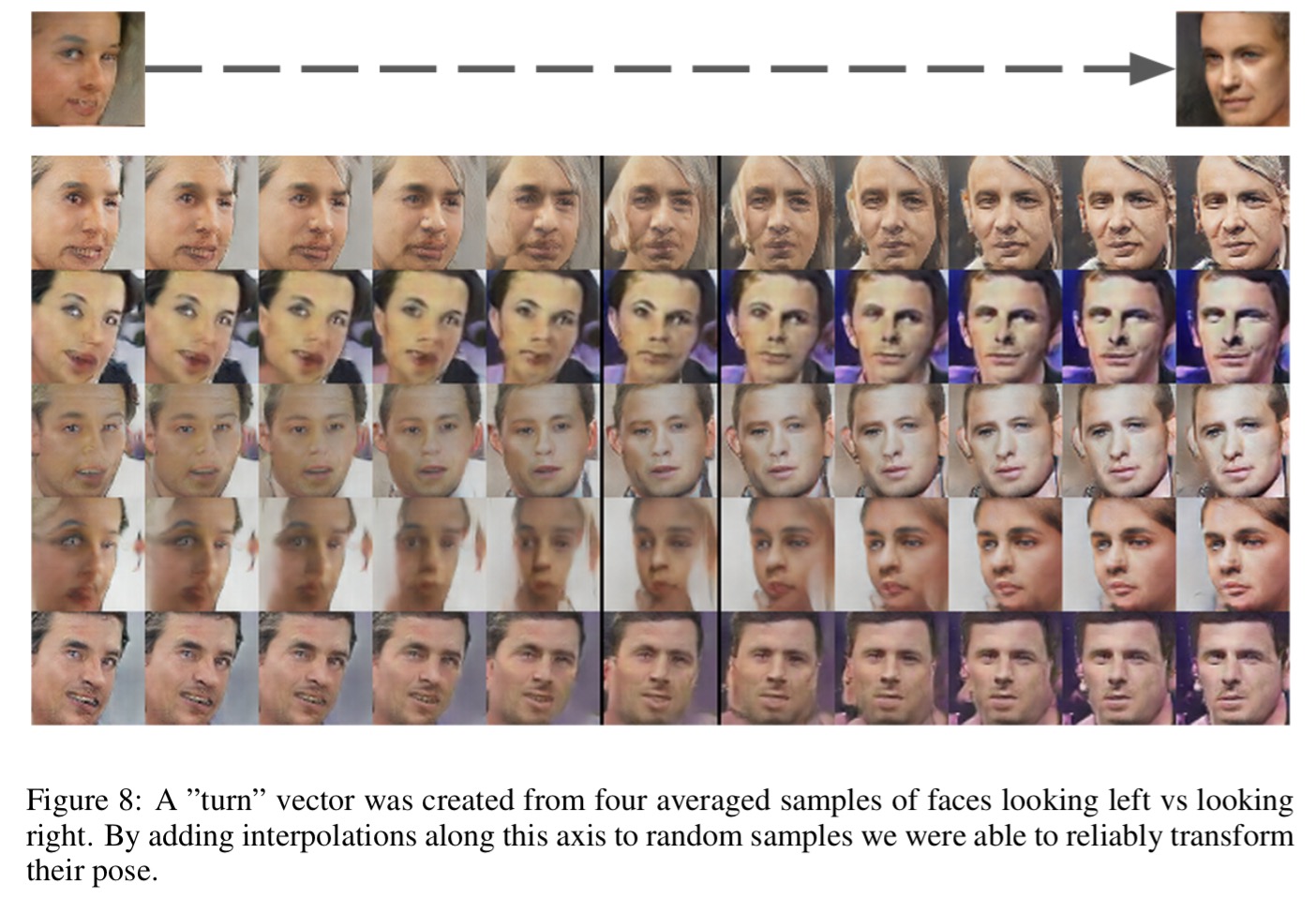
And if you’ll indulge me one more time, here’s the extraction of a ‘turn’ vector by differencing left-facing and right-facing faces. When you apply it to new face images, you can change the pose!
Improved techniques for training GANs
This paper focuses on the use of GANs for semi-supervised learning and image generation, but along the way (as the title suggests), it makes key contributions in two areas: how to efficiently train GANs, and how to evaluate the quality of generated images.
… training GANs requires finding a Nash equilibrium of a non-convex game with continuous, high-dimensional parameters. GANs are typically trained using gradient descent techniques that are designed to find a low value of a cost function, rather than to find the Nash equilibrium of a game. When used to seek for a Nash equilibrium, these algorithms may fail to converge.
There are five heuristics for improving training.
- Instead of directly maximising the output of the generator, require the generator to generate data matching the statistics of the real data. “Specifically, we train the generator to match the expected value of the features on an intermediate layer of the discriminator. This is a natural choice of statistics for the generator to match, since by training the discriminator we ask it to find those features that are most discriminative of real data versus data generated by the current model.” This process is called feature matching.
- Use mini-batching to look at multiple data examples in combination. This help to prevent the generator collapsing to a mode where it always emits the same point.
- Use historical averaging by adding a term to each player’s cost function that looks at the difference between the current parameter values and those over the last t time steps. ‘This approach is loosely inspired by the fictitious play algorithm that can find equilibria in other kinds of games.‘
- Use one-side label smoothing. This is the idea of replacing 0 and 1 targets for a classifier with smoothed values, as we saw with distillation. Best results are obtained when smoothing only positive labels, leaving negative labels set to zero (hence ‘one-sided’).
- Use virtual batch normalization. Chose a fixed reference set of examples at the start of training, and normalize this set using its own statistics. Then during training each example
is normalized based on the statistics from this reference batch.
Now we turn our attention to the question of how to figure out whether the generated images are any good.
Generative adversarial networks lack an objective function, which makes it difficult to compare performance of different models.
One option is to use human judges (e.g. via Amazon Mechanical Turk) – this is comparatively slow though, and its hard to get consistent ratings. Seeking an automatic method to evaluate samples, the authors apply the Inception model to every generated image to get the conditional label distribution . If the generated image contains meaningful objects, we should expect the label distribution to have low entropy (i.e., to show strong preference for one or a small number of class labels because it is something that the Inception network recognises). And since we also want the model to generate varied images, then looking at the label distributions across a whole set of images should show high entropy (i.e., the generated images contain a variety of different objects). These two requirements are combined to create the Inception Score metric.
Now that we can train GANs efficiently, and we know how to evaluate the generator, we can use GAN generators during semi-supervised learning. The generated images are used to extend the training dataset (e.g. 50% real images, and 50% generated). It works like this:
- Take any classifier, making predictions across K classes.
- Increase the dimension of the classifier output by one, to make K+1 dimensions, this new
generatedclass will represent generated images. is therefore the probability assigned to
being a generated image. This corresponds to
in the original GAN framework.
- We can now learn from both labeled and unlabeled data. Given unlabeled data we can use it for classifier training so long as the predicted class is not ‘
generated.’ - The loss function for training the classifier becomes
.
In practice, Lunsupervised will only help if it is not trivial to minimize for our classifier and we thus need to train G to approximate the data distribution. One way to do this is by training G to minimize the GAN game-value, using the discriminator D defined by our classifier. This approach introduces an interaction between G and our classifier that we do not fully understand yet, but empirically we find that optimizing G using feature matching GAN works very well for semi-supervised learning, while training G using GAN with minibatch discrimination does not work at all.
When used purely for image generation though, minibatch discrimination yields better results, as can be seen in these generated MNIST digits:
