Today we’re looking at the remaining papers from the unsupervised learning and generative networks section of the ‘top 100 awesome deep learning papers‘ collection. These are:
- DRAW: A recurrent neural network for image generation, Gregor et al., 2015
- Pixel recurrent neural networks, van den Oord et al., 2016
- Auto-encoding variational Bayes, Kingma & Welling, 2014
DRAW: A recurrent neural network for image generation
The networks we looked at yesterday generate a complete image all at once. This “one shot” approach is hard to scale to large images. If you ask a person to draw some visual scene, they will typically do so in a sequential iterative fashion, working from rough outlines to detail, first on one part, then on another.
The Deep Recurrent Attentive Writer (DRAW) architecture represents a shift towards a more natural form of image construction, in which parts of a scene are created independently from others, and approximate sketches are successively refined.
At its core, DRAW is a variational autoencoder (an autoencoder making use of variational inference techniques). The encoder and decoder however are both RNNs (LSTMs):
… a sequence of code samples is exchanged between them; moreover, the encoder is privy to the decoder’s previous outputs, allowing it to tailor the codes it sends according to the decoder’s behavior so far.
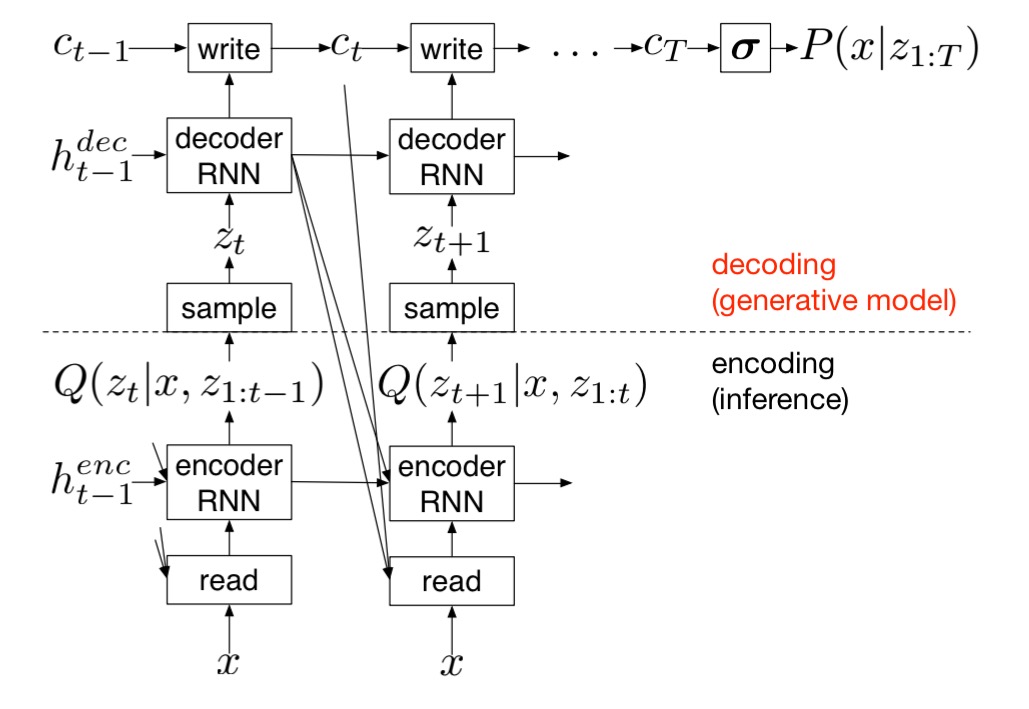
The decoder’s outputs are successively added to the distribution that will ultimately generate the data, as opposed to emitting it in a single step. This much takes care of the iterative part of human image construction. To model the phenomenon of working first on one part of the image, and then on another, an attention mechanism is used to restrict both the input region observed by the encoder, and the output region modified by the decoder.
In simple terms, the network decides at each time-step “where to read” and “where to write” as well as “what to write”.
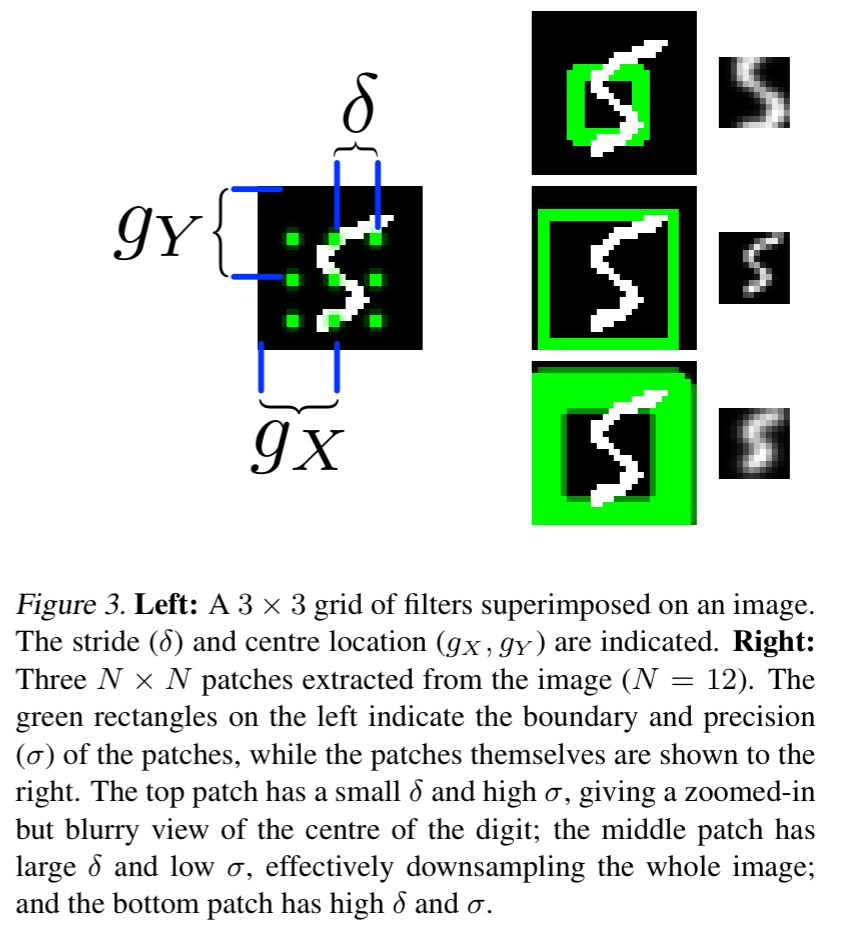
The attention mechanism resembles the selective read and write operations of the Neural Turing Machine that we looked at last year, however it works in 2D. An array of 2D Guassian filters is applied to the image, which yields image patches of smoothly varying location and zoom.
As illustrated [below], the N ×N grid of Gaussian filters is positioned on the image by specifying the co-ordinates of the grid centre and the stride distance between adjacent filters. The stride controls the ‘zoom’ of the patch; that is, the larger the stride, the larger an area of the original image will be visible in the attention patch, but the lower the effective resolution of the patch will be.
Once a DRAW network has been trained, an image can be generated by iteratively picking latent samples and running the decoder to update the canvas matrix. Here we can see how images evolve when a trained DRAW network generates MNIST digits:

The final generated digits are pretty much indistinguishable from the originals.

Here’s another set of generated images, this time from a network trained on a multi-digit Street View House Numbers dataset:

Pixel recurrent neural networks
In contrast to DRAW, Pixel RNNs use a distinctly un-human approach: they model the probability of raw pixel values. The goal of the work is to be able to model natural images on a large scale, but the authors also evaluated Pixel RNNs on good old MNIST, and reported the best result so far (including against DRAW). There are two variations of the basic idea in the paper, a full-fat Pixel RNN architecture, and a simpler Pixel CNN one – both are substantial.
A Pixel RNN network has up to twelve two-dimensional LSTM layers:
These layers use LSTM units in their state and adopt a convolution to compute at once all the states along one of the spatial dimensions of the data.
To generate pixel , Pixel conditions on all the previously generated pixels left and above it.
![]()
There are two types of these layers: Row LSTM layers apply the convolution along each row of pixels; Diagonal BiLSTM layers apply the convolution along the diagonals of the image (like a bishop moving on a chessboard).
Here’s an illustration of the Row LSTM convolution with a kernel size of 3 (3 pixels wide). Notice how it fails to reach pixels on the far sides of the image in rows close to .
![]()
In contrast, the Diagonal BiLSTM’s dependency field covers the entire available context in the image:
![]()
A Pixel CNN network is fully convolution and has up to fifteen layers, “We observe that CNNs can also be used as a sequence model with a fixed dependency range, by using Masked convolutions.”
With Masked Convolution the R,G,B channels for the current pixel are predicted separately. When predicting the R channel, only the pixels left and above can be used for conditioning. But when we predict the G channel, we can also use the predicted value for R at the current pixel. And when we predict the B value, we can use the predicted values for both R and G.
To restrict connections in the network to these dependencies, we apply a mask to the input-to-state convolutions and to other purely convolutional layers in a PixelRNN. We use two types of masks that we indicate with mask A and mask B, as shown [below]. Mask A is applied only to the first convolutional layer in a PixelRNN and restricts the connections to those neighboring pixels and to those colors in the current pixels that have already been predicted. On the other hand, mask B is applied to all the subsequent input-to-state convolutional transitions and relaxes the restrictions of mask A by also allowing the connection from a color to itself.
![]()
The Pixel CNN is the fastest architecture, whereas Pixel RNNs with Diagonal BiLSTM layers perform the best in terms of generating likely images. For generation of larger images, Multiscale Pixel RNNs do even better.
The Multi-Scale PixelRNN is composed of an unconditional PixelRNN and one or more conditional PixelRNNs. The unconditional network first generates a smaller s × s image just like a standard PixelRNN described above, where s is a smaller integer that divides n. The conditional network then takes the s × s image as an additional input and generates a larger n × n image.
![]()
One fun experiment that shows the power of the method is to occlude the lower part of an image, and then ask a PixelRNN to complete the image. Here are some example generated completions (with the original in the right-hand column for comparison):
![]()
Based on the samples and completions drawn from the models we can conclude that the PixelRNNs are able to model both spatially local and long-range correlations and are able to produce images that are sharp and coherent. Given that these models improve as we make them larger and that there is
practically unlimited data available to train on, more computation and larger models are likely to further improve the results.
Auto-encoding variational Bayes
The auto-encoding paper is short and dense, and I don’t feel able to add much value to it, so here’s a very short summary of what to expect if you go on to read it. The opening sentence sets the tone:
How can we perform efficient approximate inference and learning with directed probabilistic models whose continuous latent variables and/or parameters have intractable posterior distributions? [Oh, and we want to do it with large datasets].
I bet you were wondering exactly that in the shower this morning! Let’s unpack this sentence to see what it’s all about:
- ‘efficient approximate inference and learning’ simply says that we want a training approach which is not too costly to compute.
- ‘directed probabilistic models‘ are graph models where the probability at some node is conditioned on the probabilities of other nodes, with directed edges in the graph from cause nodes to affected nodes.
- ‘continuous latent variables‘ suggests that there are true hidden causes for the observed behaviour, which are not directly represented in our model (latent). These are real-valued (i.e., not discrete).
- ‘intractable posterior distributions‘ means that we can’t calculate an exact answer for the output probability distribution, so we’ll need to approximate it.
- The use of large datasets further stresses the need for efficiency.
The authors demonstrate a simple and efficient differentiable (i.e., easily trainable) estimator that fits the bill, which they call Stochastic Gradient Variational Bayes (SGVB). Using this in an autoencoder leads to Auto-Encoding Variational Bayes (AEVB).
If you’re feeling brave and want to dig in (or your knowledge of variational Bayesian methods is better than mine!), then these wikipedia entries on Variational Bayesian methods and Kullback-Leibler divergence might come in handy.