Strategic attentive writer for learning macro-actions Vezhnevets et al. (Google DeepMind), NIPS 2016

Baldrick may have a cunning plan, but most Deep Q Networks (DQNs) just react to what’s immediately in front of them and what has come before. That is, at any given time step they propose the best action to take there and then. This means they can perform very well on (for example) learning to play the Atari game Breakout, but they don’t do so well on games that require longer range planning. One of the games that caused particular trouble was Frostbite. So much so in fact, that the authors of “Building Machines that Learn and Think like Humans” dedicate a whole discussion to “the Frostbite challenge” (§3.2).

In this paper, Vezhnevets et al. propose a new deep recurrent neural network architecture they call a “STRategic Attentive Writer” (STRAW) that can make (Strawman?) plans for carrying out a sequence of actions over time.

Unlike the vast majority of reinforcement learning approaches which output a single action after each observation, STRAW maintains a multi-step action plan.

More specifically, STRAW learns ‘macro-actions‘ – common action sequences – based on rewards. STRAW also learns when to stick with the plan it has, and when it’s time to make a new plan.

Our proposed architecture is a step towards more natural decision making, wherein one observation can generate a whole sequence of outputs if it is informative enough.

And how well does STRAW do on the Frostbite challenge? It obtained a score of 8108, compared to the baseline score of 1281. The following figure shows examples of the action-sequences learned by STRAW(e) – these correspond to natural actions in the game such as jumping from floe to floe and picking up fish.

Let’s take a look at the STRAW architecture and how to train it, before diving into some more results.

Model architecture

STRAW consists of two modules working in concert. The action module is responsible for translating input from the environment into an action plan. The commitment module decides how long to stick with the current action plan vs abandoning it and forming a new plan.

The action plan at time is represented by a matrix where is the total number of possible actions and is the maximum time horizon of a plan. An entry in the matrix represents the probability of outputting the given action at the given timestep.

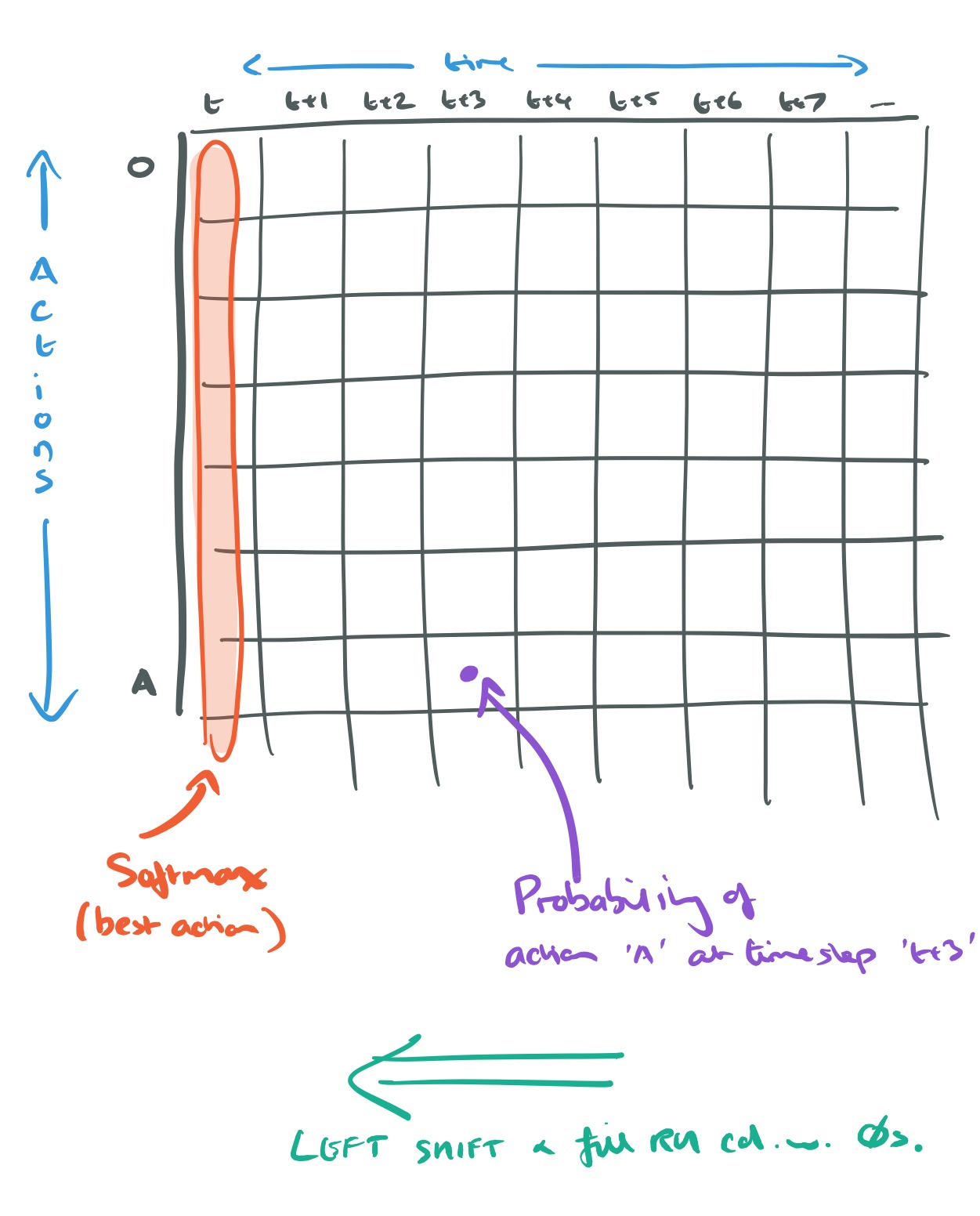
To generate the next action (at time ), the first column of the matrix is transformed into a distribution over possible actions using softmax. While following a plan, after outputting the action for time t the action matrix is shifted by removing the first column and appending a column filled with zeros as the new right-most column.

The commitment plan is represented by a single row matrix (transposed vector) . A binary random variable is sampled from . If is 0 then plans are committed to at this time step. If is 1 then re-planning occurs.

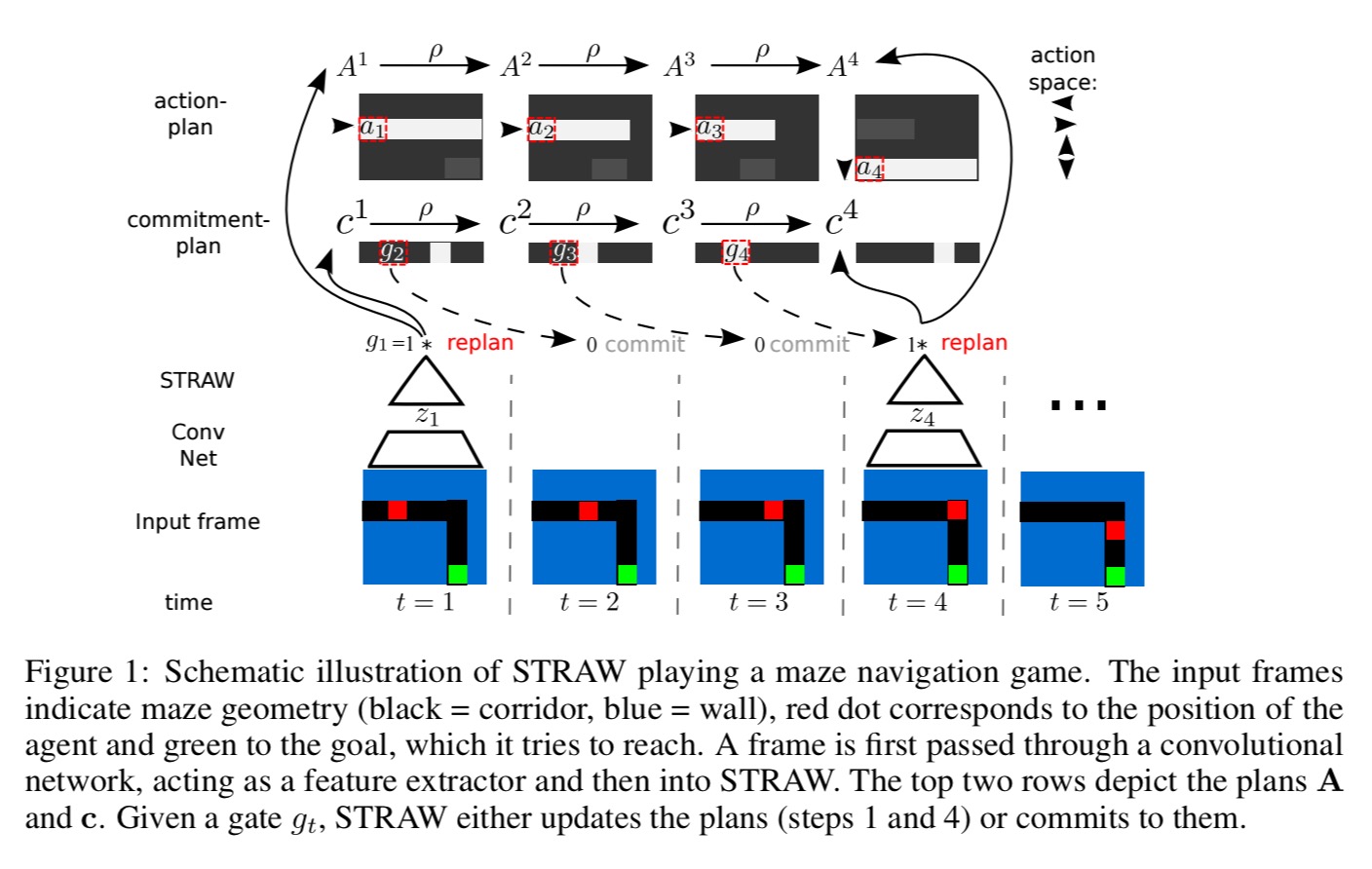
The complexity of the (action plan) sequence and its length can vary dramatically even within one environment. Therefore the network has to focus on the part of the plan where the current observation is information of desired actions. To achieve this, we apply differentiable attentive reading and writing operations, where attention is defined over the temporal dimension.

(The network is given a memory, indexed by plan time).

If is a feature representation of an observation , then STRAW computes an update to the action plan using the algorithm shown below. and are linear functions and is a two-layer perceptron.

The commitment plan is updated at the same time as the action plan if = 1. After 40 time steps (in the experiments) a re-plan is guaranteed to happen.

STRAWe (as used for the Frostbite challenge) is a version of STRAW with a noisy communication channel between the feature extractor and the STRAW planning modules. This noise generates randomness encouraging exploration of plan steps.

Training

Training follows the standard reinforcement learning approach where an agent interacts with an environment is discrete time, selecting an action at each time step and being given a new state and a scalar reward. The goal of the agent is to maximize its discounted return. Training uses the Asynchronous Actor-Critic (A3C) method that we looked at last year.

Results

The team explored three different scenarios: supervised next character prediction in text, a 2D maze game, and a selection of ATARI games.

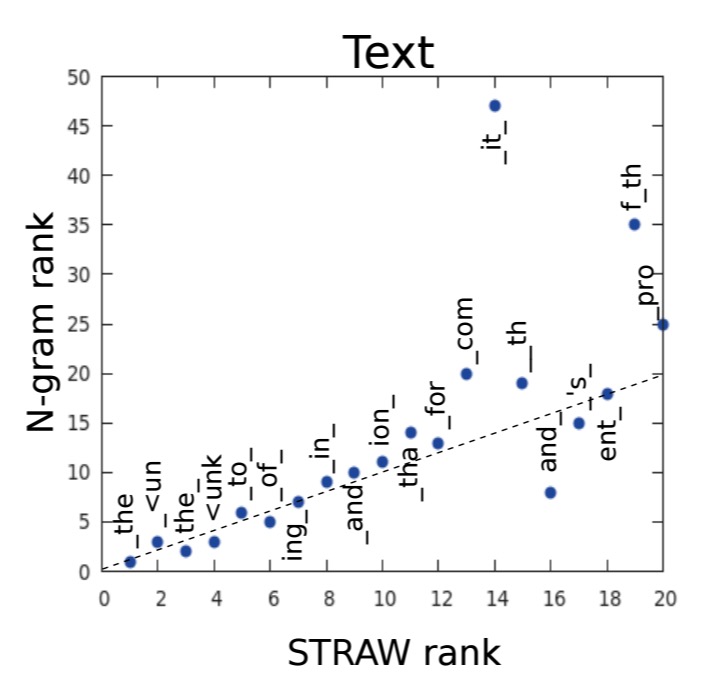
The text prediction example shows the ability of STRAW to learn useful sequences – actions correspond to emitting characters and macro-actions to sequences of characters.

If STRAW adequately learns the structure of the data, then its macro-actions should correspond to common m-grams…

And indeed they do:

In the 2D maze environment a STRAWe agent is trained on an 11×11 random maze environment and then tested in a novel maze using varying start and goal locations. In the visualisation below, the red intensity indicates how often the agent re-planned at a given location normalized by number of visits.

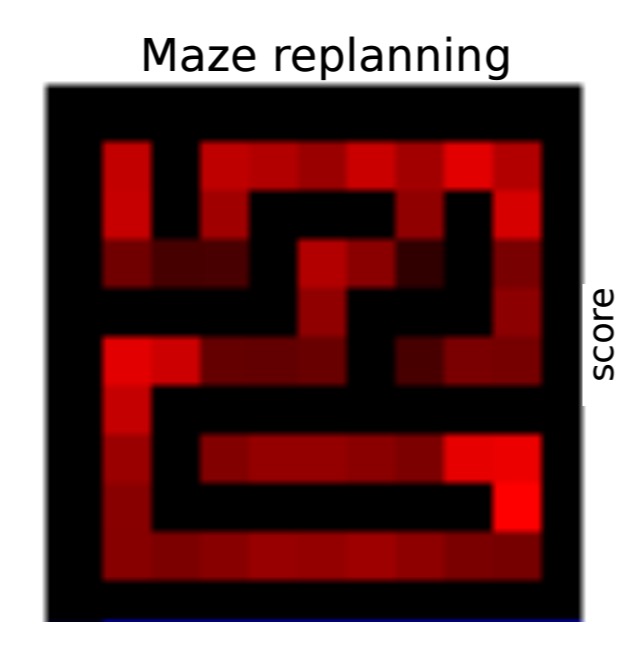
Notice how corners and areas close to junctions are highlighted. This demonstrates that STRAW learns adequate temporal abstractions in this domain.

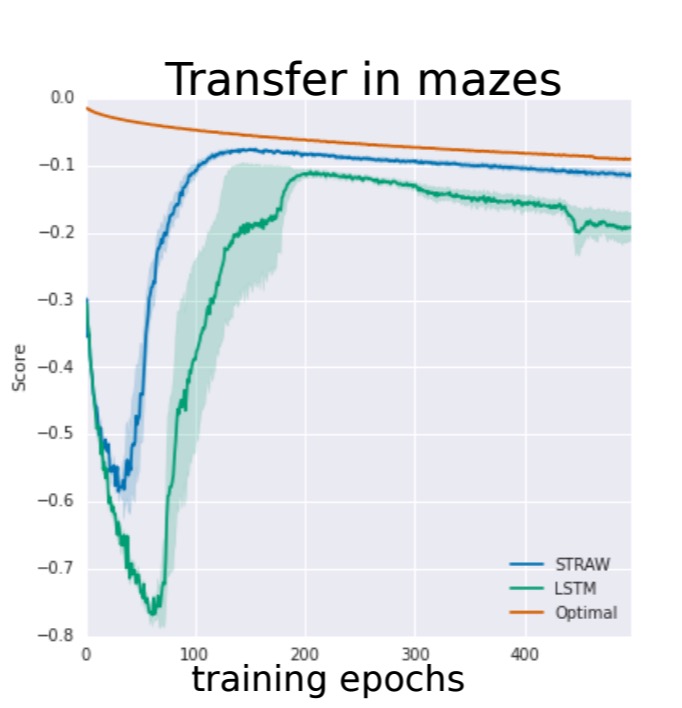
Shifting to a 15×15 maze, STRAW is compared to an LSTM baseline and the optimal path given by the Dijkstra algorithm. As training epochs (2 million training steps) progress, the goal is move progressively further away from the start point. LSTM starts to show a strong drop-off compared to optimal policy, but STRAWe continues to perform well.

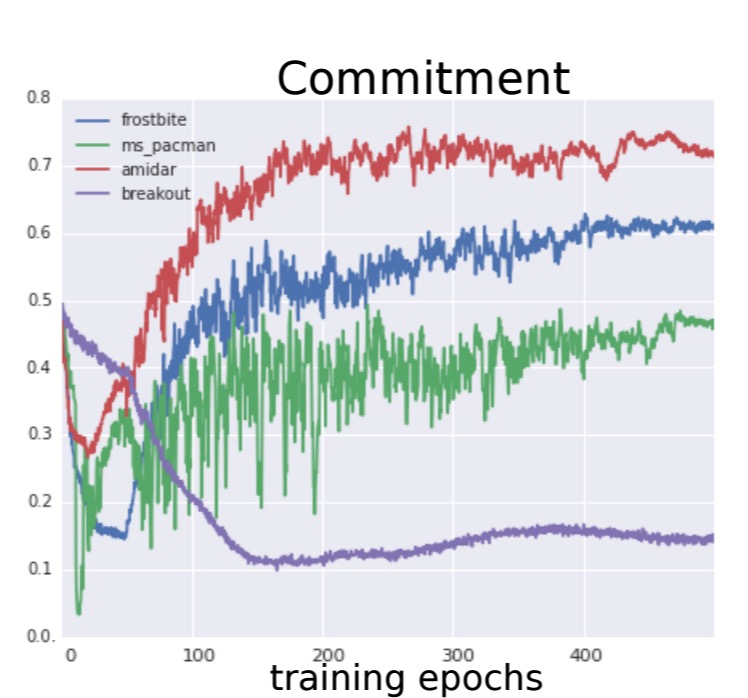
On a selection of ATARI games, STRAWe learns to commit more to action sequences as training progresses, and converges to a stable regime after about 200 epochs.

We previously saw how well STRAWe did on Frostbite. Here’s a look at STRAWe’s learned plans on the Amidar game:

… STRAW advances the state-of-the-art on several challenging Atari domains that require temporally extended planning and exploration strategies, and also has the ability to learn temporal abstractions in general sequence prediction. As such it opens a fruitful new direction in tackling an important problem area for sequential decision making and AI more broadly.