Learning to prove theorems via interacting with proof assistants Yang & Deng, ICML’19

Something a little different to end the week: deep learning meets theorem proving! It’s been a while since we gave formal methods some love on The Morning Paper, and this paper piqued my interest.

You’ve probably heard of Coq, a proof management system backed by about 30 years of research and developed out of INRIA. Here’s how the Coq home page introduces it:

Coq is a formal proof management system. It provides a formal language to write mathematical definitions, executable algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs.

Certified programs can then be extracted to languages like OCaml, Haskell, and Scheme.

In fully automated theorem proving (ATP), after providing a suitable formalism and a theorem, the goal is to be able to push a button and have the system prove that the theorem is true (or false!). The state-of-the-art in ATP is still some way behind human experts though it two key areas: the scale of systems it can tackle, and the interpretability of the generated proofs.

What a typical theorem prover does… is to prove by resolution refutation: it converts the premises and the negation of the theorem into first-order clauses in conjunctive normal form. It then keeps generating new clauses by applying the resolution rule until an empty clause emerges, yielding a proof consisting of a long sequence of CNFs and resolutions.

Enter interactive theorem proving (ITP). In ITP a human expert guides the structure of the proof, telling the system which proof tactics to use at each step:

The tactics capture high-level proof techniques such as induction, leaving low-level details to the software referred to as proof assistants.

(Enlarge)

It would be nice if we could learn from all the ITP proofs that humans have generated, and use those learnings to improve the proof steps that a system can take automatically:

… human experts have written a large amount of ITP code, which provides an opportunity to develop machine learning systems to imitate humans for interacting with the proof assistant.

Such a combination would get us closer to fully automated human-like proofs.

To pull all this together we need three things:

1. A large ITP dataset we can learn from
2. A learning environment for training and evaluating auto-ITP agents. Agents start with a set of premises and a theorem to prove, and then they interact with the proof assistant by issuing a sequence of tactics.
3. A way to learn and generate new tactics which can be used in the construction of those proofs.

The first two requirements are satisfied by CoqGym, and ASTactic handles tactic generation.

CoqGym

CoqGym (https://github.com/princeton-vl/CoqGym) includes a dataset of 71K human-written proofs gathered from 123 open-source Coq projects. Every proof is represented as a tree with goals (and their context) as nodes, and tactics as edges between nodes. On average proofs in the dataset have 8.7 intermediate goals and 9.1 steps. The projects are split into training, test, and validation sets resulting in 44K training proofs, 14K validation proofs, and 13K testing proofs.

In addition to the human-generated proofs, CoqGym also includes shorter proofs extracted from the intermediate goals inside long proofs. For every intermediate goal in a human-written proof, synthetic proofs of 1, 2, 3, and 4 steps are generated.

Learning to theorem prove in Coq resembles a task-oriented dialog with an agent receiving current goals, local context, and global environment at each step, and issuing a tactic for the system to use. Agents can be trained using supervised or reinforcement learning.

ASTactic

ASTactic is a deep learning model for tactic generation that generations tactics as programs by composing ASTs in a predefined grammar using a subset of Coq’s tactic language.

Compared to prior work that chooses tactics from a fixed set, we generate tactics dynamically in the form of abstract syntax trees and synthesize arguments using the available premises during runtime. At test time, we sample multiple tactics from the model. They are treated as possible actions to take, and we search for a complete proof via depth-first search (DFS).

ASTatic is built using an encoder-decoder architecture. The encoder embeds a proof goal and premises expressed in ASTs, and the decoder generates a program-structured tactic by sequentially growing an AST.

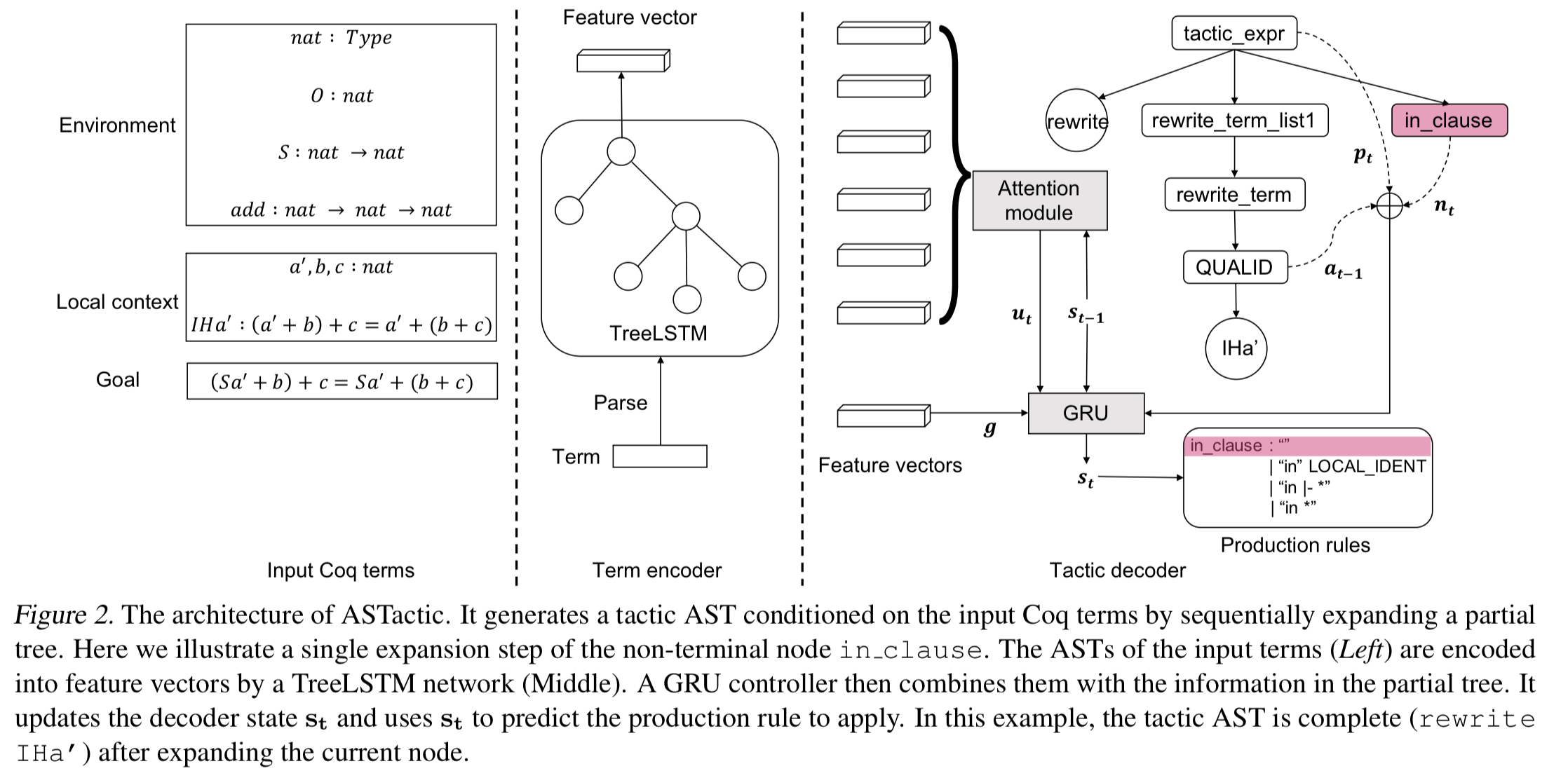
(Enlarge)

The production rule to apply is selected using a softmax over rule outputs. The argument(s) for the rule are then selected according to their type:

• For rules that take a premise argument (e.g., H in apply H) a score is computed for each premise in either the environment or the local context, and then a premise is selected using a softmax over these scores.
• For rules with an integer argument, most take an argument between 1 and 4, so a 4-way classifier is used to select one.
• For quantified variables in the goal, a universally quantified variable in the goal is selected at random.

Can you prove it?

We evaluate ASTactic on the task of fully-automated theorem proving in Coq, using the 13,137 testing theorems in CoqGym. The agent perceives the current goals, their local context, and the environment. It interacts with Coq by executing commands, which include tactics, backtracking to the previous step (Undo), and any other valid Coq command. The goal for the agent is to find a complete proof using at most 300 tactics and within a wall time of 10 minutes.

Performance is compared against Coq’s built-in automated tactics (trivial, auto, intuition, and easy), and against hammer. Hammer simultaneously invokes Z3, CVC4, Vampire, and EProver and returns a proof if any one of them succeeds. It sets a time limit of 20 seconds for all these external systems.

The automated tactics can also be combined with ASTactic, whereby at each step the agent first using an automatic tactic to see if it can solve the current goal. If it can’t be solved automatically, the agent executes a tactic from ASTactic to decompose the goal into sub-goals.

In the best performing combination (ASTactic + hammer), 30% of theorems in the test set can be proved.

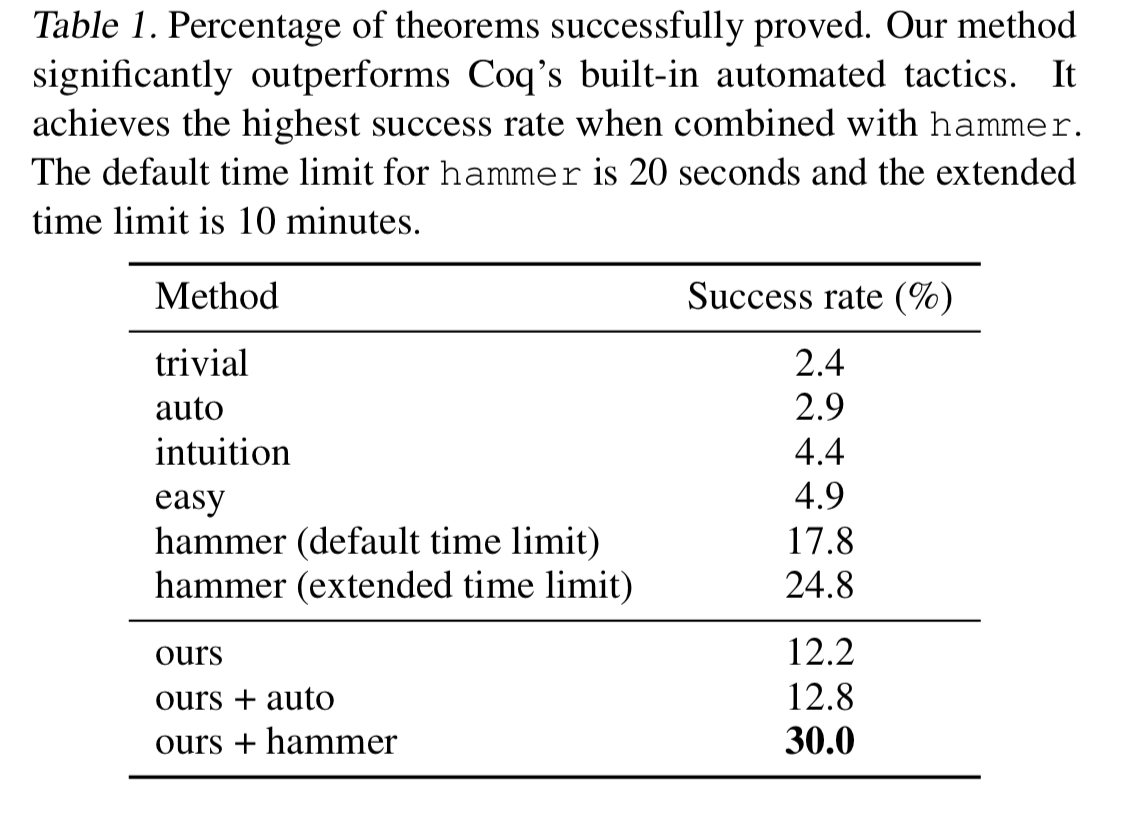
This demonstrates that our system can generate effective tactics and can be used to prove theorems previously not provable by automatic methods.

As an extra bonus, the generated proofs tend to be shorter than the ground truth proofs collected in CoqGym:

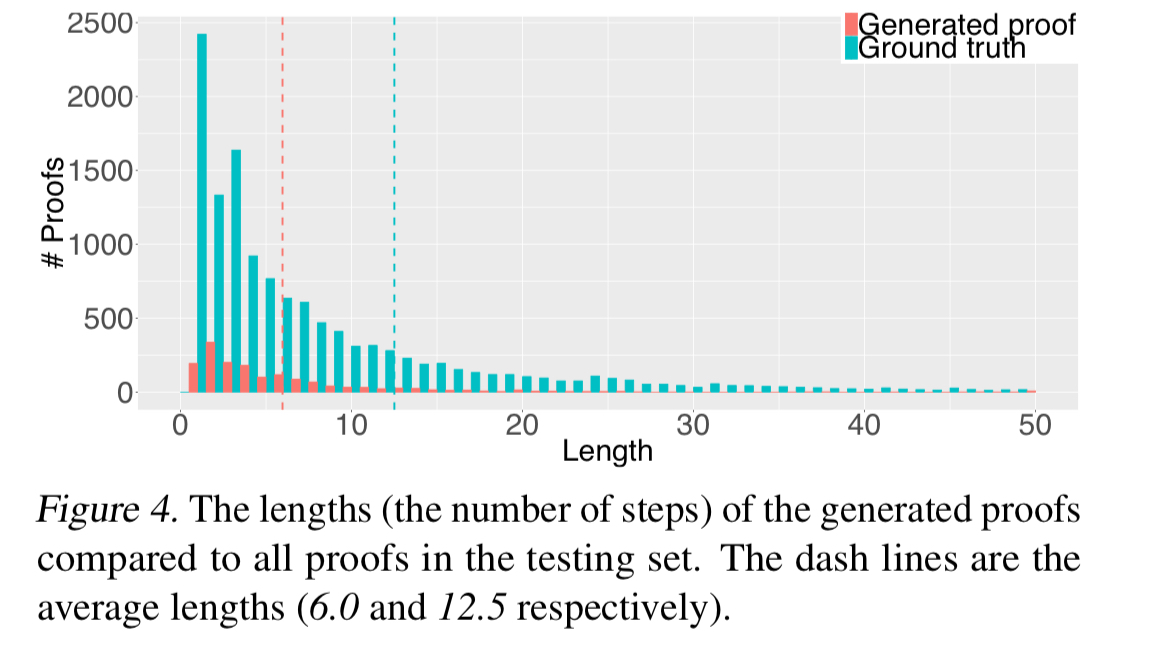
Presumably you could take this system and use it as an even more powerful ITP, with human guidance still being provided where it struggles. After enough time, we could then learn from the human-assisted proofs that were generated, and go round the loop all over again!

If you liked this, you might also enjoy “The great theorem prover showdown.”