PyTorch-BigGraph: a large-scale graph embedding system

~ Adrian Colyer

PyTorch-BigGraph: a large-scale graph embedding system Lerer et al., SysML’19

We looked at graph neural networks earlier this year, which operate directly over a graph structure. Via graph autoencoders or other means, another approach is to learn embeddings for the nodes in the graph, and then use these embeddings as inputs into a (regular) neural network:

Working with graph data directly is difficult, so a common technique is to use graph embedding methods to create vector representations for each node so that distances between these vectors predict the occurrence of edges in the graph.

When you’re Facebook, the challenge in learning embeddings is that the graph is big: over two billion user nodes, and over a trillion edges. Alibaba’s graph has more than one billion users and two billion items; Pinterest’s graph has more than 2 billion entities and over 17 billion edges. At this scale we have to find a way to divide-and-conquer. We’ll need to find some parallelism to embed graphs with trillions of edges in reasonable time, and a way of partitioning the problem so that we don’t need all of the embeddings in memory at each node (‘many standard methods exceed the memory capacity of typical commodity servers’).

Facebook’s answer to this problem is PyTorch-BigGraph (PBG). PBG can scale to graphs with billions of nodes and trillions of edges. At the core of PBG is a partitioning scheme based on a block decomposition of the adjacency matrix. Once the graph is partitioned a distributed execution model becomes possible to speed up training.

In addition to internal use at Facebook, PBG has been used to construct an embedding of the full Freebase knowledge graph (121M entities, 2.4B edges). Using 8 machines decreased training time by a factor of 4, and memory consumption was reduced by 88%. The embeddings have been made publicly available as part of this work.

The embedding model

PBG works with multi-relation graphs, i.e., there are multiple entity types and multiple possible relation types (edge types). We want to learn a vector representation \theta for each entity type and each relation type. Edges are represented by (source, relation, destination) tuples (s, r, d) .

A multi-relation graph embedding uses a score function f(\theta_{s}, \theta_{r}, \theta_{d}) that produces a score for each edge that attempts to maximize the score of f(\theta_{s}, \theta_{r}, \theta_{d}) for any (s, r, d) \in E and minimizes it for (s, r, d) \notin E .

In PBG each relationship type can be associated with a relation operator g which can be e.g. linear transformation, translation, or complex multiplication. g is used to transform a (node, relation) pair representation either the source or destination of an edge. The score f is then computed based on the similarity of the transformed source and destination nodes connected by an edge. PBG uses either dot product or cosine similarity.
\displaystyle f(\theta_{s}, \theta_{r}, \theta_{d}) = sim (g_{(s)}(\theta_{s},\theta_{r}), g_{(d)}(\theta_{d},\theta_{r}))
By choosing appropriate similarity and relation operators a number of common models from the literature (e.g. RESCAL, DistMult, TransE, ComplEx) can be trained.

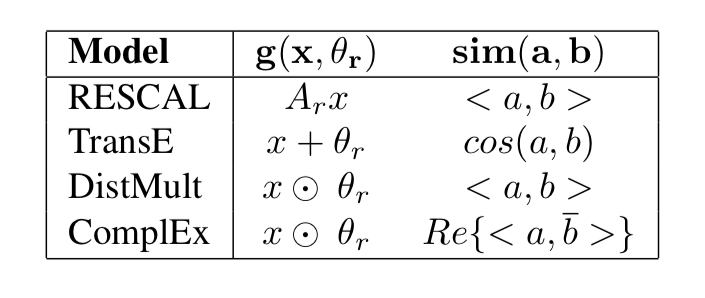
PBG works with sparse graphs, so the input is a list of edges. These are the positive examples used for training. We’re also going to need a set of negative examples (edges that don’t exist in the graph). These are constructed through sampling by first selecting an existing positive edge, and then changing either the source of destination node. The way in which we sample nodes can impact the outcome, especially with highly-skewed graphs.

On one hand, if we sample negatives strictly according to the data distribution, there is no penalty for the model predicting high scores for edges with rare nodes. On the other hand, if we sample negatives uniformly, the model can perform very well (especially in large graphs) by simply scoring edges proportional to their source and destination node frequency in the dataset.

PBG combines both kinds of sampling to reduce these undesirable effects, by default sampling 50% of the time uniformly at random, and 50% of the time based on node prevalence in the training data.

Partitioning nodes and edges

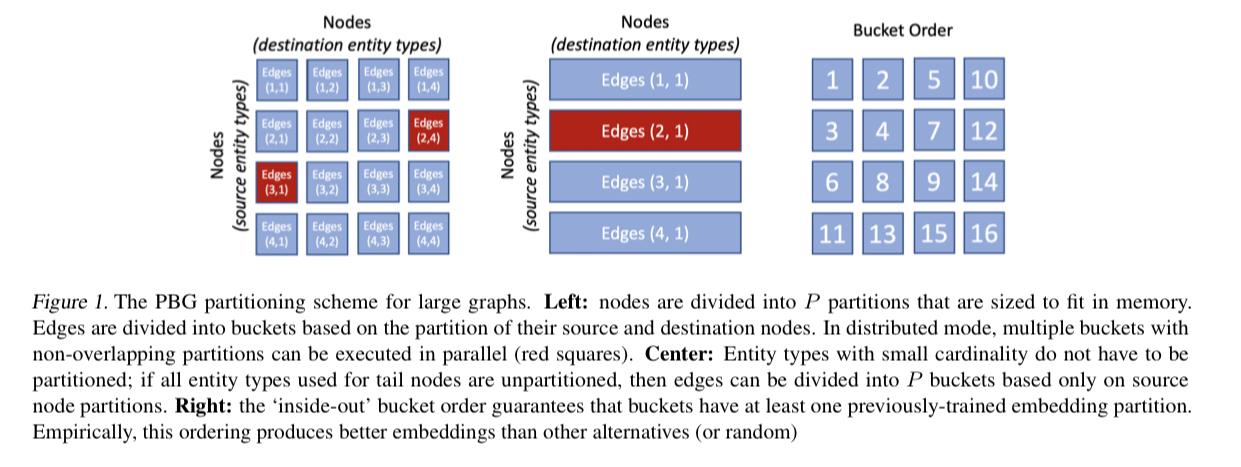
Each entity type in the graph can be individually partitioned (or left unpartitioned). A partitioned entity is split into P parts to ensure that each part fits into memory and that the desired level of parallelism in training is supported.

Given an entity partitioning, we need to construct an edge partitioning (recall that we train over (source, relation, destination) triples). Edges are divided into buckets based on the partitions of their source and destination entities. If an edge has a source in partition p_1 and a destination in partition p_2 then it will be placed in bucket (p_1, p_2) . Thus we have up to P^2 buckets.

Each epoch of training iterates though the edge buckets. Compared to the base algorithm this means that edges are now grouped by partition when sampling, and negative edge examples are drawn from the bucket partitions.

The order in which we iterate over the edge buckets matters. After the very first bucket (p_1, p_2), we need to ensure that in every subsequent iteration one of the source or destination buckets has previously been trained. E.g., for the second iteration valid options are (p_1, *) or (*, p_2) .

This constraint ensures that embeddings in all partitions are aligned in the same space. For single-machine embeddings, we found that an ‘inside-out‘ ordering, illustrated in Figure 1, achieved the best performance while minimizing the number of swaps to disk.

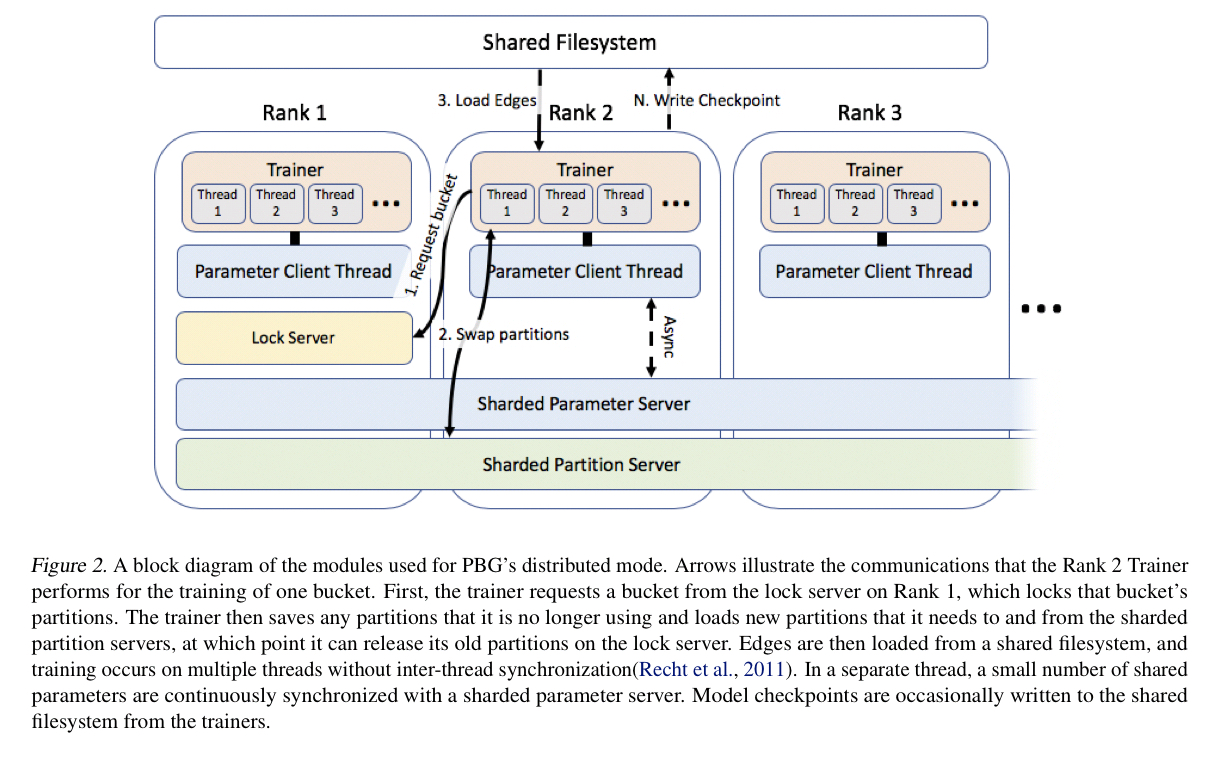
Distributed execution

For distributed execution PBG uses a locking scheme over partitions combined with an asynchronous parameter server architecture for shared parameters (relation parameters and entity types using featurized embeddings, but overall a small number compared to the total). The lock server respects the bucket ordering constraint for iteration, and favours re-using partitions at workers when assigning buckets so as to minimise communication overheads.

Efficient negative sampling for large graphs

Making negative samples turns out to be a big contributor to memory consumption and training times.

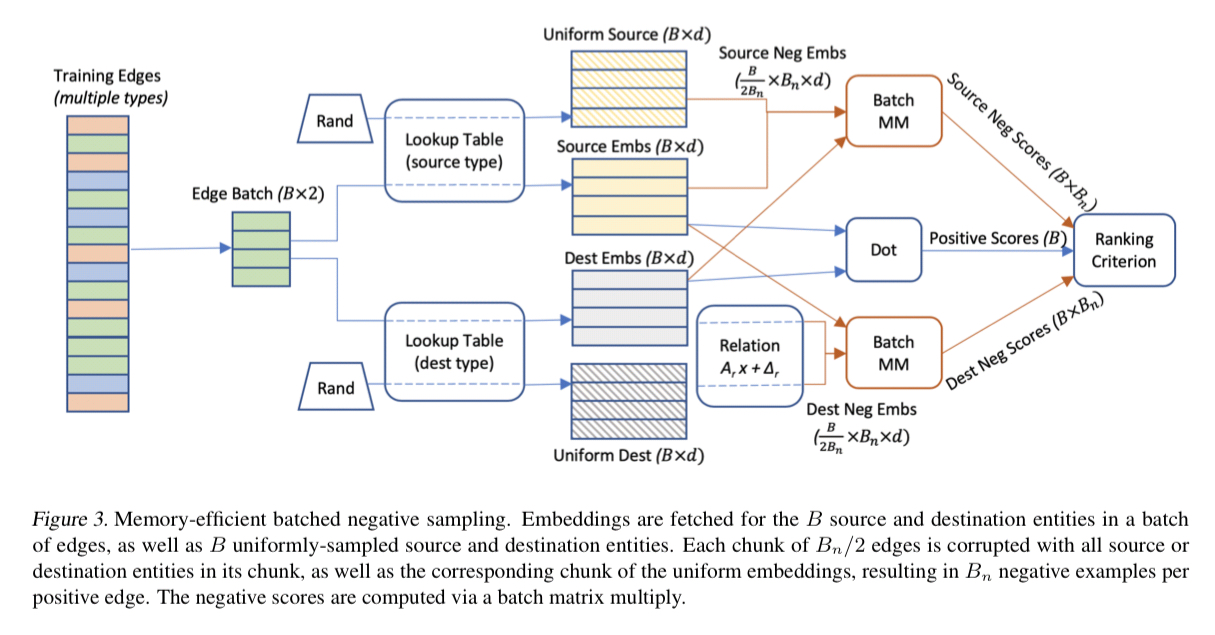
To increase memory efficiency on large graphs, we observe that a single batch of B_n sampled source or destination nodes can be reused to construct multiple negative examples.

PBG is typically configured to take a batch of B=1000 positive edges. These are broken in 20 chunks of 50 edges each. The destination (source) embedding from each chunk is concatenated with 50 embeddings sampled uniformly from the source (destination) entity type. For each batch of B positive edges only 3B embeddings are fetched from memory and 3BB_n edge scores (dot products) are computed. The edge scores for a batch can be computed via an efficient batched B_n \times B_n matrix multiplication.

Evaluation

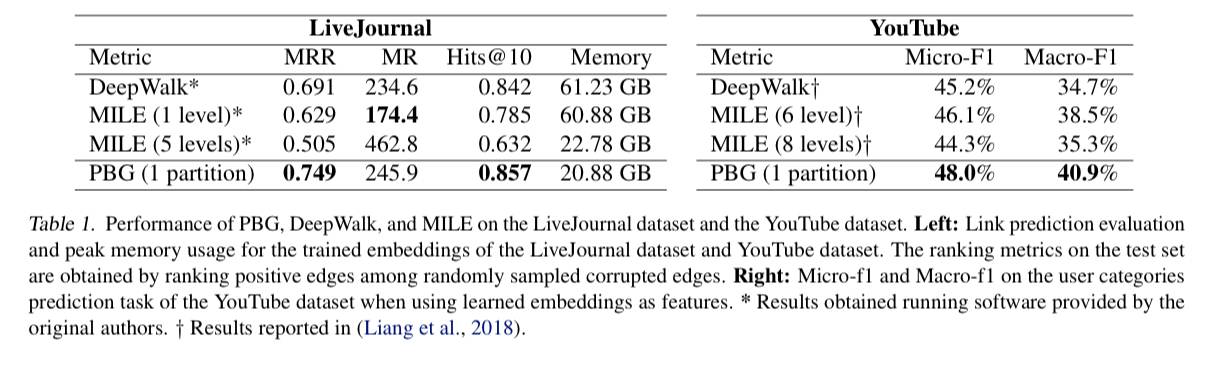
PBG is evaluated using a variety of online social network graphs (LiveJournal, Twitter, YouTube) as well as the Freebase knowledge graph.

We find that PBG is much faster and more scalable than existing methods while achieving comparable performance. Second, the distributed partitioning does not impact the quality of the learned embeddings on large graphs. Third, PBG allows for parallel execution and thus can decrease wallclock training time proportional to the number of partitions.

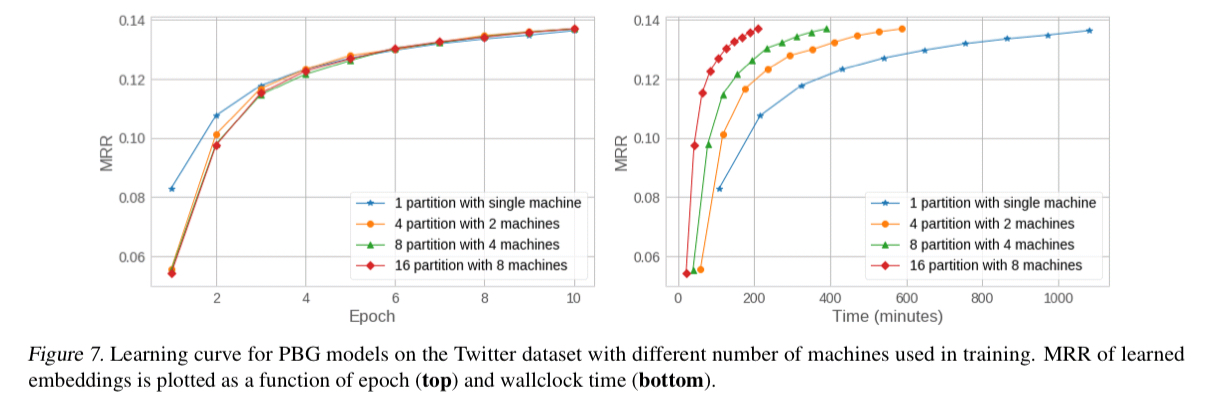
When training using the Freebase knowledge graph, ComplEx models with multiple partitions and machines were unstable, and getting to the bottom of why this is so is future work.

PBG is available on GitHub if you want to experiment with it.