Learning the structure of generative models without labeled data

~ Adrian Colyer

Learning the structure of generative models without labeled data Bach et al., ICML’17

For the last couple of posts we’ve been looking at Snorkel and BabbleLabble which both depend on data programming – the ability to intelligently combine the outputs of a set of labelling functions. The core of data programming is developed in two papers, ‘Data programming: creating large training sets, quickly’ (Ratner 2016) and today’s paper choice, ‘Learning the structure of generative models without labeled data’ (Bach 2017).

The original data programming paper works explicitly with input pairs (x,y) (e.g. the chemical and disease word pairs we saw from the disease task in Snorkel) which (for me at least) confuses the presentation a little compared to the latter ICML paper which just assumes inputs x (which could of course have pair structure, but we don’t care about that at this level of detail). Also in the original paper dependencies between labelling functions are explicitly specified by end users (as one of four types: similar, fixing, reinforcing, and exclusive) and built into a factor graph. In the ICML paper dependencies are learned. So I’m going to work mostly from ‘Learning the structure of generative models without labeled data’ in this post, and concentrate just on the core development of the theory.

A generative probabilistic model for accuracy estimation under independence

We have input data points x_{i}, and for each x_{i} a latent variable y \in \{-1, 1\} that is its true label. We don’t know y_{i}, but we do have n labelling functions \lambda_{1}, ..., \lambda_{n}.

Each labelling functions takes as input an data point x_i and produces as output a value \Lambda which is either true, abstain, or false ( \{1, 0, -1\} ). (The approach generalises to the multi-class case).

We start out by assuming that the outputs of the labelling functions are conditionally independent given the true label. Consider a labelling function \lambda_{j}, which gives output \Lambda_{ij} on input x_{i} (with true label y_i). We can model the accuracy of this labelling function with \phi_{j}^{Acc}. We’ll say the accuracy function has value 1 if \lambda_{j} correctly labels an example, and 0 otherwise. In our setting this can be succinctly expressed as:

\displaystyle \phi_{j}^{Acc}(\Lambda_i, y_i) = y_i \Lambda_{ij}

The accuracy function itself is controlled by some parameter \theta_{j}^{Acc} modelling how accurate each labelling function is.

Now for m input examples and n labelling functions, we have a conditionally independent model

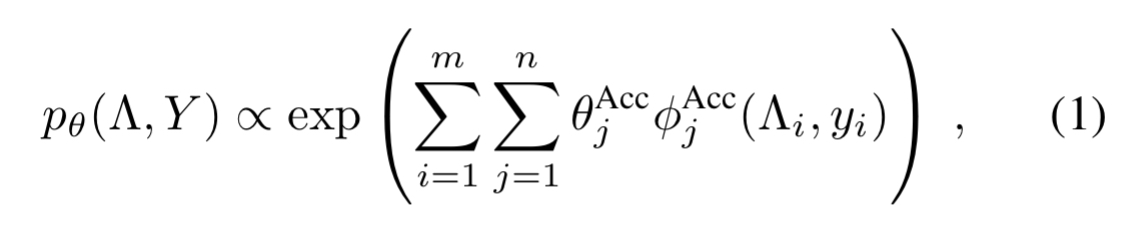
where Y is the set of true labels y_1, ..., y_m.

The unknown parameters \theta modelling the accuracy of the labelling functions can now be estimated by minimising the negative log marginal likelihood of failing to give the correct label (guessing a wrong label, or abstaining).

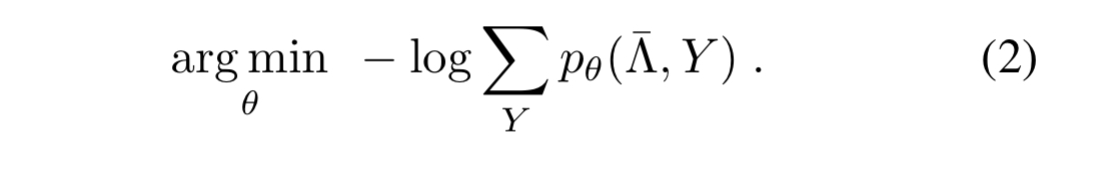
We can do this using standard stochastic gradient descent, where the gradient for parameter \theta_{j}^{Acc} is given by the number of examples \lambda_j correctly labels minus the number of examples it fails to label correctly.

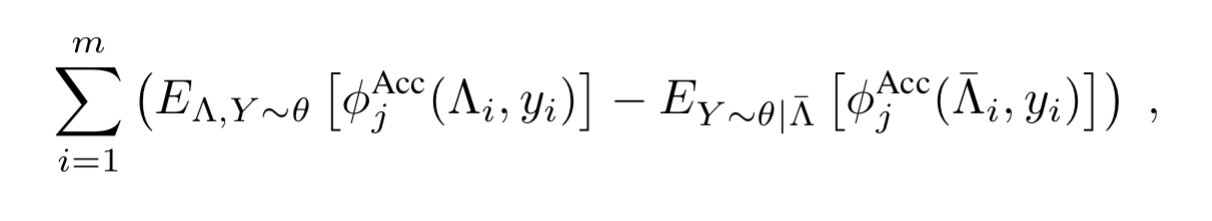
Structure learning

The conditionally independent model is a common assumption, and using a more sophisticated generative model currently requires users to specify its structure.

As we know from the Snorkel paper, unfortunately labelling functions are often not independent.

To address this issue, we generalize the conditionally independent model as a factor graph with additional dependencies, including higher-order factors that connect multiple labeling function outputs for each data point x_i and label y_i.

Suppose there is a set T of dependency types of interest, where a dependency type represents a form of dependency between labelling functions, such as correlation. Unknown to us, there is also a set S_t of index tuples which indicate the set of labelling functions that participate in each dependency of type t \in T. This gives us a general model of the form

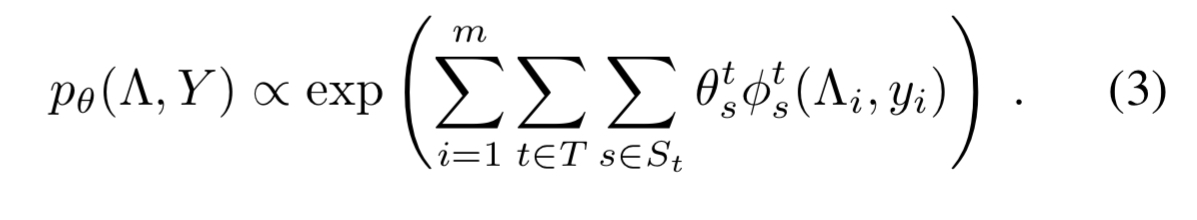
and we want to learn the parameters \theta_{s}^{t}.

Estimating the structure of the distribution p_{\theta}(\Lambda, Y) is challenging because Y is latent; we never observe its value, even during training. We must therefore work with the marginal likelihood p_{\theta}(\Lambda). Learning the parameters of the generative model requires Gibbs sampling to estimate gradients. As the number of possible dependencies increases at least quadratically in the number of labeling functions, this heavyweight approach to learning does not scale.

The way out is to consider each labelling function in turn, optimising the log marginal pseudolikelihood of its outputs conditioned on the outputs of all the other labelling functions.

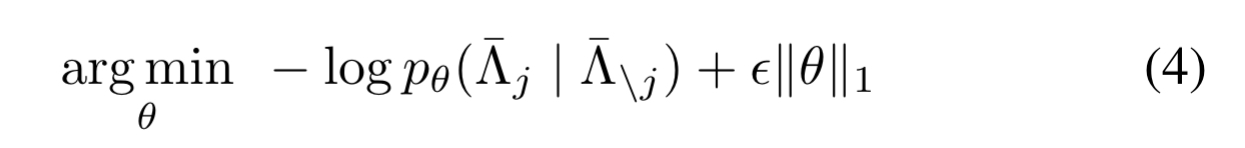
where \epsilon is a hyperparameter.

By conditioning on all other labeling functions in each term…, we ensue that the gradient can be computed in polynomial time with respect to the number of labeling functions, data points, and possible dependencies; without requiring any sampling or variational approximations.

It all comes together in the following algorithm:

The hyperparameter \epsilon controls the threshold and regularization strength and requires tuning. For the other parameters the authors fix these at step size = m^{-1}, epoch count = 10, and truncation frequency = 10.

Theoretical guarantees

Assuming that there exist some set of parameters which can capture the true dependencies within the model we are using, and that all non-zero parameters are bounded away from zero (have at least a minimum magnitude \kappa), then we can uncover the exact dependency structure with probability at least 1 - \delta given m inputs, where

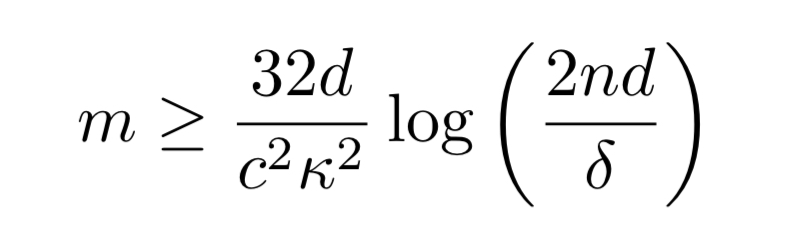
Where d is the maximum number of possible dependencies a single labelling function (or true label) can be involved in, and c is a measure of how much better our dependency estimates are with each labeling function than without (my loose interpretation of c – see eqn 7 in section 4 of the paper for the official definition).

If we further assume that the only dependency types are accuracy and correlation dependencies then we need an input dataset of size

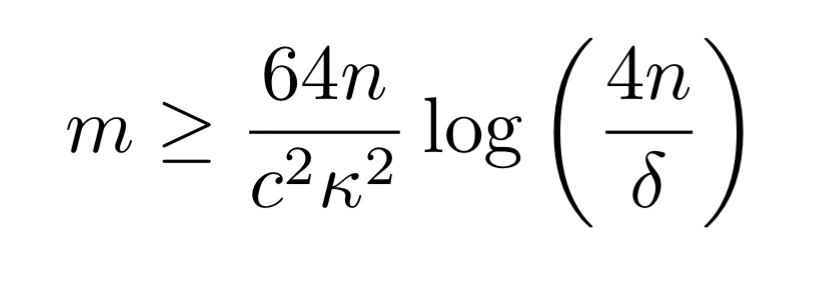
Practical results

Our analysis… guarantees that the sample complexity grows at worst on the order O(n \log n) for n labeling functions. In practice, we find that structure learning performs better than this guaranteed rate, depending linearly on the number of true correlations and logarithmically on the number of possible correlations.

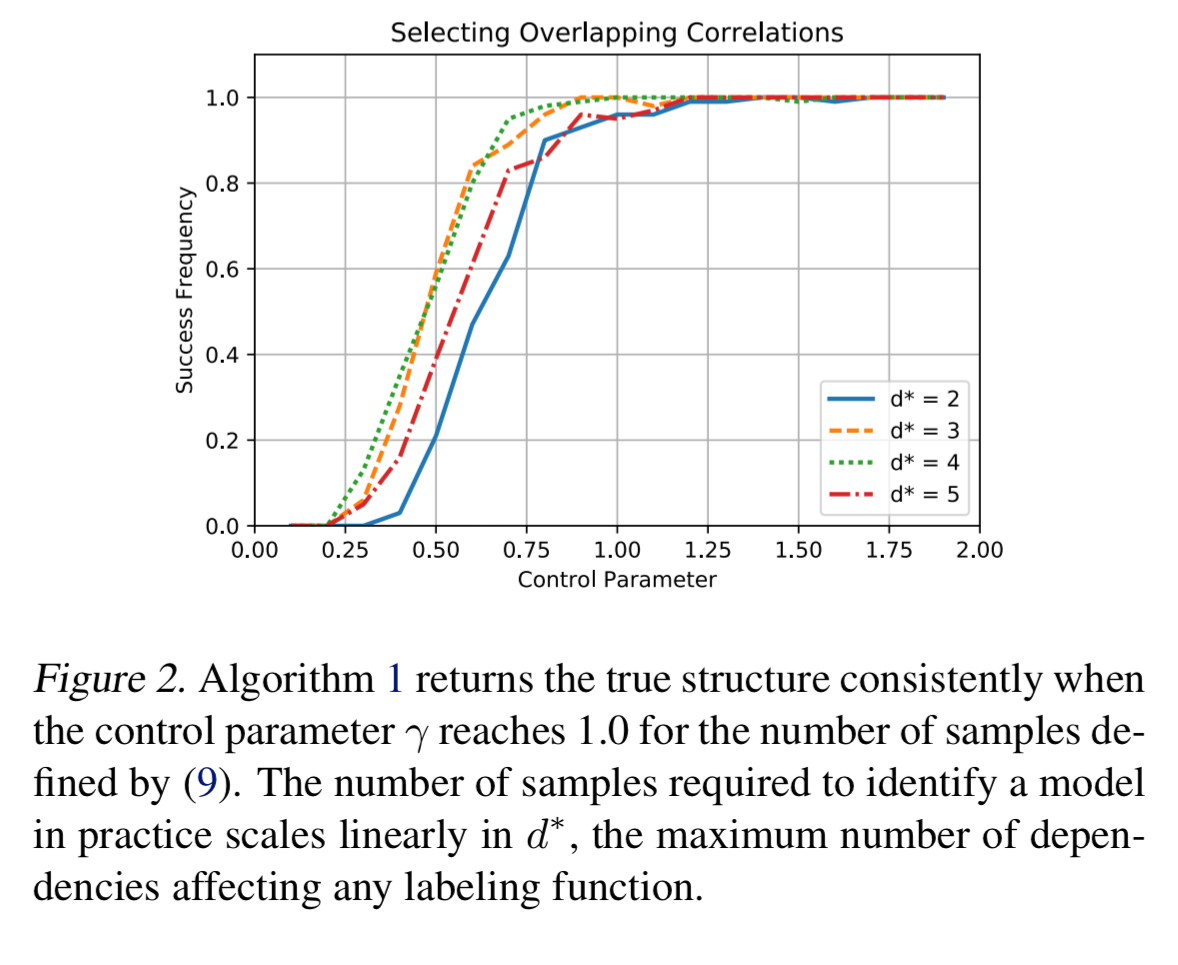
Compared to estimating structures via parameter learning over all possible dependencies, algorithm one is 100x faster and selects only 1/4 of the extraneous correlations.