Putting data in the driver’s seat: optimising earnings for on-demand ride hailing

~ Adrian Colyer

Putting data in the driver’s seat: optimising earnings for on-demand ride hailing Chaudhari et al., WSDM’18

(The link above is to the ACM Digital Library official version, which may not grant you access when clicked in your email client, but should do if you visit via the blog itself.)

There is something deeply rooted in the British psyche about routing for the underdog. I hope you enjoy this paper as much as I did!

The likes of Uber have plenty of technology at their disposal to optimise their businesses, but what about the individual drivers trying to make a living on their platforms? What strategy should a driver follow to maximise their earnings? Is it worth chasing surge pricing for example? Chaudhari et al. bring some computer science to the aid of the driver, showing optimal strategies that can increase a driver’s earnings by up to 50%!

Our first key takeaway is that a naive driver, armed with no data, and driving a 9-5 random walk schedule, is leaving roughly a 50% pay rise on the table by not driving more strategically. In contrast, a data-savvy driver armed with good historical data can build a forecast and optimal contingency driving plans with relatively little computational overhead using our dynamic programming algorithms, that have provable resilience to uncertainty.

(In the naive random walk schedule, a driver goes to locations dictated exclusively by the passengers picked up, and then waits in the current zone for the next passenger pick-up).

… the challenge of how to maximise one’s individual earnings as a driver for a ride-hailing platform like Uber or Lyft is a pressing question that millions of entrepreneurs across the world now face. Anecdotally, many drivers spend a great deal of time strategizing about where and when to drive. However, drivers today are self-taught, using heuristics of their own devising or learning from one another, and employ relatively simple dashboards such as SherpaShare.

The basic structure of the paper is as follows. First the authors set up a model of the problem space assuming that we have perfect information about journey times and rewards etc.., and then they show optimal driver strategies under that model. Then uncertainty is introduced, and we see that the strategies are robust to noise. Using a dataset combining NYC taxi rides with Uber API data for pricing, simulations of the various strategies are then performed, with some very illuminating findings. Let’s dive in!

Modelling the problem in a world of perfect information

Cities are divided into non-overlapping zones, and there are edges between zones. We need to know three basic things:

  1. If I’m in zone i, what’s the probability of picking up a passenger that wants to go to zone j? This information is captured in a transition matrix, F. The entry f(i,i) represents the probability of a driver not finding a passenger in zone i at a given time step.
  2. How long will it take me to travel from zone i to zone j? This information is captured in a travel time matrix, T.
  3. What is the driver’s net reward (earnings – costs) for taking a passenger from zone i to zone j? This information is captured in a rewards matrix, R.

Each of the above three matrices are time-dependent, i.e., their entries could change throughout the day.

Drivers have a home zone from which they start their shift, and to which they return at the end of a shift. Whenever a driver is faced with a decision, there are three basic actions they can take:

  • a_0 Get Passenger: wait for a passenger in the current zone
  • a_1 Go Home: log out of the ride service, relocate to the home zone if needed, and stop working
  • a_2(j) Relocate: relocate to city zone j (without taking a passenger).

Drivers have a maximum work budget of B time units.

A driver policy \pi is a sequence of time and location dependent actions taken by a driver at different steps of the strategy. (Aside: this would also be a really interesting setup for a reinforcement learning agent).

Given the above, we can calculate the expected earnings of a driver taking a given action at a given time.

Let E(i,t,a) be the expected earnings for taking action a at time t when in zone i. Then the total expected earnings for a driver following policy \pi is determined is:

\displaystyle \mathcal{E}(\pi, \mathbf{F},\mathbf{T},\mathbf{R},B) = \sum\limits_{(\hat{i}, \hat{t}, \hat{a}) \in \pi} E(\hat{i},\hat{t},\hat{a})

And finally we can state the Max Earnings problem: Given sets of time-evolving F, T, and R, as well as the driver’s budget B, find a \pi^* such that: 
\displaystyle \pi^* = \underset{\pi \in \Pi}{\arg \max}\ \mathcal{E}(\pi,\mathbf{F},\mathbf{T},\mathbf{R},B)

Driver strategies

A fully flexible driver, with complete freedom to choose their work schedule as well as to relocate to different zones has the most potential to maximise their income. Such a driver is said to follow a flexible relocation strategy. And it turns out we can find a solution to the Max Earnings problem for a driver following this strategy in O(n^2 N B) time (where N is the time horizon over which we want to optimise earnings, e.g. B=8 and N=24 for optimising 8 hours of work within a day). The solution is a dynamic programming recurrence – do your next driver a favour and scribble this on the back of a napkin for them 😉 :

In this equation, i_0 is the driver’s home zone, \Phi(i,b,t) is the total expected future earnings of a driver in zone i at time t with b budgeted time units remaining in their shift, and \mathbf{v}(i,b,t) is the vector of these cumulative earnings across different time zones j when a driver waits for a passenger in the current zone i at time t with b time units remaining.

According to driver preference, we might impose further restrictions on driver actions:

  • In a naive strategy, a driver performs a random walk over the city on weekdays from 9am-5pm, with locations dictated by passengers picked up and no relocations.
  • In the relocation strategy, a driver in a given zone can choose to either wait for a passenger or relocate (but not change working times).
  • In the flexible strategy a driver in a given zone can choose to either wait for a passenger or go home (pause working) — but not relocate. This strategy also naturally incorporates a common driver behaviour of working until a desired target earning has been reached, it will compute a schedule that minimises the (total) work time needed to reach a desired target earning.

Solving Max Earnings for the naive, the relocation, and the flexible strategies can be done by streamlined versions of the dynamic programming problem presented above; the details are omitted due to space constraints.

What happens when we don’t have perfect information?

It is possible to model the effects of noise in the information by considering a set of matrices within a certain input uncertainty threshold of the true matrix values. From this it is possible to compute the worst-case total expected earnings for a driver. The Robust Earnings problem finds the policy that leads to the minimum worst case.

… we can show (details omitted due to space constraints) that this problem can be solved by enhancing the total expected future earnings associated with Get Passenger in the dynamic programming routines with an optimization problem. We use an off-the-shelf minimizer…

(An extended version of the paper without the space constraints would be nice to see!).

Experimental results

So now to the fun stuff…

The dataset for the experiments is based on the NYC taxi dataset with data on over 200,000 taxi rides per day in 2015-16, enriched with data from the Uber API to give price estimates for the rides. Data from the Uber API was collected to recreate rides that occurred in the original dataset from October 2015 to March 2016.

The best options for fully flexible drivers

The following chart shows the daily drivers earnings that would have been obtained following different strategies.

The median earning of a driver following the naive strategy on a Sunday is $104 while that of a driver following flexible-relocation is $ 177, representing a 70% increase in median earnings. Averaged over all days of the week, this results in a 47% increase in median earnings per work day when following the flexible-relocation strategy.

Smart relocations through the day help a driver avoid becoming trapped in low-earning neighbourhoods. This turns out to beneficial even though it costs money to change zones when not carrying a passenger.

Uber’s surge pricing incentivises drivers to drive during peak hours in order to efficiently match demand with supply (and also has a demand-reducing effect from a passenger perspective). Should drivers chase surges?

The following chart compares a ‘no surge’ baseline with the surge multiplier taken out of the equation, a ‘surge’ case in which the surge multiplier is used when calculating earnings, a a ‘surge chasing’ case in which a driver in a non-surging zone always relocates to the zone with the highest surge multiplier within a 10-minute drive radius.

We observe that blind “surge chasing” leads to lower earnings irrespective of the strategy being followed… “surge chasing” consistently fails to provide any tangible benefits as compared to following the pre-determined strategy. We conclude that actively and blindly chasing the surge is an ill-advised strategy and may lead to losses.

When is relocation most effective

A comparison of the simulated behaviour of drivers following the flexible and flexible-relocation strategies highlights the times when relocation is most effective.

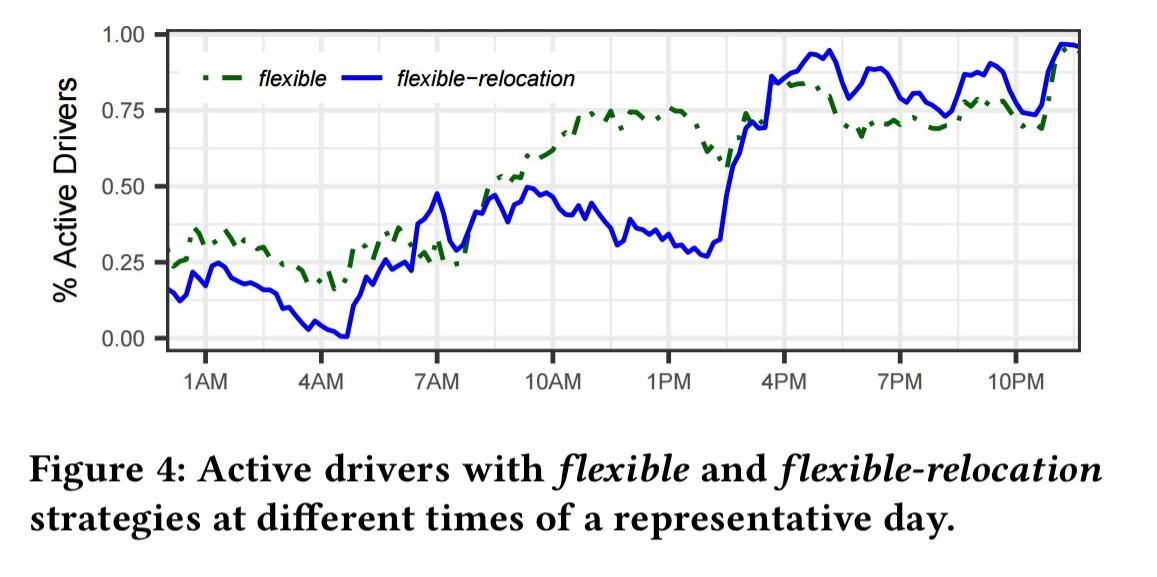
Here we can see (through the increased number of drivers choosing to drive then) that relocation is most effective in the evening hours.

The impact of flexible working hours

A comparison of the simulated behaviour of drivers following the relocation and flexible-relocation strategies highlights the differences in working zones when a driver is free to chose their own hours.

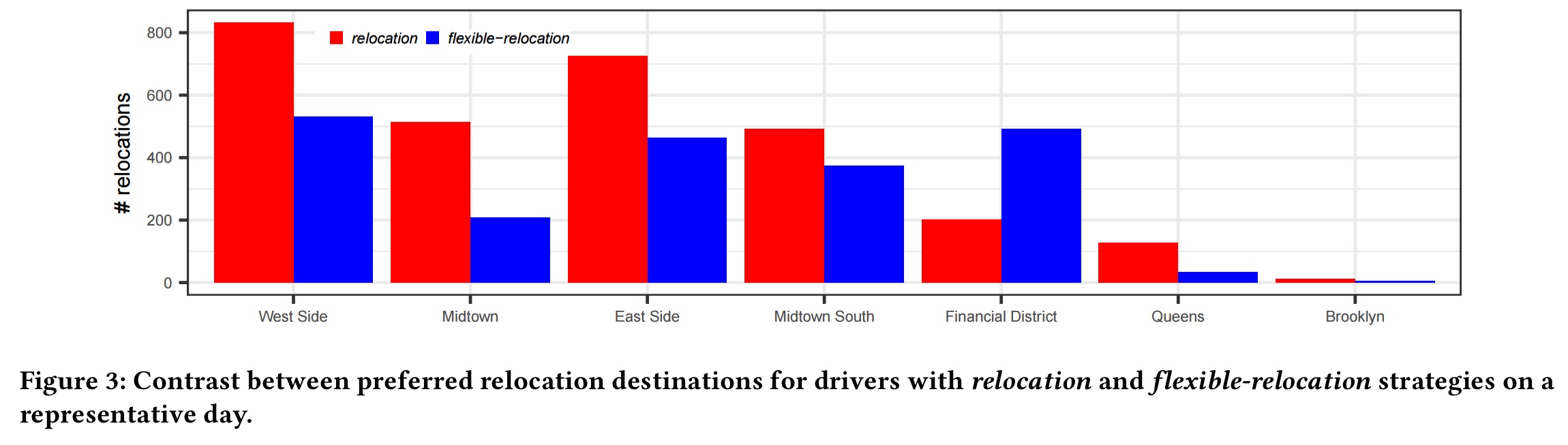
Without flexible relocation drivers mostly chose to serve the centre of Manhattan. With flexible hours, there is no clear most-preferred relocation zone.

Strategy robustness in the face of noise

…all strategies remain resilient to a wide range of additional uncertainty, and we find that the relocation, flexible, and flexible-relocation strategies are most tolerant to uncertainty in the input-transition matrices. Interestingly, even with 99% uncertainty, the flexible-relocation strategy significantly outperforms the naive strategy with no uncertainty.

Being strategic using historical data can significantly improve driver earnings.