A survey on dynamic and stochastic vehicle routing problems Ritzinger et al., International Journal of Production Research
It’s been a while since we last looked at an overview of dynamic vehicle routing problems: that was back in 2014 (See ‘Dynamic vehicle routing, pickup, and delivery problems’). That paper has fond memories for me, I looked at it while doing diligence for our investment in Deliveroo, and my how they’ve grown since then! With vehicle routing problems popping up in a number of interesting businesses, it’s time to take another look! Today’s paper choice is a more recent survey, focusing in on DSVRP problems.
So what exactly is a DSVRP problem? The VRP part stands for vehicle routing problems, typically you have a fleet of vehicles, and you need to use them to make a set of deliveries from point A to point B. How you assign pick-ups and deliveries to vehicles, and the routes those vehicles take, is the the VRP problem. Historically the VRP problem would be solved statically (we know up front the set of vehicles, pick-up and drop-off locations, etc.). Much more interesting (and much more realistic for many companies) is when we allow things to change over time. For example, customer requests come in during the day, traffic conditions change meaning that journey times are impacted, and so on. These are dynamic vehicle routing problems (DVRP). Then some bright spark had the insight that we can also learn from past data! That is, even though we don’t know in advance the exact conditions we’re likely to encounter, we can build predictive models that can inform our planning. This is the stochastic element. Put it all together and you have DSVRP: dynamic, stochastic vehicle routing.
In the last years, research interest in vehicle routing has increasingly focused on dynamic and stochastic approaches… The recent development in telematics, such as the widespread use of positioning services and mobile communication, allows gathering real-time information and exact monitoring of vehicles. This builds the basis for extensive data collection and real-time decision support in vehicle routing. Additionally, today’s computing capacity allows the application of routing algorithms which provide real-time solutions by incorporating online information and considering possible future events.
One of the interesting findings from this survey is the impact that different dynamic and stochastic elements can have on the performance of a routing algorithm. Compared to a static model:
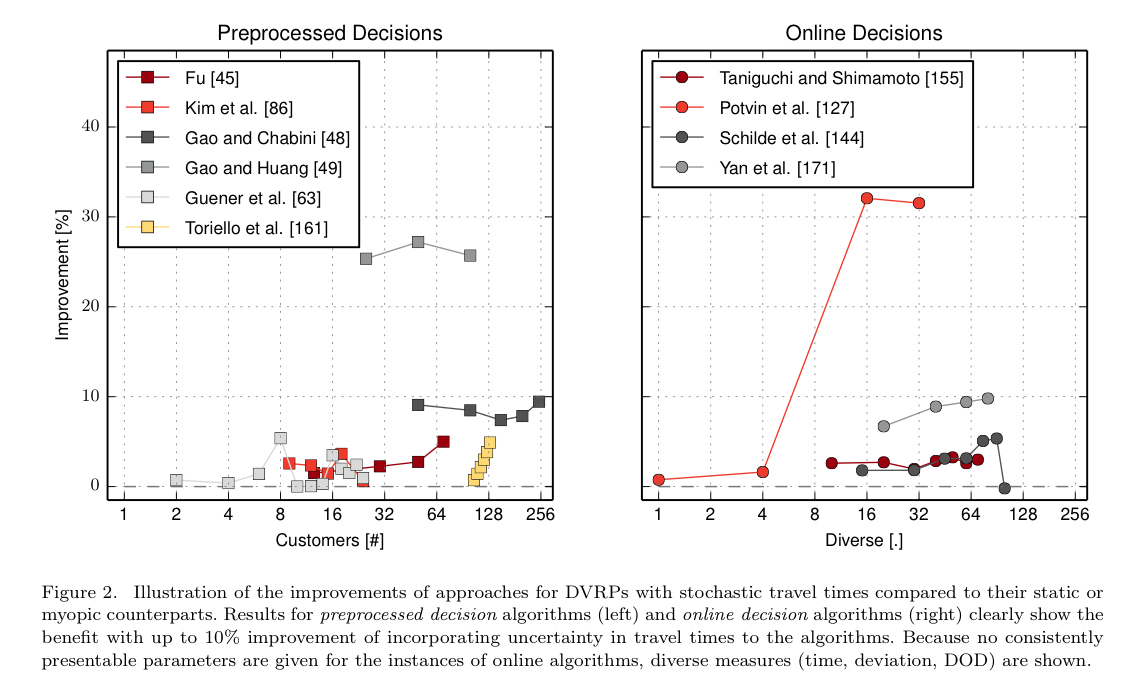
- Adding in consideration of travel time uncertainty gives improvements of up to 10%.
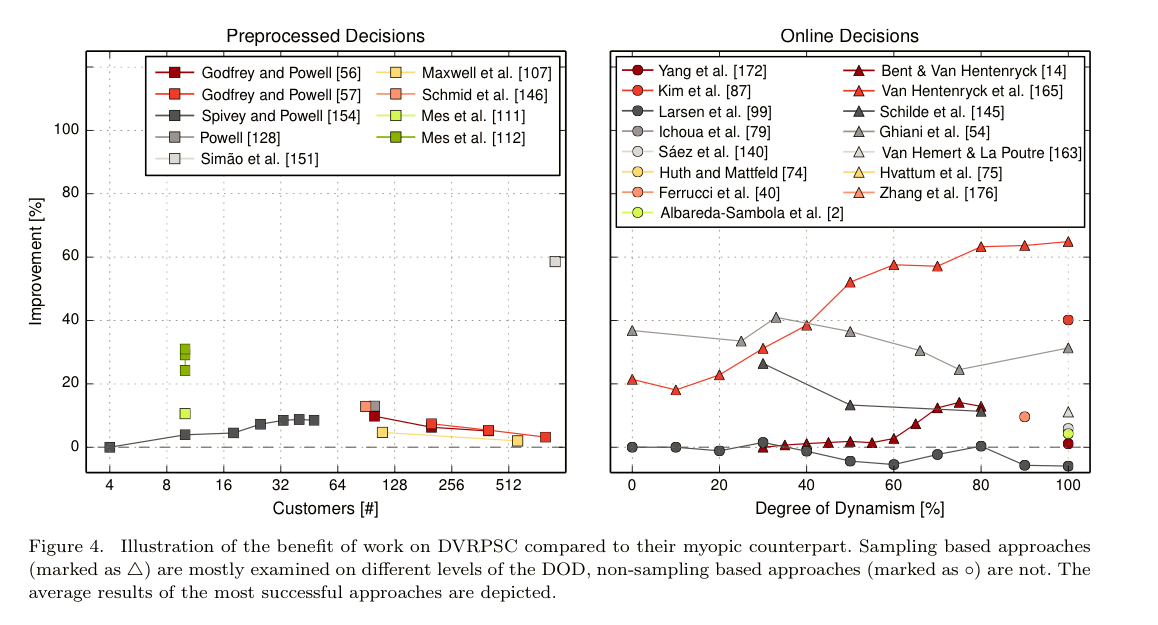
- When routes are known in advance, but customer demand at each stop is not known (e.g., supplying of gas stations, garbage collection), adding in online decisions (dynamic) can improve performance by around 30-40%
- When we consider dynamic customer requests, performance can be improved by up to 60%
In other words, invest your energy in building predictive models of customer demand first, and worry about incorporating dynamic information on traffic conditions afterwards.
Now, I waved my hands a little there in talking about the ‘performance’ of a routing algorithm. Setting up an appropriate objective function is in fact an interesting question in its own right. Are you optimising for minimum cost (e.g. by reducing travel time or distances), minimal response times, maximal revenue, number of serviced requests, percentage of requests met within some SLO, etc.?
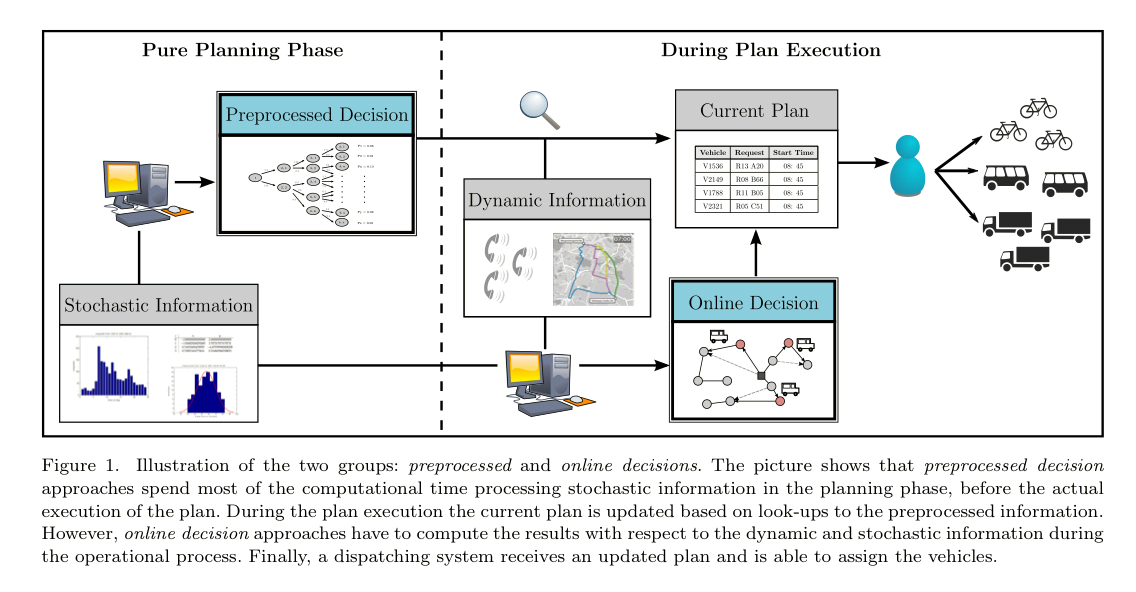
We can divide the class of DSVRP problems into two broad groups. The first group use preprocessed decisions. They use up front computation to work out ahead of time what the best course of action is to take in any given situation, and then choose from amongst those pre-computed alternatives at runtime as new information comes in. More interesting is the online decision group, which evaluate the best course of action dynamically. There are two basic ways of triggering re-computation here: in a time-driven approach we re-calculate at fixed time intervals; in an event-driven approach we re-calculate whenever a new event arises (aka rolling horizon or look ahead strategy). When an event arrives we take into account the new event information and the latest available stochastic information, and either make a single decision for the current situation, or a full re-optimised plan. A variation is to provide a quick greedy single decision, and schedule more intensive re-optimisations in the background. The best way to go is influenced by the degree of dynamism in the system, and the desired reaction time to new events.
Modelling travel times
There are three possible approaches to modelling changing travel times:
- The simplest model is time dependent (i.e., you have a simple lookup table for expected travel time at a given time of day)
- Then there are stochastic approaches modelling a distribution of travel times independent of time of day
- Finally, stochastic and time-dependent solutions model link travel times as random variables with time-dependent distributions.
These days I’d be tempted just to throw a neural network at it and learn a predictive model. Time of day would certainly be one of the input features.
Results show that a good strategy is to accept lateness in case of small deviations in travel times, but react on events of a large magnitude… the reliability (i.e., level of customer service) increases considerably when uncertainty in travel times is considered in the solution approach.
Modelling customer demand
Models for dynamic customer demand combine stochastic information about both customer locations and the time of request.
The aim is to appropriately react to new events by introducing rules that can be easily computed in real-time. These rules consider future events in the decision making process by generating scenarios of potential outcomes. A common concept, called sample scenario approach (SSA), is to generate multiple scenarios of future customer requests and include them in the planning process. After selection the most appropriate solution for the future, the sampled customers are removed but with the effect that the new solution is well prepared for possible future requests.
Incorporating very near future information in the planning process (short-term sampling) proves to be the most beneficial. Besides sampling, other strategies such as waiting strategies are also investigated (see e.g. ‘Putting data in the driver’s seat…’). For example, using a rolling horizon approach where geographical and temporal information about customer requests is exploited to reposition vehicles during idle times. Incorporating stochastic information about customer requests yields up to 60% improvements.
What about when both traffic conditions and customer demand vary over time?
Aka, the real world!
Almost all research on DSVRPs considers not more than one stochastic aspect. Only little work is performed on investigating the impact of incorporating multiple stochastic aspects, e.g. consideration of stochastic travel times and customers.
The following chart gives an indication of the volume of published papers investigating different aspects of the DSVRP problem over the years:
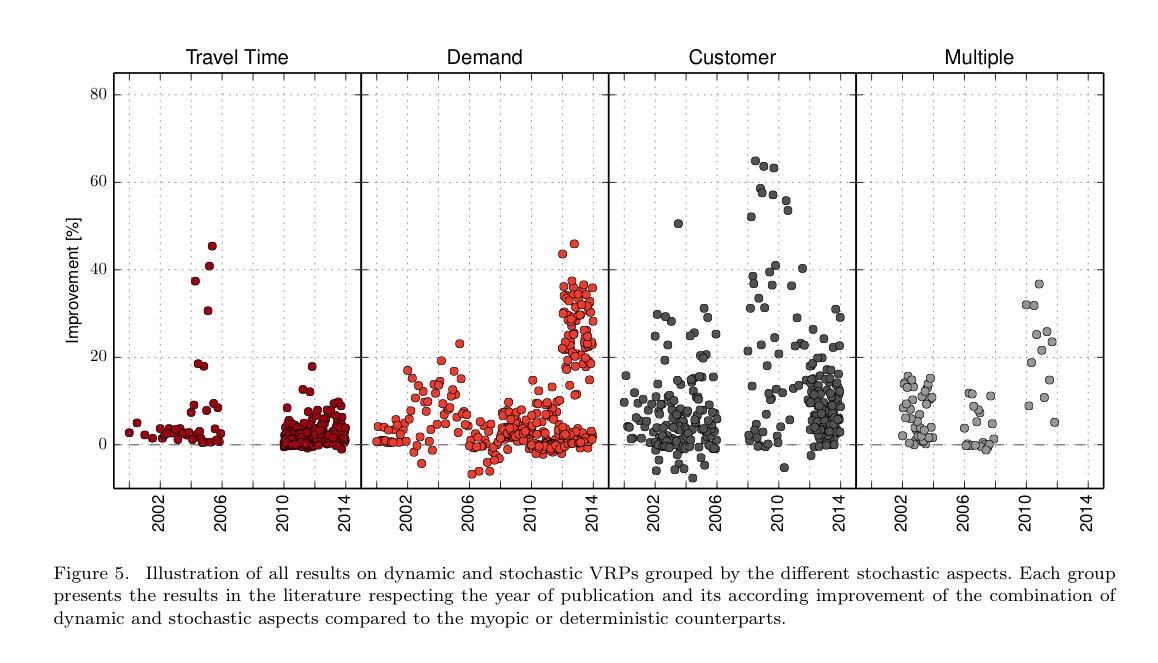
Papers considering multiple stochastic aspects are on the rise! Unfortunately, in addition to being an area less covered by research, it’s also less covered in this survey. It seems reasonable to assume that such approaches should yield improvements of up to at least 60%, since approaches considering only variations in customer demand do that well.
I can’t help but wonder if maybe there’s a radically different approach out there using end-to-end reinforcement learning. Given historical data about traffic and demand, we could replay a subsequence of the data and then ask the system to take a decision. We could then give that decision a score based on what we know about what happened next in the real-world… I’ve seen this ‘learning from sub-sequences’ tactic used in one of the previous papers that we’ve looked at on The Morning Paper, but right now I can’t for the life of me remember which one! Let me know if you find it :).