Efficient large-scale fleet management via multi-agent deep reinforcement learning

~ Adrian Colyer

Efficient large-scale fleet management via multi-agent deep reinforcement learning Lin et al., KDD’18

A couple of weeks ago we looked at a survey paper covering approaches to dynamic, stochastic, vehicle routing problems (DSVRPs). At the end of the write-up I mentioned that I couldn’t help wondering about an end-to-end deep learning based approach to learning policy as an alternative to the hand-crafted algorithms. Lenz Belzner popped up on Twitter to point me at today’s paper choice, which investigates exactly that.

The particular variation of DSVRP studied here is grounded in a ride-sharing platform with real data provided by Didi Chuxing covering four weeks of vehicle locations and trajectories, and customer orders, in the city of Chengdu. With the area covered by 504 hexagonal grid cells, the centres of which are 1.2km apart, we’re looking at around 475 square kilometers. The goal is to reposition vehicles in the fleet at each time step (10 minute intervals) so as to maximise the GMV (total value of all orders) on the platform. We’re not given information on the number of drivers, passengers, and orders in the data set (nor on the actual GMV, all results are relative), but Chengdu has a population of just under 9 million people and Didi Chuxing itself serves over 550M users across 400 cities, with 30M+ rides/day, so I’m guessing there’s a reasonable amount of data available.

One key challenge in ride-sharing platforms is to balance the demands and supplies, i.e., orders of the passengers and drivers available for picking up orders. In large cities, although millions of ride-sharing orders are served everyday, an enormous number of passenger requests remain unserviced due to the lack of available drivers nearby. On the other hand, there are plenty of available drivers looking for orders in other locations.

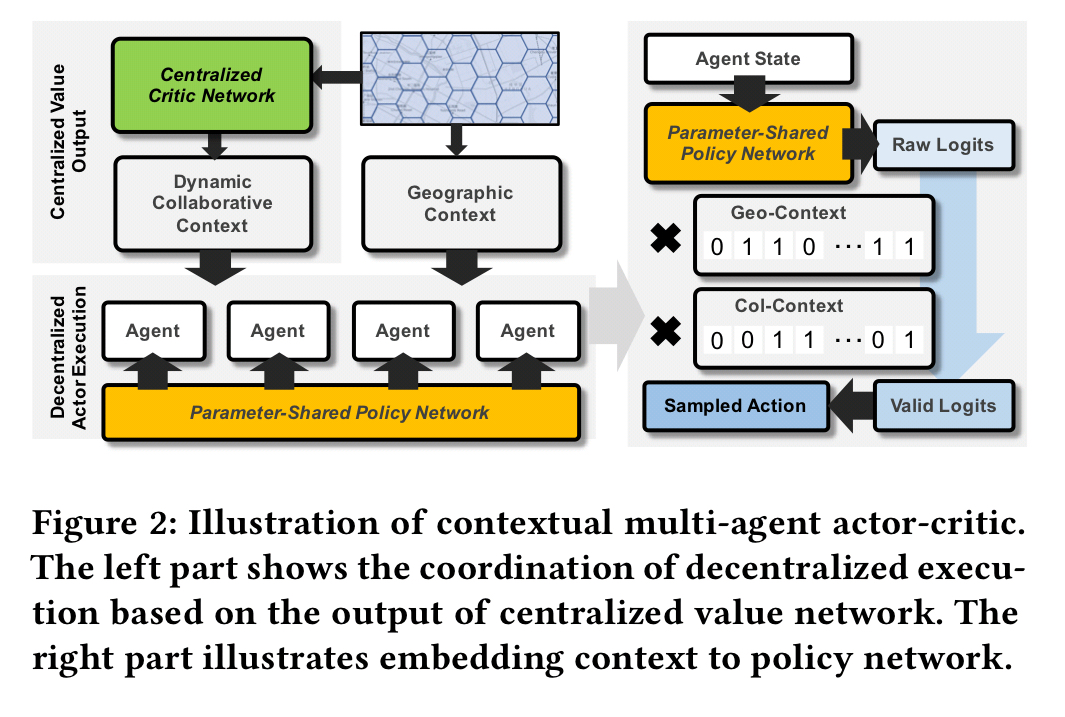
The authors propose to tackle this fleet management problem using deep reinforcement learning (DRL). For reinforcement learning to succeed we need a well defined agent, reward policy, and action space. If we go with a single ‘fleet management’ agent then the action space becomes intractably large (all the possible moves for all of the vehicles). So an alternative is to consider each vehicle as an agent, and formulate a multi-agent DRL problem. The challenge then becomes the effective training of many thousands of agents, with agents also arriving and leaving over time: “most existing studies only allow coordination among a small set of agents due to the high computational costs.” Furthermore, we need to find a way to coordinate the actions of the agents (it’s no good for example having every driver converge on the same location). To deal with all of this the authors introduce two contextual multi-agent reinforcement learning algorithms for multi-agent DRL: contextual multi-agent actor critic (cA2C) and contextual deep Q-learning (cDQN).

…DRL approaches are rarely seen to be applied in complicated real-world applications, especially in those with high-dimensional and non-stationary action space, lack of well-defined reward function, and in need of coordination among a large number of agents. In this paper, we show that through careful reformulation, DRL can be applied to tackle the fleet management problem.

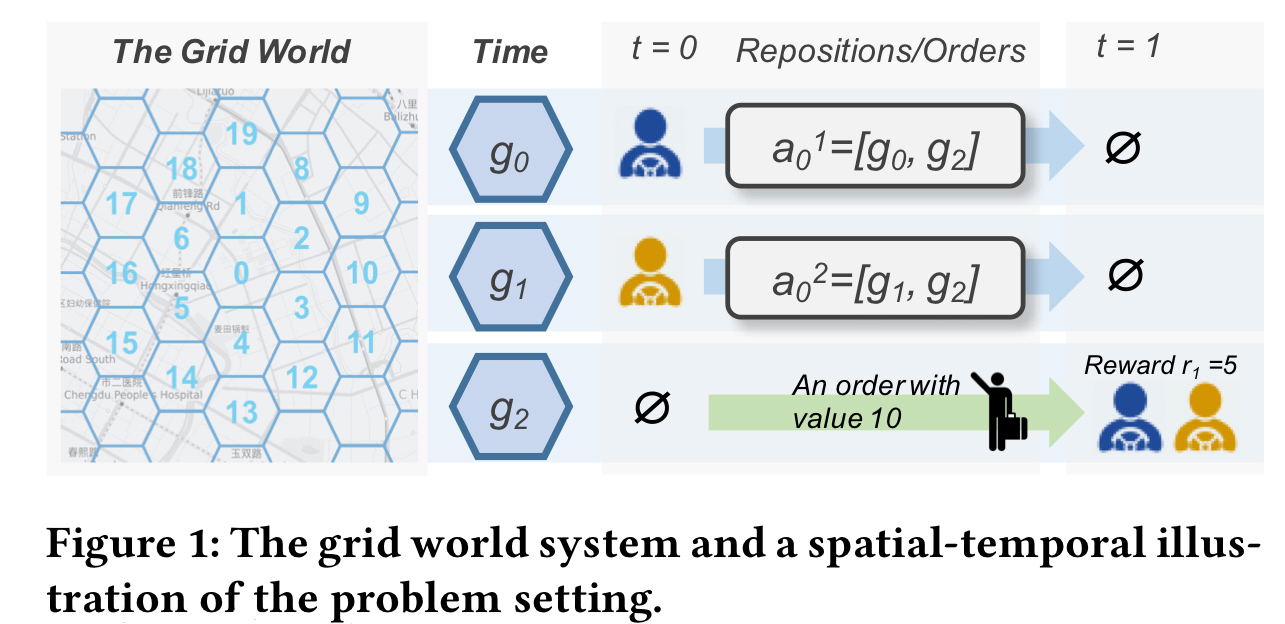
The problem is modelled as follows:

  • The map is overlaid with a hexagonal grid, with grid centers 1.2km apart.
  • The day is split into 144 10-minute intervals
  • In each time interval a given vehicle may move up to one grid cell in any direction (unless it’s on the edge of the grid, when choice may be further restricted). Thus an agent has up to 7 actions to choose from in each time step. At time t the joint action vector \mathbf{a}_t encodes the actions chosen by all agents through concatenation.
  • Orders emerge stochastically in the grid in each time interval, and are served by vehicles in the same or a neighbouring cell.
  • Global state \mathbf{s}_t is maintained comprising the numbers of vehicles and orders available in each grid cell, and the current time t. The state for a given agent is a concatenation of this global state plus a one-hot encoding of the current grid location of the agent (vehicle).
  • The state transition probability tells us the probability of arriving in a state \mathbf{s}_{t+1} given the current state \mathbf{s}_t and the joint action vector. The actions are of course deterministic, but there are also stochastic elements due to new vehicles coming online, existing vehicles going offline, and new orders arriving.
  • The reward function for an agent maps a state and action to a reward score. All agents in the same location share the same reward function. Each agent attempts to maximise its own expected discounted return. The reward for an agent a is based on the averaged revenue of all agents arriving at the same grid cell as a in the next time step.

Such a design of rewards aims at avoiding greedy actions that send too many agents to locations with high volumes of orders, and aligns the maximization of each agent’s return with the maximization of GMV.

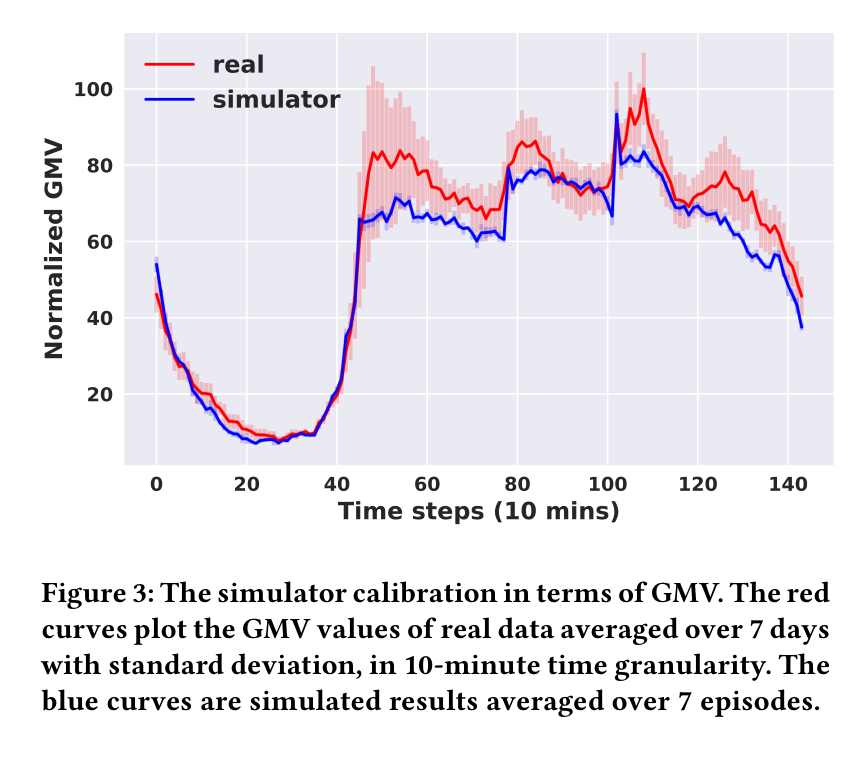
The policies of the agents are evaluated and trained in a simulator informed by the Didi Chuxing dataset that performs the following steps in each time step:

  1. Update vehicle status (setting some offline, and bringing some new vehicles online)
  2. Generate new orders
  3. Interact with the agents, passing the new global state and receiving the agent actions
  4. Assign available orders through a two-stage procedure: first the orders in a given grid cell are assigned to vehicles in the same cell, then the remaining unfulfilled orders are assigned to vehicles in neighbouring cells.

Following calibration, the GMV reported by the simulator follows very closely the real data from the ride-sharing platform.

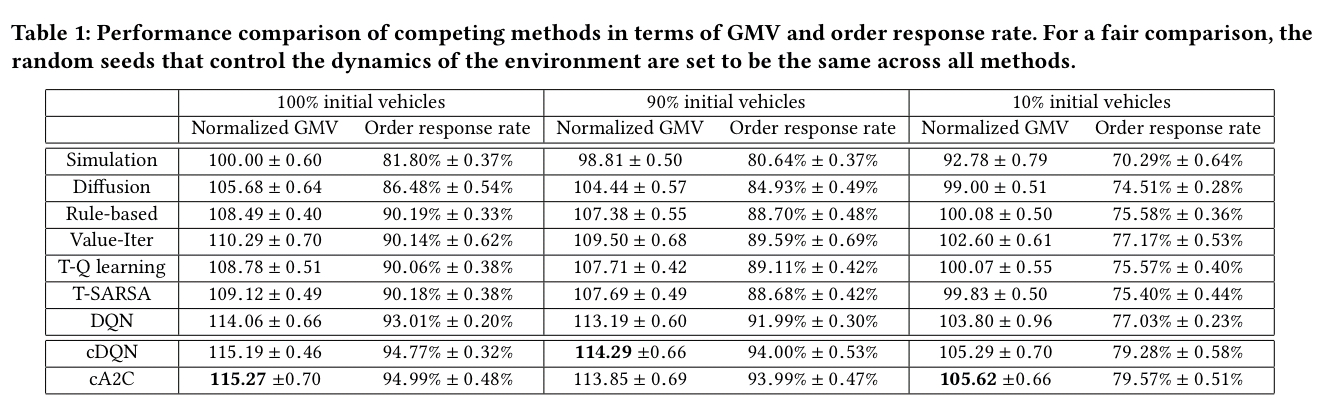
Within this context, cA2C and cDQN are two independently developed algorithms that are compared against each other (and to a number of other baselines) in the evaluation. Depending on the number of vehicles assumed to be initially online, cDQN and cA2C both give up to a 15% uplift in GMV over an unmanaged baseline (denoted ‘simulation’ in the table below), and increase the percentage of orders fulfilled from around 82% to 95%.

(Enlarge)

The algorithms

Contextual DQN shares network parameters across all agents, and distinguishes them with their ids. For the reward function, a key observation is that all actions which leave a vehicle in some grid cell g must share the same action value (regardless of action). So there are only N unique action values (for N grid cells). That follows straightforwardly from the averaged revenue definition of the reward function. This simplifies the optimisation and also provides the foundation of a coordination mechanism for agent collaboration.

There are two further constraints / inputs. First, a geographic context \mathbf{G}_{g_{j}} \in \mathbb{R}^7 is used to filter out invalid actions for an agent in grid location \mathbf{g}_j. This addresses edge locations, and other impassable interior grid cells (e.g., lakes). Secondly we want to avoid needless movement, as would occur for example if an agent in location 1 moved to location 2 in the same time step as an agent from location 2 moved to location 1. A collaborative context input \mathbf{C}_{t,g_j} \in \mathbb{R}^7 encodes this constraint by further restricting the valid actions for an agent: an agent can only move to a grid location with a high action value than their current location.

Contextual Actor-Critic is a contextual multi-agent actor-critic algorithm.

There are two main ideas in the design of cA2C: 1) A centralized value function shared by all agents with an expected update; 2) Policy context embedding that establishes explicit coordination among agents, enables faster training and enjoys the flexibility of regulating policy to different action spaces.

Coordination is again achieved by masking the available actions based on the geographic and collaborative contexts.

Comparing models with (cA2C v3) and without (cA2C) the collaborative context component shows that it is indeed effective in reducing conflicts and improving GMV.

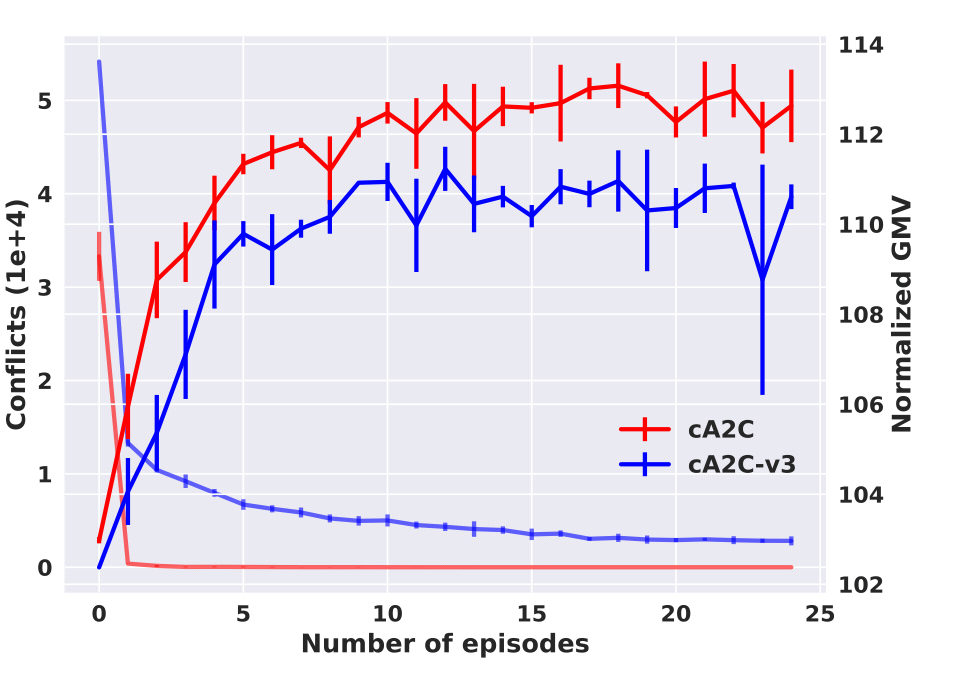
Note that the collaboration doesn’t involve any true communication between the agents, it’s more an emergent property of the constraints in the shared state space.

In action

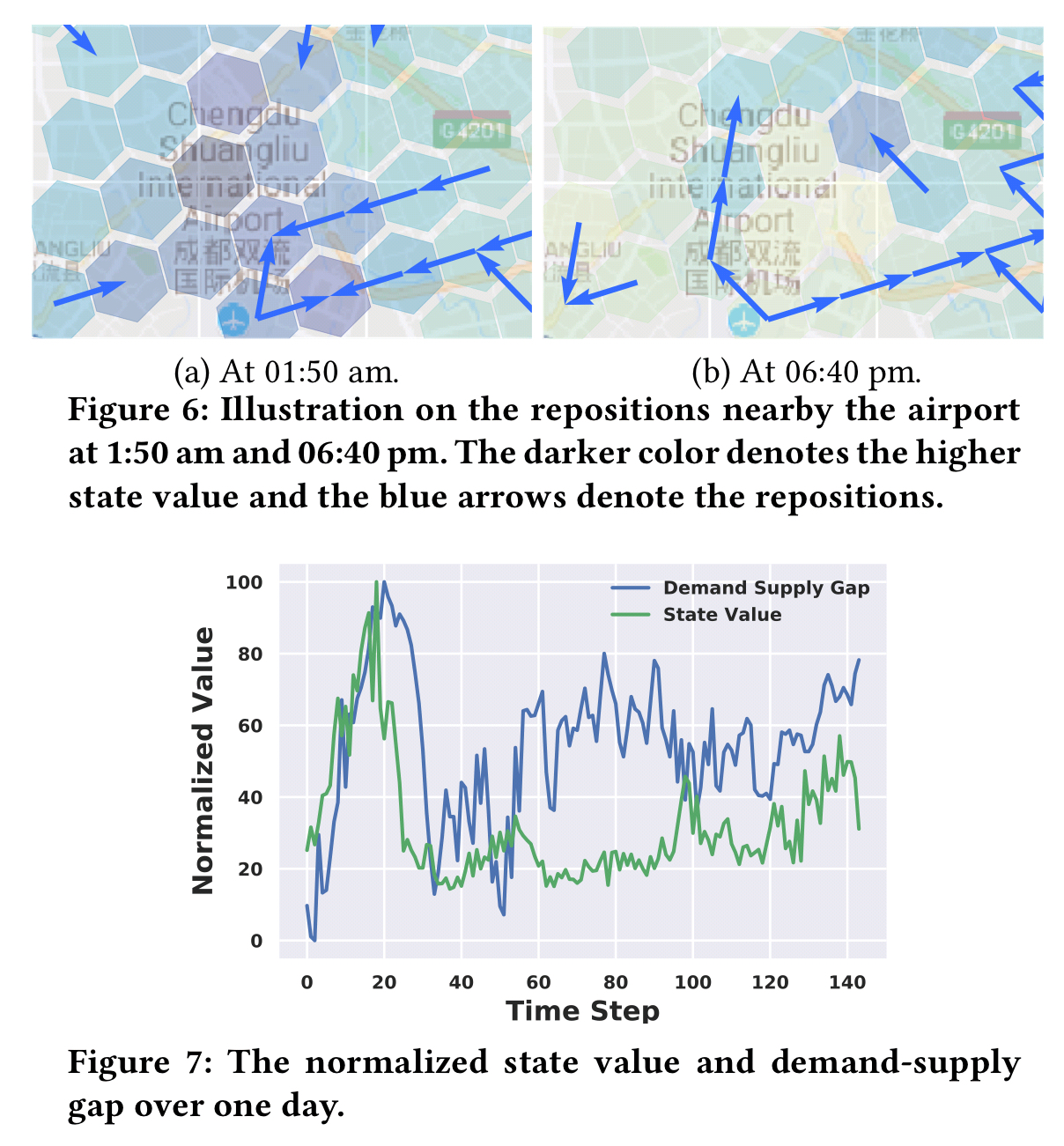
There’s a nice worked example at the end of the paper (§6.6) illustrating how the network learns demand-supply gaps and is able to reposition vehicles effectively. Here we’re looking at the region around the airport. After midnight there are a lot of orders and less available vehicles, so the ‘value’ of the airport grid cells increases and vehicles are moved towards it. During the early evening there are more vehicles available and the state values are lower. Vehicles also move to other locations.

…both cDQN and cA2C achieve large scale agents’ coordination in the fleet management problem. cA2C enjoys both flexibility and efficiency by capitalizing on a centralized value network and decentralized policy execution embedded with contextual information.