Mastering the game of Go without human knowledge Silver et al., Nature 2017
We already knew that AlphaGo could beat the best human players in the world: AlphaGo Fan defeated the European champion Fan Hui in October 2015 (‘Mastering the game of Go with deep neural networks and tree search’), and AlphaGo Lee used a similar approach to defeat Lee Sedol, winner of 18 international titles, in March 2016. So what’s really surprising here is the simplicity of AlphaGo Zero (the subject of this paper). AlphaGoZero achieves superhuman performance, and won 100-0 in a match against the previous best AlphaGo. And it does it without seeing a single human game, or being given any heuristics for gameplay. All AlphaGo Zero is given are the rules of the game, and then it learns by playing matches against itself. The blank slate, tabula rasa. And it learns fast!
Surprisingly, AlphaGo Zero outperformed AlphaGo Lee after just 36 hours; for comparison, AlphaGo Lee was trained over several months. After 72 hours, we evaluated AlphaGo Zero against the exact version of AlphaGo Lee that defeated Lee Sedol, under the 2 hour time controls and match conditions as were used in the man-machine match in Seoul. AlphaGo Zero used a single machine with 4 Tensor Processing Units (TPUs), while AlphaGo Lee was distributed over many machines and used 48 TPUs. AlphaGo Zero defeated AlphaGo Lee by 100 games to 0.
That comes out as superior performance in roughly 1/30th of the time, using only 1/12th of the computing power.
It’s kind of a bittersweet feeling to know that we’ve made a breakthrough of this magnitude, and also that no matter what we do, as humans we’re never going to be able to reach the same level of Go mastery as AlphaGo.
AlphaGo Zero discovered a remarkable level of Go knowledge during its self-play training process. This included fundamental elements of human Go knowledge, and also non-standard strategies beyond the scope of traditional Go knowledge.
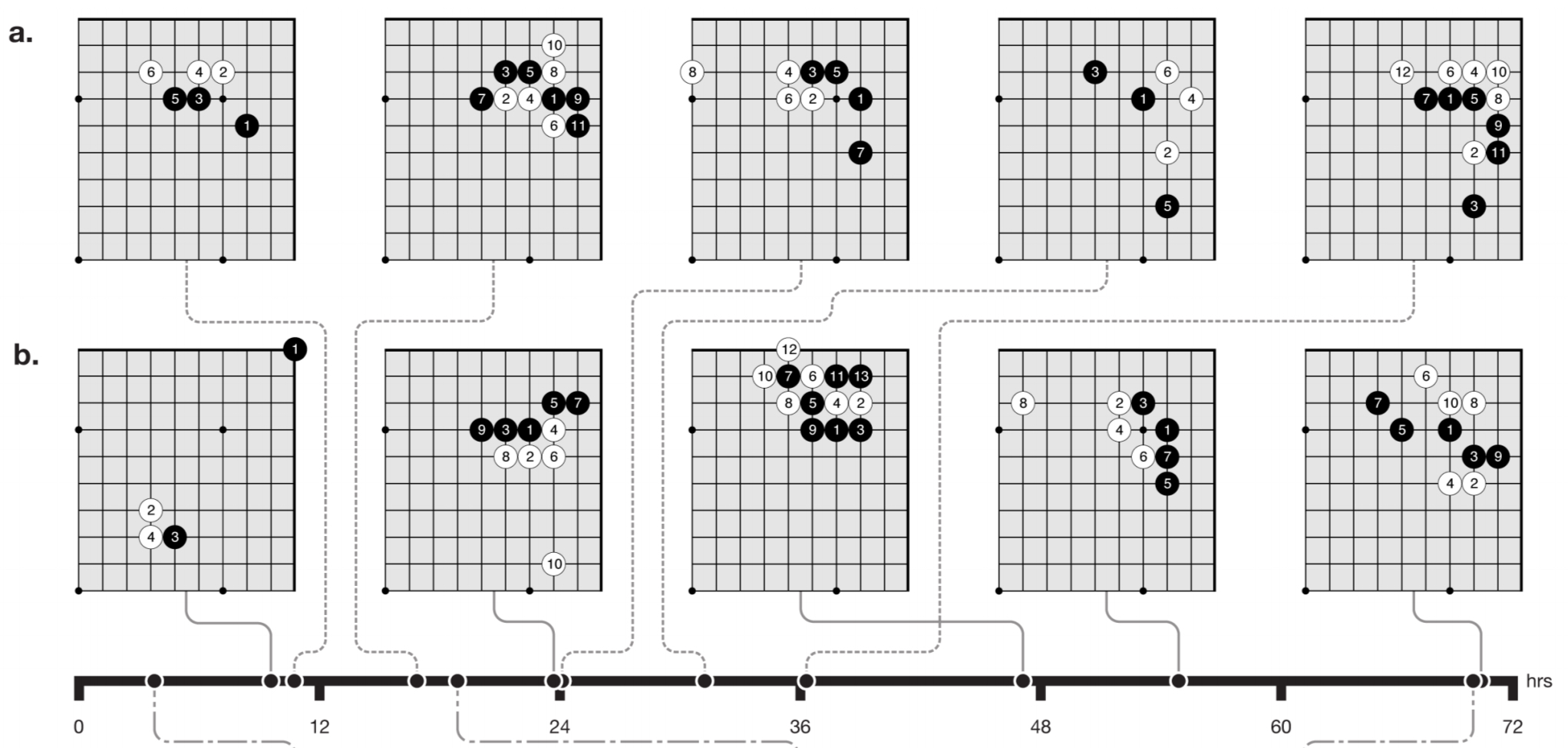
In the following figure, we can see a timeline of AlphaGo Zero discovering joseki (corner sequences) all by itself. The top row (a) shows joseki used by human players, and when on the timeline they were discovered. The second row (b) shows the joseki AlphaGo Zero favoured at different stages of self-play training.
At 10 hours a weak corner move was preferred. At 47 hours the 3-3 invasion was most frequently played. This joseki is also common in human professional play; however AlphaGo Zero later discovered and preferred a new variation.
Here’s an example self-play game after just three hours of training:
AlphaGo Zero focuses greedily on capturing stones, much like a human beginner. A game played after 19 hours of training exhibits the fundamentals of life-and-death, influence and territory:
Finally, here is a game played after 70 hours of training: “the game is beautifully balanced, involving multiple battles and a complicated ko fight, eventually resolving into a half-point win for white.”
On an Elo scale, AlphaGo Fan achieves a rating of 3,144, and AlphaGo Lee achieved 3,739. A fully trained AlphaGo Zero (40 days of training) achieved a rating of 5,185. To put that in context, a 200-point gap in Elo rating corresponds to a 75% probability of winning.
Our results comprehensively demonstrate that a pure reinforcement learning approach is fully feasible, even in the most challenging of domains: it is possible to train to superhuman level, without human examples or guidance, given no knowledge of the domain beyond basic rules.
How does AlphaGo Zero work?
There are four key differences between AlphaGo Zero and AlphaGo Fan/Lee, and we’ve already seen two of them:
- It is trained solely by self-play reinforcement learning, starting from random play.
- It uses only the black and white stones from the board as input features.
- It uses a single neural network rather than separate policy and value networks.
- It uses a simpler tree search that relies upon this single neural network to evaluate positions and sample moves, without performing any Monte-Carlo rollouts.
To achieve these results, we introduce a new reinforcement learning algorithm that incorporates lookahead search inside the training loop, resulting in rapid improvement and precise and stable learning.
From a human perspective therefore we might say that AlphaGo Zero achieves mastery of the game of Go through many hours of deliberate practice.
In AlphaGo Fan there is a policy network that takes as input a representation of the board and outputs a probability distribution over legal moves, and a separate value network that takes as input a representation of the board and outputs a scalar value predicting the expected outcome of the game if play continued from here.
AlphaGo Zero combines both of these roles into a single deep neural network that outputs both move probabilities and an outcome prediction value:
. The input to the network,
, consists of 17 binary feature planes:
. Each
and
input is a 19×19 matrix where
(
) if intersection
contains a stone of the player’s colour at time step
. The final input feature
is 1 if it is black’s turn to play, and 0 for white.
History features
are necessary because Go is not fully observable solely from the current stones, as repetitions are forbidden; similarly, the colour feature C is necessary because the komi is not observable.
The input is connected to a ‘tower’ comprised of one convolutional block and then nineteen residual blocks. On top of the tower are two ‘heads’: a value head and a policy head. End to end it looks like this:
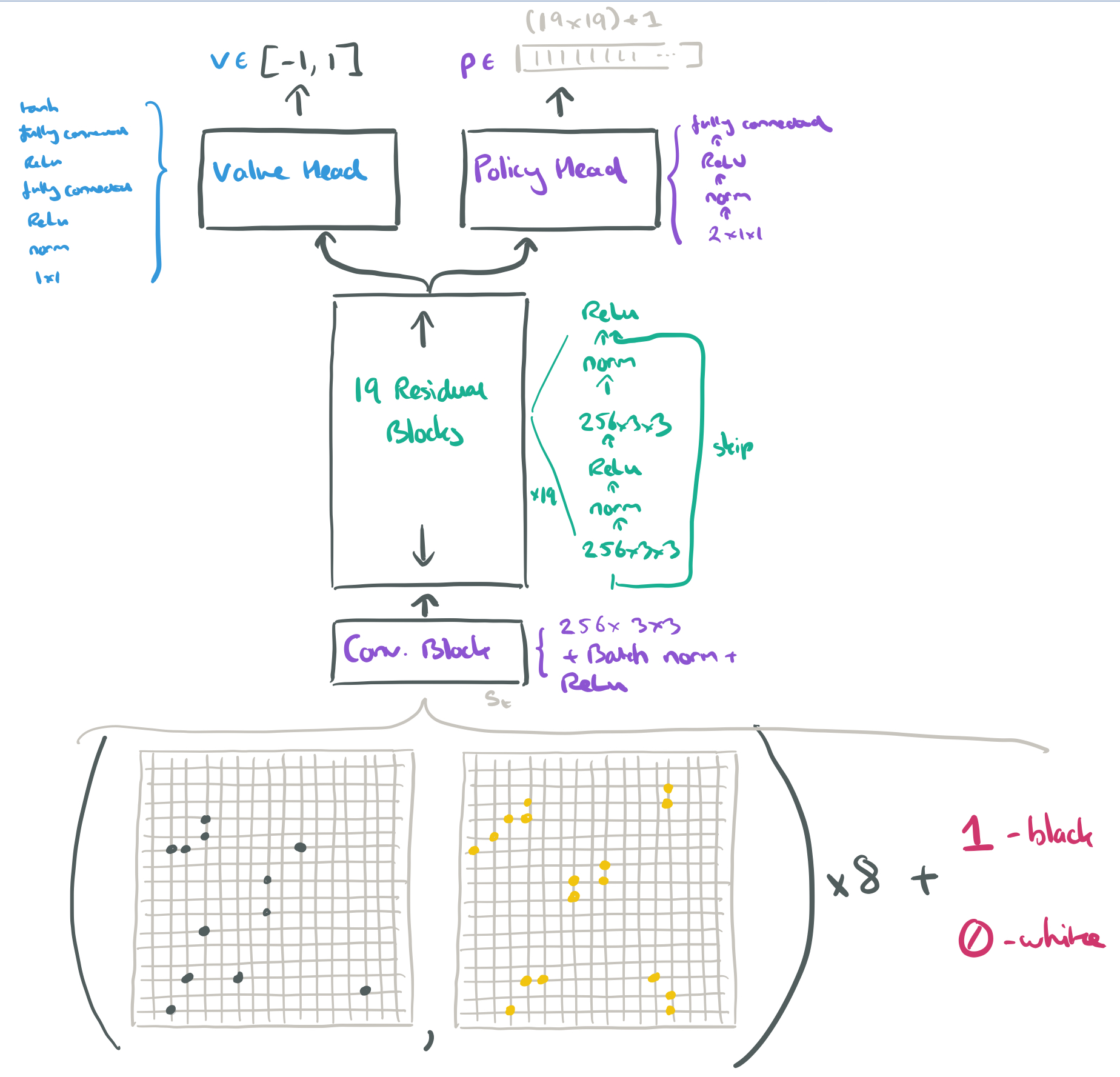
In each position , a Monte-Carlo Tree Search (MCTS) is executed, which outputs probabilities
for each move. These probabilities usually select much stronger moves than the raw move probabilities
of the policy head on its own.
MCTS may be viewed as a powerful policy improvement operator. Self-play with search — using the improved MCTS-based policy to select each move, then using the game winner
as a sample of the value — may be viewed as a powerful policy evaluation operator. The main idea of our reinforcement learning algorithm is to use these search operators repeatedly in a policy iteration procedure: the neural network’s parameters are updated to make the move probabilities and value
more closely match the improved search probabilities and self-play winner
; these new parameters are used in the next iteration of self-play to make the search even stronger.
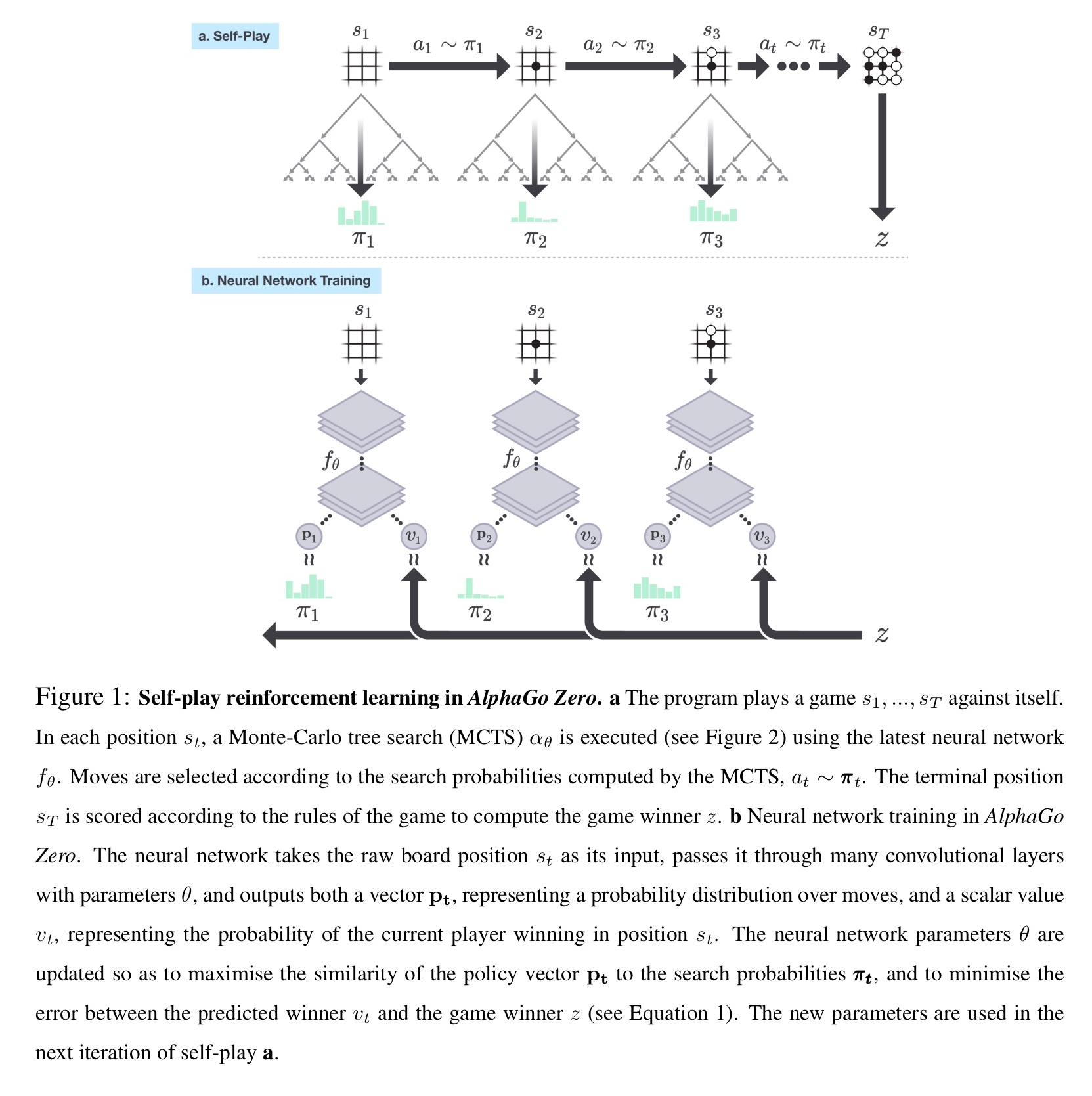
The nework is initialised to random weights, and then in each subsequent iteration self-play games are generated. At each time step an MCTS search is executed using the previous iteration of the network, and a move is played by sampling the search probabilities . A game terminates when both players pass, when the search value drops below a resignation threshold, or when the game exceeds a maximum length. The game is then scored to give a final reward.
The neural network
is adjusted to minimise the error between the predicted value
and the self-play winner
, and to maximise the similarity of the neural network move probabilities
to the search probabilities
. Specifically, the parameters
are adjusted by gradient descent on a loss function
that sums over mean-squared error and cross-entropy losses:
I’ll leave you to reflect on this closing paragraph, thousands of years of collective human effort surpassed from scratch in just a few days:
Humankind has accumulated Go knowledge from millions of games played over thousands of years, collectively distilled into patterns, proverbs, and books. In the space of a few days, starting tabula rasa, AlphaGo Zero was able to rediscover much of this Go knowledge, as well as novel strategies that provide new insights into the oldest of games.