Mastering the Game of Go with Deep Neural Networks and Tree Search Silver, Huang et al., Nature vol 529, 2016
Pretty much everyone has heard about AlphaGo’s tremendous Go playing success beating the European champion by 5 games to 0. In all the excitement at the time, less was written about how AlphaGo actually worked under the covers. Today’s paper choice is a real treat since it gives that us that inside look, and by virtue of being published in Nature, explains things in a way that makes them accessible to a broader audience than just deep learning specialists.
The game of Go has long been viewed as the most challenging of classic games for artificial intelligence due to its enormous search space and the difficulty of evaluating board positions and moves. We introduce a new approach to computer Go that uses value networks to evaluate board positions and policy networks to select moves.
The scale of the challenge
In theory Go is a game of perfect information and a search tree containing bd sequences of moves, where b is the game’s breadth (number of legal moves per position), and d is it depth (games) should tell us the perfect play in each position. Unfortunately, for Go b is around 250, and d is around 150. Exhaustive search is not possible!
Solution overview
There are two basic tactics we can use to make the problem more tractable: reduce the depth of the tree, and/or reduce the breadth of the tree.
The depth of the search may be reduced by position evaluation: truncating the search tree at state s and replacing the subtree below s b an approximate value function that predicts the outcome from state s.
We can reduce the breadth of the tree by sampling actions from a policy that is a probability distribution over possible moves in a given position.
Monte-Carlo rollouts search to maximum depth without branching at all, by sampling long sequences of actions for both players from a policy p. Averaging over such rollouts can provide an effective position evaluation, achieving super-human performance in backgammon and Scrabble, and weak amateur level play in Go.
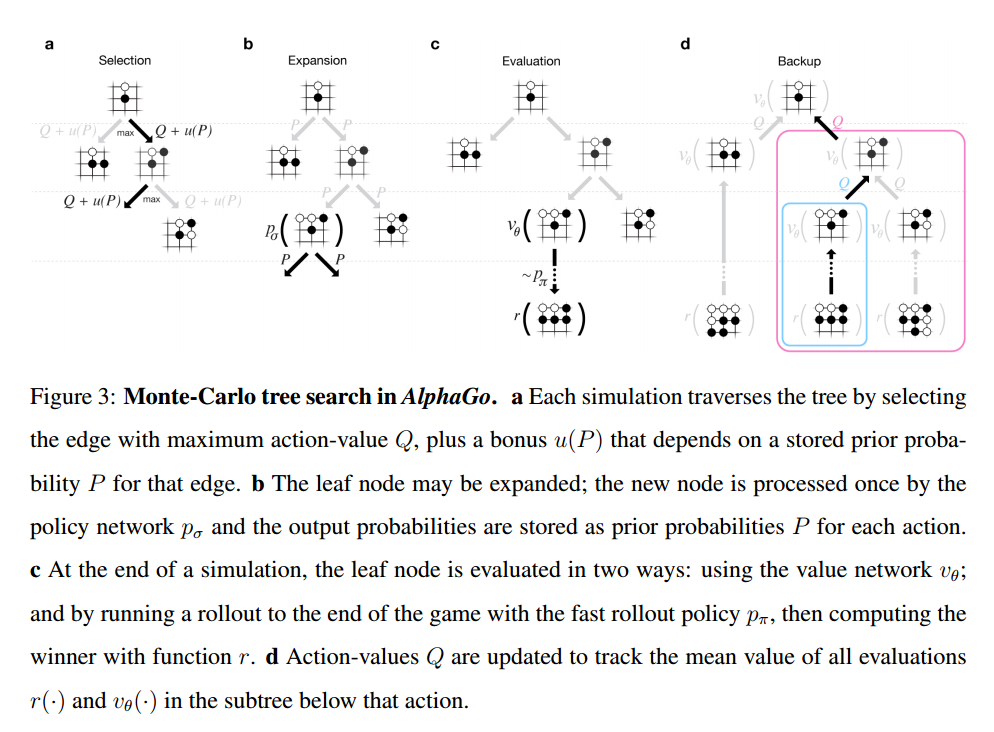
A Monte-Carlo tree search (MCTS) uses Monte-Carlo rollouts to estimate the value of each state in the search tree. The more simulations you do, the more accurate the values become…
The policy used to select actions during search is also improved over time, by selecting children with higher values. Asymptotically, this policy converges to optimal play, and the evaluations converge to the optimal value function. The strongest current Go programs are based on MCTS…
AlphaGo uses deep neural networks to learn a value network used to reduce search depth, and a policy network used to reduce search breadth. The board is expressed as a 19×19 image and convolutional layers are used to construct a representation of the position that becomes the input to these networks. AlphaGo combines the policy and value networks with MCTS to construct the final gameplay engine.
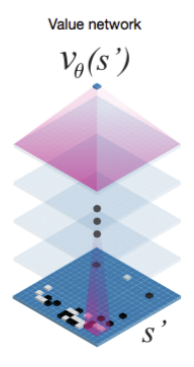
The policy network takes a representation of the board, passes it through the convolutional layers, and outputs a probability distribution over legal moves:
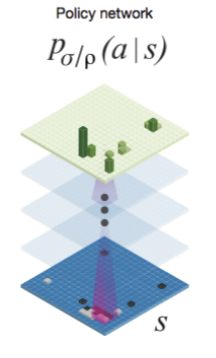
The value network also passes the board representation through convolutional layers, and outputs a scalar value predicting the expected outcome.
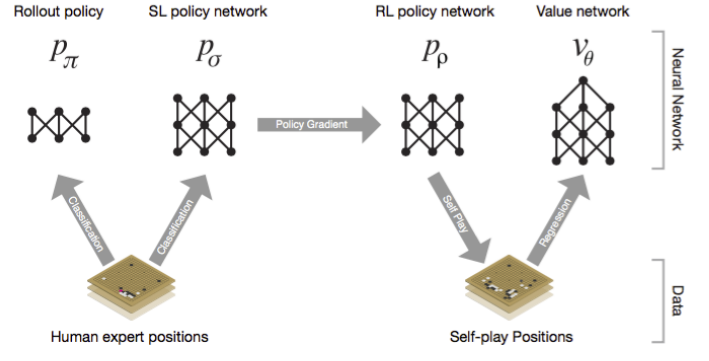
The neural networks are trained used a 3 stage pipeline:
- A supervised learning policy network is trained directly from expert human moves.
- A reinforcement learning policy network improves upon the network from stage one by playing games against itself. “This adjusts the policy towards the correct goal of winning games, rather than maximising predictive accuracy.”
- A value network is trained to predict the winner of games played by the RL policy network of stage 2 against itself.
Training stage 1: Supervised learning
A 13-layer policy network was trained from 30 million positions. The network alternates between convolutional layers and rectifier non-linearities. A final softmax layer outputs the probability distribution over all legal moves. The network predicted expert moves with an accuracy of 57%, and small improvements in accuracy led to large improvements in playing strength.
In addition, a faster but less accurate rollout policy network was trained using a linear softmax of small pattern features. It achieved 24.2% accuracy, but was able to select a move in 2μs rather than 3ms for the policy network.
Training stage 2: Reinforcement learning through game play
The RL network is identical in structure to the SL network from stage one, with weights initialised to the same values. Games are played between the policy network and randomly selected previous iterations of the policy network.
When played head-to-head, the RL policy network won more than 80% of games against the SL policy network. We also tested against the strongest open-source Go program, Pachi, a sophisticated Monte-Carlo search program, ranked at 2 amateur dan on KGS, that executes 100,000 simulations per move. Using no search at all, the RL policy network won 85% of games against Pachi. In comparison, the previous state-of-the-art, based only on supervised learning of convolutional networks, won 11% of games against Pachi and 12% against a slightly weaker program Fuego.
Training stage 3: Reinforcement learning for position evaluation
Ideally we’d like to know the value function under perfect play, but the closest we can get is to estimate it using the RL policy network from stage 2.
We generated a new self-play dataset consisting of 30 million distinct positions, each sampled from a separate game. Each game was played between the RL policy network and itself until the game terminated.
A single evaluation of the trained function approached the accuracy of Monte-Carlo rollouts using the RL policy network, but using 15,000 times less computation.
Your move!
AlphaGo combines the policy and value networks in an MCTS algorithm that selects actions by lookahead search. Figure 3 in the paper provides a very clear illustration of how this works:
(Click for larger view).
How good?
We know that AlphaGo beat the European Go champion 5-0 using a distributed version of AlphaGo with 40 search threads, 1202 CPUs, and 176 GPUs. A single machine version of AlphaGo is still many dan ranks stronger than any previous Go program – winning 494 out of 495 games against other leading Go programs.
What next?
Go is exemplary in many ways of the difficulties faced by artificial intelligence: a challenging decision-making task; an intractable search space; and an optimal solution so complex it appears infeasible to directly approximate using a policy or value function. The previous major breakthrough in computer Go, the introduction of Monte-Carlo tree search, led to corresponding advances in many other domains: for example general game-playing, classical planning, partially observed planning, scheduling, and constraint satisfaction. By combining tree search with policy and value networks, AlphaGo has finally reached a professional level in Go, providing hope that human-level performance can now be achieved in other seemingly intractable artificial intelligence domains.