Reducing controversy by connecting opposing views

Reducing controversy by connecting opposing views Garimella et al., WSDM 2017

Society is often polarized by controversial issues that split the population into groups with opposing views. When such issues emerge on social media, we often observe the creation of ‘echo chambers’, i.e., situations where like-minded people reinforce each other’s opinion, but do not get exposed to the views of the opposing side. In this paper we study algorithmic techniques for bridging these chambers, and thus reduce controversy.

This is the follow-up to the paper on detecting controversial topics that we looked at yesterday. Suppose we find a controversial topic, and have the partitioned graph showing the two sides of the discussion, what can we do to bring them together? Adding edges (bridges) between users on opposite sides of the debate would reduce the controversy, and we can calculate (by looking at the impact on the RWC score) which edges we can add to have the greatest effect. Recall however that the graph is based on retweets and follows, so to ‘add an edge’ we need not only to make recommendations (e.g., to a recommendation to follow someone on the other side of the debate), but we also need users to act on those recommendations…

Clearly, some bridges are more likely to materialize than others. For instance, people in the ‘center’ might be easier to convince that people on the two extreme ends of the political spectrum. we take this issue into account by modeling an acceptance probability for a bridge as a separate component of the model.

Let’s ignore the acceptance probability issue temporarily so that we can focus on the simpler problem to start with. Graphs of controversial topics often have a structure that resembles star-graphs – a small number of highly popular vertices receiving incoming.

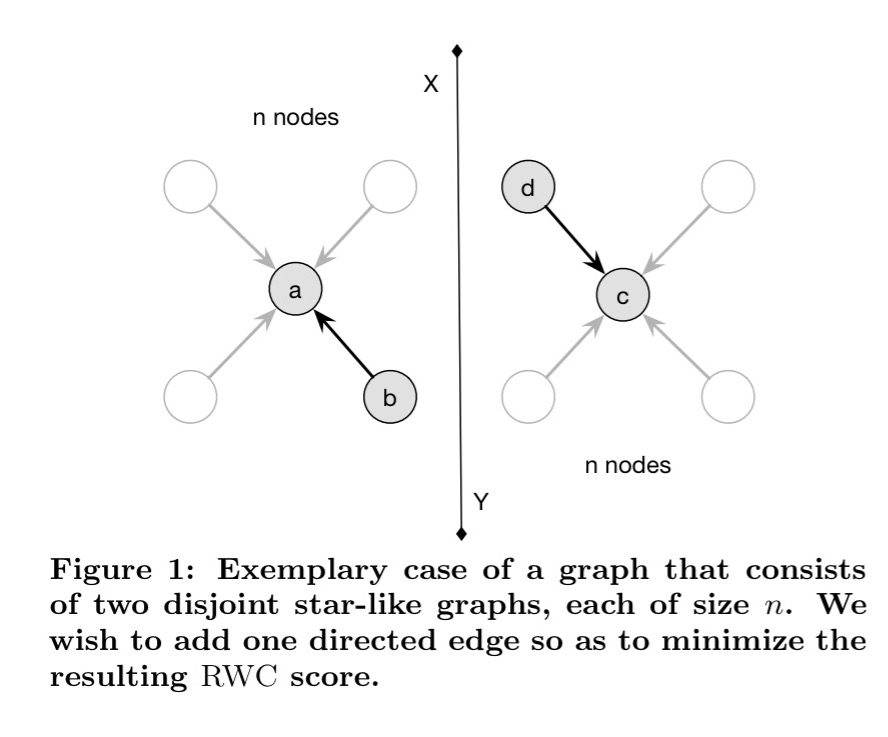
Connecting the centres of the two stars provides the maximum reduction in RWC score. More generally, the controversy reduction algorithm considers only edges between high-degree vertices on each side. For each of these candidate edges, the RWC score is calculated with the edge added. The k edges that lead to the lowest score when added to the graph individually then become the recommendations.

Adding back in the notion of acceptance probability, we need to calculate the expected RWC score for adding an edge, under some probabilistic model providing the probability the edge will be accepted once recommended.

We build such an acceptance model on the feature of user polarity [that we looked at yesterday]. Intuitively, this polarity score of a user, which takes values in the interval [-1,1], captures how much the user belongs to either side of the controversy… We employ user polarity as feature for our acceptance model because, intuitively, we expect users from each side to accept content from different sides with different probabilities, and wes assume these probabilities are encoded in, and can be learned from, the graph structure itself.

Let $P_u$ be the polarity score of user u (we’ll come back to how that is calculated in a moment). Then the probability $p(u,v)$ that user u accepts a recommendation to connect to user v is given by:

$N_{endorsed}(P_u,P_v)/N_{exposed}(P_u,P_v)$

That is, the fraction of times a user with polarity ~ $P_v$ actually endorsed content generated by a user with polarity $P_u$ after being exposed to it. An underlying assumption is that if v follows u then v is exposed to all content from u. The expected decrease in RWC for adding an edge $(u,v)$ is then simply $p(u,v)$ times the decrease in RWC that will be seen if the edge actually is added.

So how do we calculate the polarity $P_u$ of user u? Starting with the vertex for u, we determine the expected number of time steps for a random walk to arrive at a high degree vertex in partition X ( $l_{u}^{X}$ ), and again for partition Y ( $l_{u}^{Y}$ ). Do this for all other users $u'$ as well.

Let $\rho^{X}(u)$ be the fraction of other vertices $u'$ for which $l_{u}^{X} < l_{u'}^{X}$ , and $\rho^{Y}(u)$ be the fraction of other vertices $u'$ for which $l_{u}^{Y} < l_{u'}^{Y}$ .

Now $P_u = \rho^{X}(u) - \rho{Y}(u) \in [-1,1]$ .

We can compute the top-k edges under this model using Fagin’s algorithm: create two ranked lists of edges (u,v), one ranked by decreasing RWC as per the simplified algorithm, and one ranked by decreasing probability of acceptance. “Fagin’s algorithm parses the two lists in parallel to find the edges that optimize the expected decrease E(u,v).”

Instead of having to recompute RWC from scratch each time we want to calculate how much it will decrease when adding an edge, the authors show a way to incrementally compute it – this provides an order of magnitude speed-up in the algorithm runtime.

Case study

In order to provide qualitative evidence on the functioning of our algorithms on real-world datasets, we conduct a case study on three datasets… We can verify that the recommendations we obtain are meaningful and agree with our intuition for the proposed methods…

In the table below, the ROV row represents the recommendations without acceptance probability taken into account, and ROV-AP the recommendations that do consider acceptance probability.

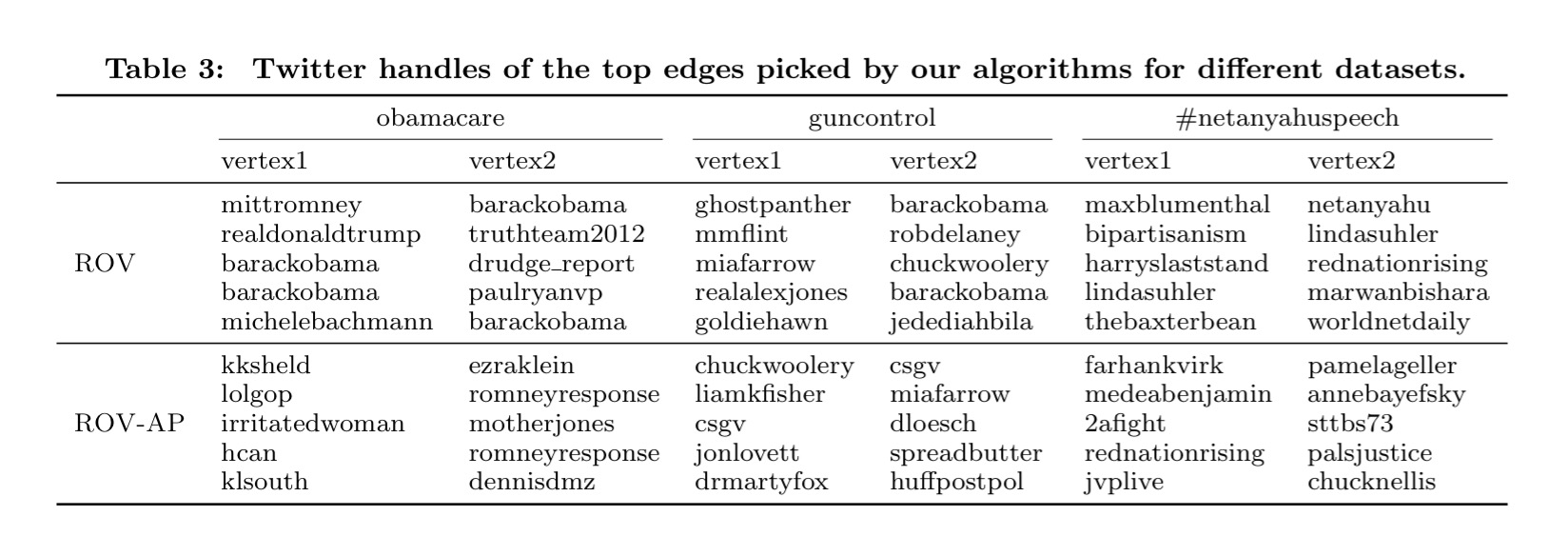
For example, for obamacare ROV recommends edges from mitromney to barackobama, and from barackobama to paulryanvp. Even though these edges indeed connect opposing sides, they might be hard to materialize in the real world. This issue is mitigated by ROV-AP which recommends edges between less popular users, yet connects opposing viewpoints.

Dear Twitter

Dear Twitter,

You have it in your power to truly differentiate your platform and make the world a better place by implementing controversial topic and filter bubble detection (per the paper we looked at yesterday), together with letting users see their polarity score (per today’s paper) and making controversy reducing / filter-busting follower recommendations (also per today’s paper). This would be something new and unique in the world of mass media consumption, and could help to make Twitter great again.

How about it?

Regards, Adrian.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic