The SNOW theorem and latency-optimal read-only transactions Lu et al., OSDI 2016
Consider a read-only workload (as in 100%). You can make that really fast – never any need to coordinate, never any need to invalidate any cached values… Now consider a write-only workload – you can make that even faster, if no-one’s ever going to read the value… ;). What this unrealistic thought-experiment reveals is that there’s clearly a trade-off between reads and writes, and it’s the mixing of the two that causes all of the interesting challenges. In the context of distributed systems (at least two servers, at least three clients), Lu et al. help us to reason about that trade-off when it comes to read-only transactions running in a mixed workload environment. In particular they show that it’s SNOW good trying to build a system that provides the highest levels of guarantees coupled with the lowest possible latency – it’s impossible. (Yes, that’s a terrible pun. You’re welcome). But it is possible to have any three of the four S,N,O,W properties (which I’ll describe next). So that becomes a lens by which you can examine an existing system, and if it provides < 3 of them, there’s a theoretical improvement that could be made.
When examining existing systems we were able to derive latency-optimal read-only transaction algorithms for some, but not all of them. Investigating the cause of this dichotomy led us to discover a trade-off between the latency and the power of read-only transactions. We prove this trade-off is fundamental with the SNOW Theorem, which states it is impossible for a read-only transaction algorithm to provide all four desirable properties: Strict serializability, Non-blocking operations, One response from each shard, and compatibility with conflicting Write transactions.
Which once you put it like that, already starts to feel like a message from the Ministry of the Bleedin’ Obvious (you can’t combine something that requires an absence of coordination, with something that requires coordination…). But the analysis is quite interesting, as is the fact that you can have any three of the four.
S is for Strict Serializability
The ‘S’ in SNOW stands for Strict Serializability. That’s what you get when you combine the gold standard for transaction isolation (serializability) with the gold standard for distributed system consistency (linearizability). It’s as if transactions were processed in real-time order on a single machine.
We’ve looked extensively at consistency and isolation in previous editions of The Morning Paper. Suffice to say, even before introducing distribution, most relational databases used in practice don’t even offer serializability (or if they do, it is never used in practice), and a weaker consistency model called causal consistency is the best we can do if we want to preserve availability. (See also HAT). (And down the rabbit-hole we could go, discussing what availability really means… but let’s not do that here).
What all this means is that Strict Serializability, while giving the best programming model, is also very fertile ground for impossibility results.
N is for Non-blocking
The N in SNOW stands for non-blocking:
We define non-blocking operations to require that each server can handle the operations within a read-only transaction without blocking for any external event. That is, a process never voluntarily relinquishes a processor.
The first thing I think of when I read that, is that clearly all I/O is out. But I don’t think the authors can really quite mean this – surely in response to a read request a server should be allowed to read the requested value from storage if it doesn’t happen to be in memory already? Examples of non-blocking operations that are explicitly forbidden by this model though include waiting on messages from other servers or from clients, waiting for timeouts to fire, or waiting on a lock to become available.
The spirit of the non-blocking requirement is that we are seeking the lowest possible latency for read-only transactions, and anything which blocks is clearly in opposition to this.
O is for One response per read
The O in SNOW combines a (no more than) one round-trip to each server per request requirement with a requirement that each response from a server contains no more than one value for each read.
The one version subproperty aligns with the latency of read-only transactions. If a server sends multiple versions of a value, that much more time is spent serializing, transmitting, and deserializing the values. The one round-trip subproperty strongly aligns with the latency of read-only transactions.
W is for Write transactions
The W in SNOW stands for the ability of a read-only transaction to co-exist with conflicting write transactions.
In this section we find a candidate for understatement of the year!
The ability to coexist with conflicting write transactions is desirable because write transactions make programming application logic much easier.
(a) It is indeed pretty hard to program updates without writes, and…
(b) given that, at least a bare minimum of write transaction support to prevent dirty writes is required if read transactions are to have any real meaning.
If reads and writes can’t co-exist, it doesn’t mean you can’t have writes at all, it just means either reads or writes will have to block while the other proceeds.
SNOW is impossible
I’m going to give you just the briefest version of the proof, see §4.2 for full details.
The intuition of the proof is that when a transaction with writes commits, there is a point at every server when the transaction becomes visible, i.e., newly arriving reads will see its effect. However, the asynchronous nature of the network allows read requests to arrive before the transition on one server, and after the transition on another… Turning this intuition into a proof, however, turns out to be more complex…
SNOW is tight
Not as in SNOW won’t buy a round of drinks at the bar, but as in every combination of three out of the four properties is possible. You can have read-only transaction algorithms that satisfy S+O+W, N+O+W, and S+N+O.
Given that the SNOW Theorem is tight, we define a read-only transaction algorithm to be SNOW-optimal if its properties sit on the boundary of the SNOW Theorem, i.e., it achieves three out of the four SNOW properties. In the four different combinations of SNOW-optimality, S+N+O and N+O+W favor the performance of read-only transactions since non-blocking and one response lead to low latency. We call algorithms that satisfy N+O latency-optimal. In contrast, property combinations S+O+W and S+N+W lean towards the power of read-only transactions as they provide the strongest consistency guarantee and compatibility with conflicting write transactions.
Any algorithm that is not SNOW-optimal has at most two of the properties:
We improve upon such algorithms by keeping the SNOW properties they provide and adding at least one of the latency-related properties. (We do not add strict serializability or compatibility with conflicting write transactions because doing so would change the base system into something new).
On this basis, the authors look at COPS and derive a new COPS-SNOW algorithm that is latency optimal (but not SNOW-optimal), and at Rococo where they derive a SNOW-optimal but not latency-optimal algorithm.
We have found one common insight in our new algorithms that we think will be useful in deriving other SNOW-optimal algorithms. This key insight is to make reads cheaper by making writes more expensive.
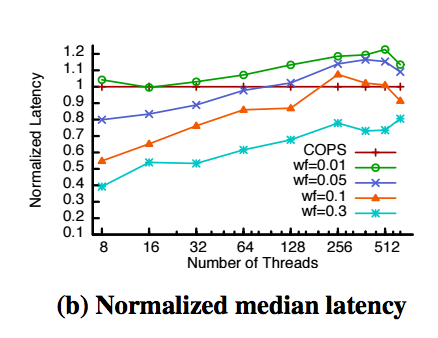
Here’s a chart comparing the median latency of COPS-SNOW to the base COPS algorithm, for varying fractions of writes in the workload. As the write-fraction approaches 0.3, COPS-SNOW’s advantage becomes substantial.
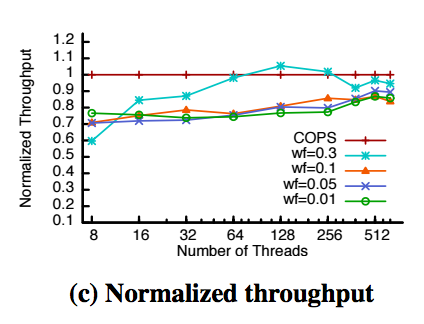
We pay for that with reduced throughput:
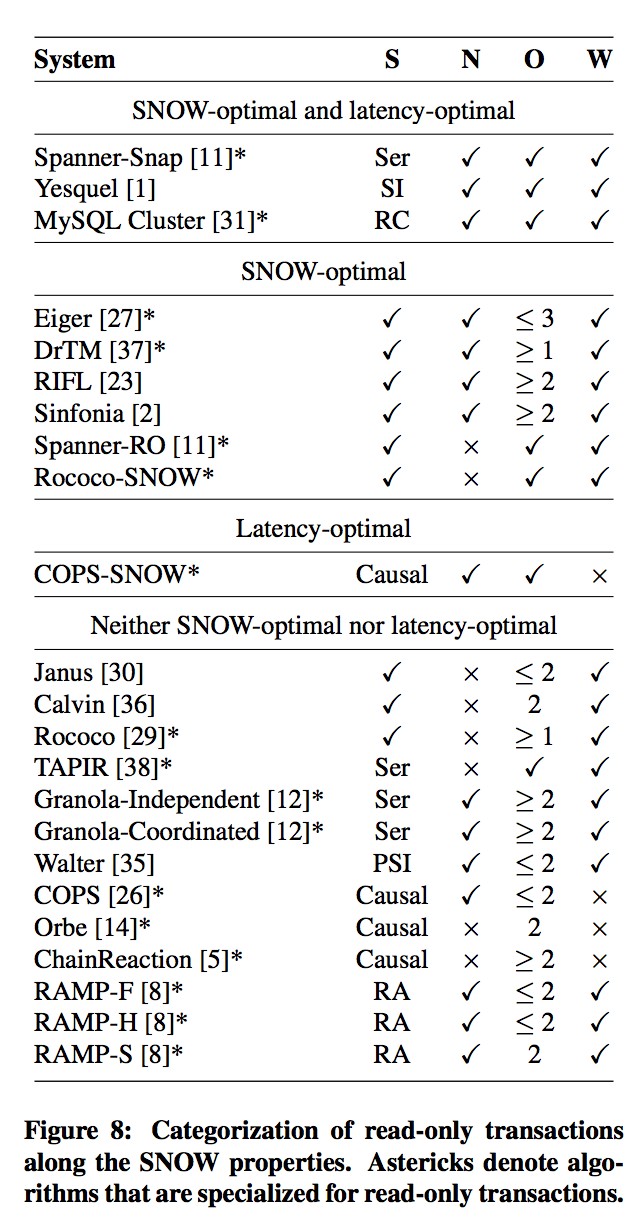
The related work section contains a rather nice table summarising how various existing systems stack up against the SNOW properties:
It also contains the following very academic assertion:
The SNOW theorem… states a property cannot always be satisfied: it is impossible to guarantee a bad thing (violating strict serializability) will never happen. Any system that can violate a safety property is not safe, and thus cannot be used in practice.
While I admire the spirit, we’d pretty much have to turn off every system running in every datacenter everywhere if this were literally true!