ApproxHadoop: Bringing Approximations to MapReduce Frameworks – Goiri et al. 2015

Yesterday we saw how including networking concerns in scheduling decisions can increase throughput for MapReduce jobs (and Storm topologies) by ~30%. Today we look at an even more effective strategy for getting the most out of your Hadoop cluster: doing less work! On one side of the house we have the argument that “having lots of data beats smarter algorithms” (for example, when training a machine learning model), but on the other side of the house “processing less data can get you results faster and cheaper.” In particular, if you’re able to trade a little bit of accuracy, and “process less data” in a disciplined way so that you understand exactly how much accuracy you’re giving up, then you can dramatically reduce the cost of computations. For example, if you can tolerate a 1% error with 95% confidence, then according to the results in this paper you could reduce job execution time by a factor of 32! This is of course the world of probabilistic data structures and approximate computing.

What’s particularly nice about the ApproxHadoop solution is that it’s super easy to apply. Just derive your Mapper, Reducer, and InputFormat classes from the ApproxHadoop provided classes in place of the regular Hadoop ones, specify the target error bound at a confidence level, and you’re good to go. I have a suspicion that a good number of Hadoop jobs would produce perfectly acceptable business results at the 1% error bound, which adds up to a whole lot of savings for not a lot of work!

As a concrete example, Web site operators often want to know the popularity of individual Web pages, which can be computed from the access logs of their Web servers. However, relative popularity is often more important than the exact access counts. Thus, estimated access counts are sufficient if the approximation can significantly reduce processing time.

ApproxHadoop supports three different mechanisms to introduce approximations to Hadoop processing:

• input data sampling, in which only a subset of the input data is processed
• task dropping, in which only a subset of tasks are executed, and
• user-defined approximation in which the user can explicitly provide both a precise and an approximate version of a task’s code.

The paper concerns itself with the first two methods, which are used in combination to achieve the desired accuracy levels. Of course the key thing to understand is the relationship between the amount of sampling and task dropping we do, and the accuracy of the end results. The authors use multi-stage sampling theory and extreme value theory to compute error bounds. Multi-stage sampling is used for jobs that compute aggregations (for example, sum, count, average, ratio), and extreme value theory is used for jobs that compute extremes (e.g. minimum, maximum).

Take the example of computing a sum. If the data is partitioned into N data blocks, we will read from n of them. And if each block has M items, we will process only m of them. The approximate sum will therefore be given by:

(N/n) * (M/m) * the_sum_of_all_values_we_actually_processed

By sampling values from each cluster of data, the inter-cluster and intra-cluster variances can be calculated and these in turn are used to predicted error bound at a given degree of confidence for N, n, M, and m.

For jobs that produce multiple intermediate keys, we view the summation of the values associated with each key as a distinct computation.

Consider the well-trodden word count example. It is possible that the sample from a given data block does not contain entries for a word. The approximate methods work correctly when such a missing element can be assumed to have a zero count. It is also possible that a very infrequently occurring word could be missed across all blocks. Therefore if it is important to find every intermediate key the approach is not suitable. For e.g. a top-k style query this is clearly not a problem.

The extreme value computation (for example, computing the minimum value) relies on the Generalized Extreme Value (GEV) distribution:

In extreme value theory, the Fisher-Tippett-Gnedenko theorem states that the cumulative distribution function (CDF) of the minimum/maximum of n independent, identically distributed (IID) random variables will converge to the Generalized Extreme Value (GEV) distribution as n → ∞, if it converges. The GEV distribution is parameterized by three parameters µ, σ, and ξ, which define location, scale, and shape, respectively. This theorem can be used to estimate the min/max in a practical setting, where a finite set of observations is available. Specifically, given a sample of n values, it is possible to estimate a fitting GEV distribution using the Block Minima/Maxima and Maximum Likelihood Estimation (MLE) methods.

Assuming that the map task produces values for some intermediate key (of which we would like to find the minimum) the first step in approximatation is to drop some of the map tasks so that we end up sampling the data set. Each remaining map task produces its own local minimum value. These minimum values are then fitted to a GEV distribution using Maximum Likelihood Estimation as part of the reduce phase.

The integration of ApproxHadoop with the Hadoop Framework is nice and clean.

First there is support for input sampling:

We implement input data sampling in new classes for input parsing. These classes parse an input data block and return a random sample of the input data items according to a given sampling ratio.

And then for task dropping:

We modified the JobTracker to: (1) execute map tasks in a random order to properly observe the requirements of multi-stage sampling, and (2) be able to kill running maps and discard pending ones when they are to be dropped; dropped maps are marked with a new state so that job completion can be detected despite thesemaps not finishing. We also modified the Reducer classes to detect dropped map tasks and continue without waiting for their results.

Mapper classes are modified to collect the necessary error tracking information and pass it to the reducers. JobTracker collects error estimations from all reducers so that it can track error bounds across the entire job.

To estimate errors and guide the selection of sampling/dropping ratios at runtime, reduce tasks must be able to process the intermediate outputs before all the map tasks have finished. We accomplish this by adding a barrier-less extension to Hadoop that allows reduce tasks to process data as it becomes available.

There are two methods for controlling the degree of approximation: either the user can specify a target error bound and confidence level, or the user can explicitly specify dropping and sampling ratios. The former is obviously more complex to implement!

By default, for a job using multi-stage sampling with a user-specified target error bound, ApproxHadoop executes the first wave of map tasks without sampling. It then uses statistics from this first wave to solve the optimization problem and set the dropping/sampling ratios for the next wave.After the second wave, it selects ratios based on the previous two waves, and so on. The above approach implies that a job with just one wave of map tasks cannot be approximated. However, the user can set parameters to direct ApproxHadoop to run a small number of maps at a specific sampling ratio in a first pilot wave. Statistics from this pilot wave are then used to select dropping/sampling ratios for the next (full) wave of maps. This reduces the amount of precise execution and allows ApproxHadoop to select dropping/sampling ratios even for jobs whose maps would normally complete in just one wave.

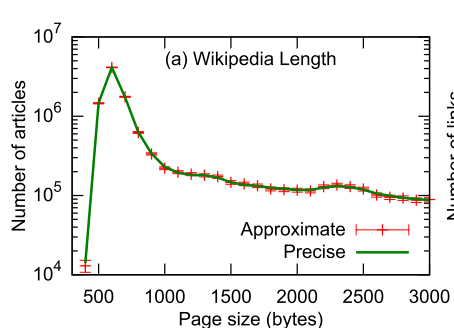
One of the experiments to evaluate the ApproxHadoop framework involved the WikiLength data analysis application whose task is to produce a histogram of the length of wikipedia articles. This was run against the May 2014 Wikipedia data set (9.8GB compressed, 40GB uncompressed) with the 9.8GB split into 161 blocks. Take a look at the graph below which compares the approximated distribution with the precise version. The red error bars show the 95% confidence interval. Do you really need the precise version???

This approximation was produced with an input sampling ration of 1% (i.e. each Map task processes 1 out of every 100 data items)!

The authors also study WikiPageRange, log processing, and an optimization application:

Using extensive experimentation with real systems and applications, we show that ApproxHadoop is widely applicable, and that it can significantly reduce execution time and/or energy consumption when users can tolerate small amounts of inaccuracy. Based on our experience and results, we conclude that our framework and system can make efficient and controlled approximation easily accessible to MapReduce programmers.