Interactive checks for coordination avoidance

Interactive checks for coordination avoidance Whittaker & Hellerstein et al., VLDB’19

I am so pleased to see a database systems paper addressing the concerns of the application developer!

To the developer, a strongly consistent system behaves exactly like a single-threaded system running on a single node, so reasoning about the behaviour of the system is simple¹. Unfortunately strong consistency is at odds with performance… On the other hand weak consistency models… put a tremendous burden on the application designer to reason about the complex interleavings of operations that are allowed by these weak consistency models.

To be able to reason effectively about a system, it’s tremendously helpful to be able to rely on some things that we know will always be true. The fancy word for those is invariants, because whatever happens they never vary. A example class of application invariants is database integrity constraints. Unfortunately, under weak consistency models finding solid ground to reason about invariants is really hard:

Even if every transaction executing in a weakly consistent system individually maintains an application invariant, the system as a whole can produce invariant-violating states.

In a distributed setting with weak consistency, an object is replicated across a set of servers. Transactions occur at those replicas, which may update the local state of the object. The system periodically merges the state at replicas to prevent the system state from diverging. The fancy word for two (or more) things joining or coming together is confluence. That brings us to invariant confluence. An invariant confluent object maintains its invariants during merge operations. So if we had one of these very special objects, and we knew that every transaction preserved its invariants, and every possible merge preserved its invariants, then we’d be able to reason with some sanity again. Moreover, the system can have higher performance because it doesn’t need to coordinate:

Bailis et al. introduced the notion of invariant confluence as a necessary and sufficient condition for when invariants can be maintained over replicated data without the need for any coordination.

See Coordination avoidance in database systems for more details. That paper was published back in 2014 and showed some tremendous performance benefits, so why aren’t we all programming with invariant confluent objects already??

Unfortunately, to date, the task of identifying whether or not an object is actually invariant confluent has remained an exercise in human proof generation… Hand-written proofs of this sort are unreasonable to expect from programmers. Ideally we would have a general-purpose program that can automatically determine invariant confluence for us.

The first part of this paper addresses the challenge of making invariant confluence machine checkable. This isn’t possible in the general case, but we can design a decision procedure that works in the common case.

The second part of the paper extends the performance and reasoning benefits of invariant confluence to more objects: the idea here is that even if an object isn’t invariant confluent as a whole, we might be able to partition its state into segments that are invariant confluent within an individual segment. Then so long as we stay within a segment we can operate without coordination, but we’ll still have to coordinate when crossing segments.

A decision procedure for invariant confluence

My ideal developer experience here would be that I make a pull request for an application, and an invariant confluence checker runs against the code and gives me either the all clear or a concise example showing why the change breaks invariant confluence. We’re not there yet! In fact, the bulk of the paper addresses the underlying theory that makes a decision process possible, and we only get a small hint of what the developer experience might be like in the evaluation.

Consider an example in which the state of an object consists of a pair of integers $(x,y)$ and the merge operation for two pairs $(x_1, y_1), (x_2, y_2)$ is defined as $(max(x_1, x_2), max(y_1, y_2))$ . We’d like to maintain an invariant that the product of $x$ and $y$ is zero or less at all times: $xy \leq 0$ .

In the Lucy prototype, the object, its transactions, and the invariant are described in Python like this:

How is that check() method implemented behind the scenes though?

Invariant closure

Deciding invariant confluence in general is hard, but there’s a subset for which it’s a bit easier. Under invariant closure we have the property that merge operations preserve invariants. I.e., given any two invariant satisfying states, the result of their merge is also guaranteed to satisfy the invariant. Invariant closure is simpler to reason about than invariant confluence, and it’s a sufficient condition to establish invariant confluence, so this is the approach taken by existing systems.

Unfortunately, invariant closure is not necessary for invariant confluence, so if an object is not invariant closed, these systems cannot conclude that the object is not invariant confluent.

We’d like to widen the set of objects that we can confidently claim are invariant confluent, and to do that we need to step beyond the bounds of invariant closure.

Reachability

Invariant closure is a universally quantified proposition. I.e., it says for all invariant preserving states $S_1$ and $S_2$ their merge will be invariant preserving. Going back to the pair-of-integers example and the invariant that their product be less than or equal to zero, there are clearly cases where this doesn’t hold, e.g. merging the valid states (-1,1) and (1, -1) results in the invalid (1,1).

But what if the states that would cause invariant closure to fail aren’t actually reachable? We don’t really need that unqualified ‘for all’. Instead we can replace it with ‘for all reachable invariant preserving states…’.

The decision procedure

Incorporating the idea of reachability, the decision process for invariant confluence looks like this:

A user provides Algorithm 1 with an object $O = (S,\sqcup)$ , a start state $s_0$ , a set of transactions $T$ , and an invariant $I$ . The user then interacts with Algorithm 1 to iteratively eliminate unreachable states from the invariant. Meanwhile, the algorithm leverages an invariant closure decision procedure to either (a) conclude that $O$ is or is not $(s_0,T,I)$ -confluent or (b) provide counterexamples to the user to help them eliminate unreachable states. After all unreachable states have been eliminated from the invariant, Theorem 2 allows us to reduce the problem of invariant conﬂuence directly to the problem of invariant closure, and the algorithm terminates.

Section 5 in the paper discusses an additional check for invariant confluence that be undertaken without any user interaction and also covers some cases outside of invariant closure. It relies on the idea of merge reducibility: an object is merge reducible if for every possible state you can reach via merges, you could also reach that state without merges just through a sequence of transactions. Merge reducibility is a sufficient condition for invariant confluence, but is hard to automatically determine. For a subset of merge reducible objects (join-semilattices) we can though.

Segmented invariant confluence

I’m out of space to do justice to segmented invariant confluence, so I’m going to refer you to §6 in the paper for the details. The essence of the idea is easy to grasp though, if an object as a whole isn’t invariant confluent, maybe we can sub-divide it into parts that are:

The main idea behind segmented invariant confluence is to segment the state space into a number of segments and restrict the set of allowable transactions within each segment in such a way that the object is invariant confluent within each segment (even though it may not be globally invariant confluent). Then, servers can run coordination-free within a segment and need only coordinate when transitioning from one segment to another.

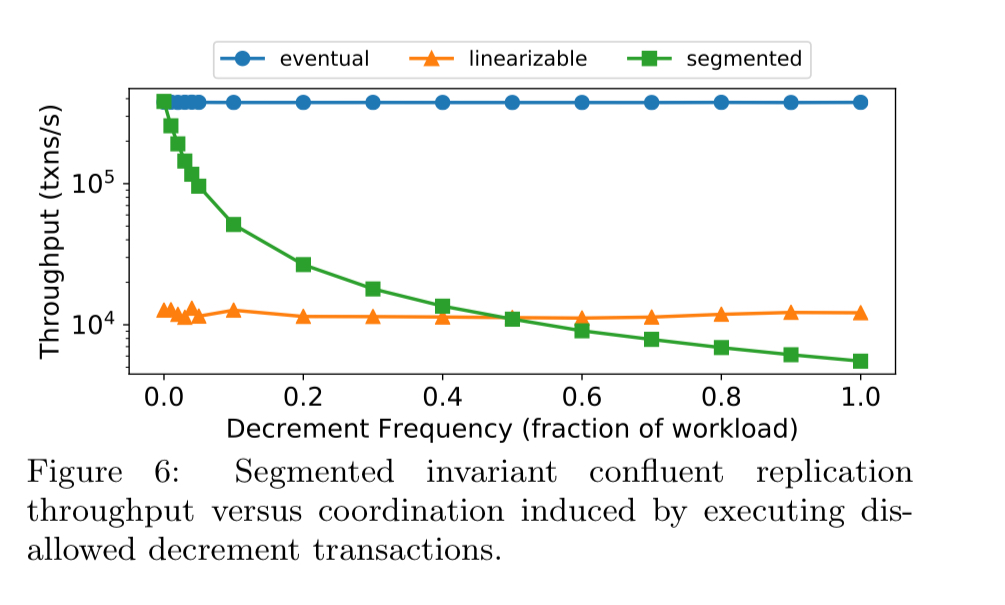
The evaluation shows that when you only infrequently need to coordinate across segments, segmented invariant confluence can sustain 10-100x more throughput than linearizable replication. If you have to cross segments too often though, linearizable replication still wins.

So now life is easy, right?

We’re going in the right direction with making higher performing systems that are easier for developers to reason about, but there’s still work to be done.

The decision algorithm requires input from the application developer to determine the set of unreachable states. Determining if a state is unreachable is easier than determining invariant confluence, but it’s still not easy: “Unlike with reachable states— where verifying that a state is reachable only requires thinking of a single way to reach the state— verifying that a state is unreachable requires a programmer to reason about a large number of system executions and conclude that none of them can lead to the state.” Automating more of this process is future work.
For segmented invariant confluence, it’s the responsibility of the application developer to come up with a segmentation that works. “This can be an onerous process.” Automatically suggesting segmentations is future work.

Maybe in theory, but in practice plenty of developers struggle with the correct use of transactions! ↩

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic