Challenging common assumptions in the unsupervised learning of disentangled representations Locatello et al., ICML’19

Today’s paper choice won a best paper award at ICML’19. The ‘common assumptions’ that the paper challenges seem to be: “unsupervised learning of disentangled representations is possible, and useful!”

The key idea behind the unsupervised learning of disentangled representations is that real-world data is generated by a few explanatory factors of variation which can be recovered by unsupervised learning algorithms. In this paper, we provide a sober look at recent progress in the field and challenge some common assumptions.

What exactly is a ‘disentangled representation’ and why might we want one?

Put the ‘disentangled’ part to one side for a moment, and let’s start out by revisiting what we mean by a representation. Given a real-world observation (e.g. of an image or video), a representation is a transformation of (typically to a lower dimensional space in order to be useful) that somehow preserves the salient information in the so that we can still use to extract useful information about the input (e.g. for building classifiers). As a trivial example, suppose we had real world observations consisting of 1000 points sampled from a straight line, a good lower-valued representation would be a (gradient, intercept) tuple. Of course real-world examples are much more complex than this!

A disentangled representation is a representation with a compact and interpretable structure, which captures the essence of the input independent of the task the representation is ultimately going to be used for. That’s quite tricky – even in my contrived straight line example what looked to be a great representation would be useless if the task turned out to be calculating the area of the the rectangle enclosed by the points in the observation.

While there is no single formalized notion of disentanglement (yet) which is widely accepted, the key intuition is that a disentangled representation should separate the distinct information factors of variation in the data. A change in a single underlying factor of variation should lead to a change in a single factor in the learned representation.

The state of the art for representation learning centres around Variational Autoencoders, using one deep neural network to learn a representation, and another one to attempt to reconstruct the original input from that representation. The representation is usually taken as the mean of the approximate posterior distribution of the first (encoding) network.

In theory, disentanglement is impossible

We theoretically prove that (perhaps unsurprisingly) the unsupervised learning of disentangled representations is fundamentally impossible without inductive biases both on the considered learning approaches and the data sets.

The full proof is giving in appendix A (missing from my copy of the pdf), but it boils down to this:

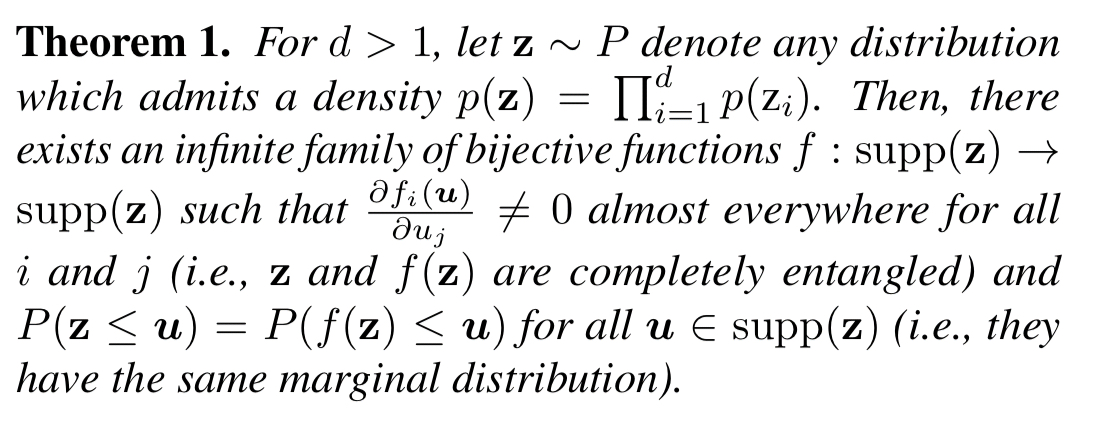
My layman’s interpretation is this: given all the possible ways we could decompose the input into factors, whatever representation we ultimately choose there is some other representation in which a change to a single dimension in the first impacts all the dimensions of the second (they are entangled). There’s no way for an unsupervised method to distinguish between these two equivalent generative models, and thus the resulting learned representation must be entangled with at least one of them.

After observing , we can construct many generative models which have the same marginal distribution of . Any one of these models could be the true causal generative model for the data, and the right model cannot be identified given only the distribution of .

For a wonderful demonstration of this in lower dimensions, see ‘Same stats, different graphs’.

In practice, might we be able to learn disentangled representations anyway?

While Theorem 1 shows that unsupervised disentanglement learning is fundamentally impossible for arbitrary generative models, this does not necessarily mean that it is an impossible endeavour in practice. After all, real world generative models may have a certain structure that could be exploited through suitably chosen inductive biases.

But, the authors argue, you should make explicit the inductive biases you are selecting.

To investigate all this the authors take six recent unsupervised disentanglement methods, train them over seven different data sets, and evaluate them using six different disentanglement measures. The result is a corpus of more than 10,000 trained models. The library used to train and evaluate these models, disentanglement_lib has been made available at https://github.com/google-research/disentanglement_lib. After training, each model is evaluated by taking 50 different random seeds and then evaluating the representation for each seed using the considered metrics.

To fairly evaluate the different approaches, we separate the effect of regularization (in the form of model choice and regularization strength) from the other inductive biases (e.g., the choice of the neural architecture). Each method uses the same convolutional architecture, optimizer, hyperparameters of the optimizer and batch size. All methods use a Gaussian encoder where the mean and the log variance of each latent factor is parametrized by the deep neural network, a Bernoulli decoder and latent dimension fixed to 10.

Key results

Nice posterior, shame about the mean…

Most of the considered methods use the mean vector of the Gaussian encoder as the representation, rather than a sample. The mean representation turns out to be mostly correlated with regularization strength (i.e., a hyperparameter, not a latent variable in the input)!

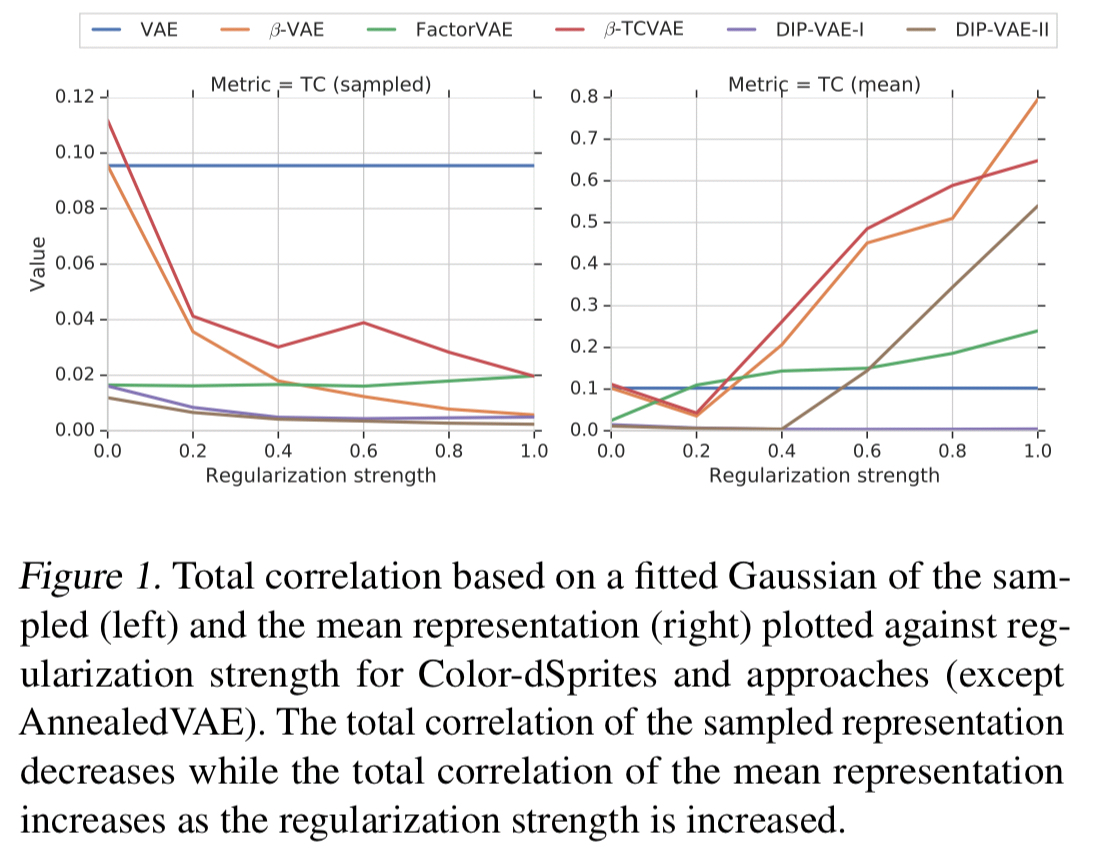
… these results lead us to conclude with minor exceptions that the considered methods are effective at enforcing an aggregated posterior whose individual dimensions are not correlated but that this does not seem to imply that the dimensions of the mean representation (usually used for representation) are uncorrelated.

Disentanglement metrics mostly agree

The six disentanglement metrics mostly agree with other (are correlated), with the exception of the Modularity measure, so at least directionally it doesn’t seem to matter too much which one you pick. The degree of correlation changes between different data sets.

Luck and tuning

… the choice of hyperparameters and the random seed seems to be substantially more important than the choice of the objective function.

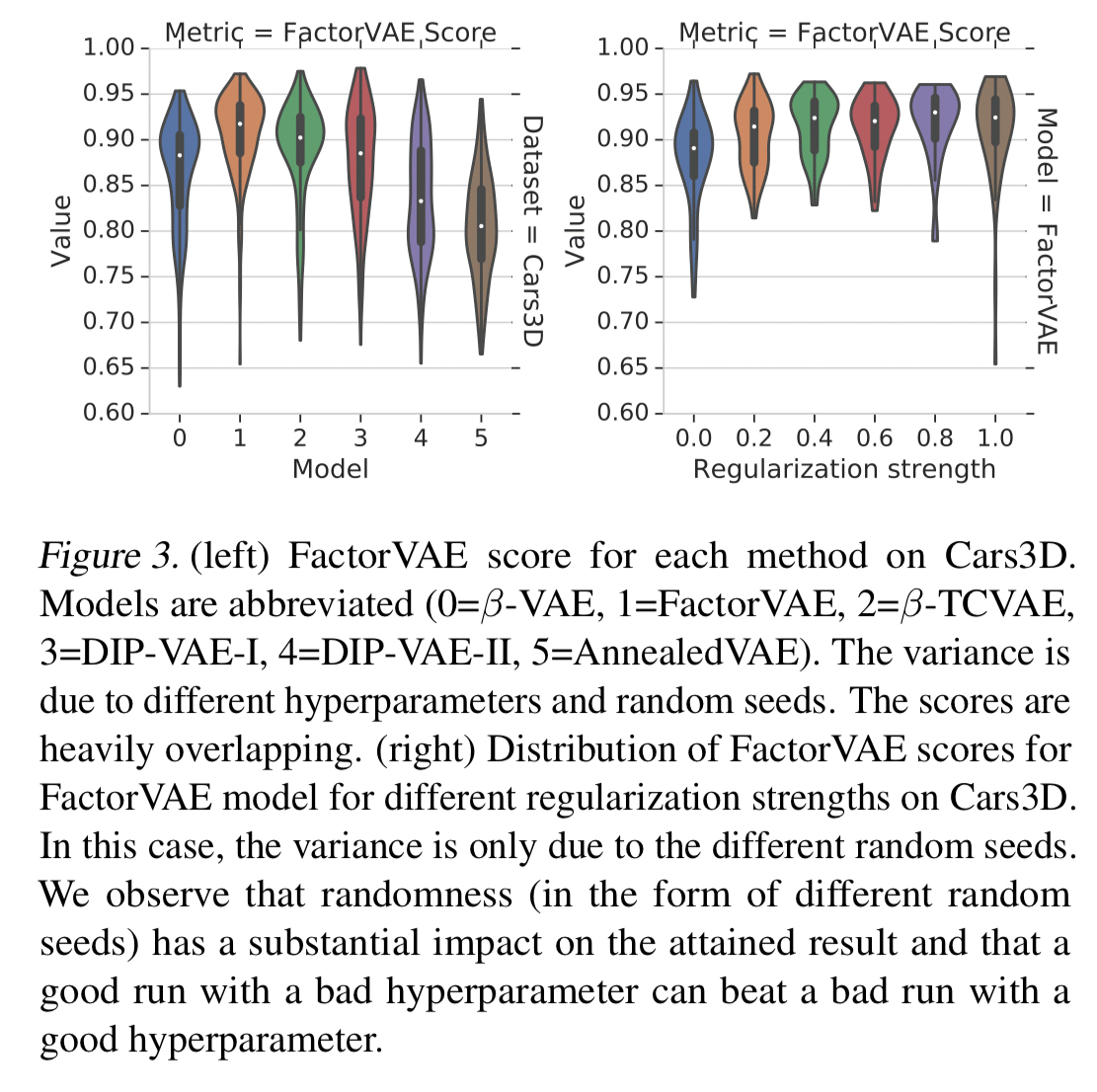
A bad run (unlucky choice of seed) with a good hyperparameter can perform worse than a lucky choice of seed with a bad hyperparameter. It seems that disentanglement scores are heavily influenced by the randomness of seed selection and the strength of regularisation (controlled by a hyperparameter).

There doesn’t seem to be a general purpose way of choosing models and hyperparameters

Looking at the performance of different regularisation strengths across models and data sets we find no conclusive correlation:

Overall, there seems to be no model consistently dominating all the others, and for each model there does not seem to be a consistent strategy in choosing the regularization strength to maximize disentanglement scores.

No clear pattern emerges when attempting to select hyperparameters based on other measures such as the reconstruction error either.

Transfer works, kind of

If we have found good hyperparameter settings on one data set, can we transfer them to another data set? Between the dSprites and Color-dSprites datasets this strategy worked well, but performance is still dominated by choice of the random seed. With other model pairs it did not work as well.

• With the same metric and same data set (but a different random seed), we match we match or outperform the original selection (seed) 81% of the time.
• If we hold the metric constant but transfer settings across datasets we match or outperform a random selection 59% of the time.
• If we transfer across both metrics and datasets we do only a little better than chance: matching or outperforming a random selection only 55% of the time.

Unsupervised model selection remains an unsolved problem. Transfer of good hyperparameters between metrics and data sets does not seem to work as there appears to be no unsupervised way to distinguish between good and bad random seeds on the target task.

The disentangled representations might not be all that useful anyway

The question here is “do representations that score higher on disentanglement metrics yield better performance when used in downstream learning tasks?” The authors chose as a representative task recovering the true factors of variations from the learned representations, using either multi-class logistic regression, or gradient boosted trees.

There’s some correlation for all metrics apart from Modularity on two of that data sets, dSprites and Shapes3D, but not for the others. Results with other models may be different, however, as far as this paper is concerned:

…the lack of concrete examples of useful disentangled representation necessitates that future work on disentanglement methods should make this point more explicit.

Implications

The authors conclude with three recommendations:

• Future works on disentanglement representations should make explicit the roles of inductive biases and supervision.
• We need to look further into the usefulness of disentangled representations. Maybe they perform better on other criteria such as interpretability and fairness?
• It’s easy to draw spurious conclusions from experimental results if you only consider a subset of methods, metrics, and data sets: future work should perform experiments on a wide variety of data sets to see whether conclusions and insights are generally applicable. The disentanglement library released by the authors can help with this.

I hope it turns out that disentangled representations do prove to be better by some measures. That would tell us that we really are able to extract some seemingly genuine latent variables that are meaningful in the input space. But perhaps some input domains just don’t have any natural disentangled latent features? At least we do know that we can learn lower dimensional representations that are useful, even if they are imperfect and/or somewhat arbitrary!