Data Shapley: equitable valuation of data for machine learning Ghorbani & Zou et al., ICML’19

It’s incredibly difficult from afar to make sense of the almost 800 papers published at ICML this year! In practical terms I was reduced to looking at papers highlighted by others (e.g. via best paper awards), and scanning the list of paper titles looking for potentially interesting topics. For the next few days we’ll be looking at some of the papers that caught my eye during this process.

The now somewhat tired phrase “data is the new oil” (something we can consume in great quantities to eventually destroy the world as we know it???) suggests that data has value. But pinning down that value can be tricky – how much is a given data point worth, and what framework can we use for thinking about that question?

As data becomes the fuel driving technological and economic growth, a fundamental challenge is how to quantify the value of data in algorithmic predictions and decisions…. In this work we develop a principled framework to address data valuation in the context of supervised machine learning.

One of the nice outcomes is that once you’ve understood what data has high value and what data has low value, you can use this insight to guide future data collection activities and improve your ROI on data gathering. It also turns out that examining data points with low values turns out to be a good way of discovering noisy and/or mislabelled data points. Removing these can improve your model’s performance.

It’s most important to remember at all times when considering this work that we’re talking about the value of data in the context of training a specific model. We can’t give an objective valuation of a data point outside of that context, and a data point that is low value for one task may be high value for another.

… we do not define a universal value for data. Instead, the value of each datum depend on the learning algorithm and the performance metric, as well as on other data in the training set. This dependency is reasonable and desirable in machine learning.

How to judge the value of a data point

Assume we have some fixed training set , a learning algorithm , and a performance score function , where , which takes as input a predictor trained on and returns a performance score.

Let (sometimes written just as ) be a function that quantifies the value of the i-th datum. For an equitable data valuation function we want the following three properties to hold:

1. If a datapoint does not change the performance when it’s added to any subset of the training data, then it should be given zero value.
2. If two different data points, when individually added to any subset of the training data always produce exactly the same change in the predictor’s score, then they should be given the same value by symmetry.
3. When the overall prediction score is the sum of K separate predictions, the value of a datum should be the sum of its value for each prediction.

These three conditions mirror the fairness conditions from cooperative game-theory as defined by Shapley (in 1953), and constrain to have the following form:

In game theory this is called the Shapley value, so here the authors call it the data Shapley value.

Let’s unpick that equation a little:

• Take all possible subsets from that do not include , the data point we wish to value
• For each of these subsets, compute the incremental value that arises when is added back in
• Sum all of those value increments, and divide by the number of subsets to yield the average value increment for a subset of the training data when data point is added to it.

Eqn. 1 could be interpreted as a weighted sum of all possible “marginal contributions” of , where the weight is inverse the number of subsets of size in . This formulation is close to that of leave-one-out where instead of considering the last marginal contribution , we consider each point’s marginal contribution assuming that instead of the whole training set, a random subset of it is given.

The constant is an arbitrary scaling constant and doesn’t affect any of the analysis.

How to make it tractable

You might have spotted the challenge in computing a data Shapley value: it requires us to train and score a model (expensive) for every possible subset of the training data (exponentially many). And then of course we’d like to do this for all of the points in our data set (typically large). So that’s not going to work then.

All is not lost. The authors introduce techniques for approximating data Shapley, tackling each of the three dimensions:

• We can deal with the problem of exponentially many subsets by using Monte Carlo sampling: “in practice, we generate Monte Carlo estimates until the average has empirically converged.”
• We can use early stopping (truncation) when calculating a data Shapley value for a sampled permutation . Whenever is within the performance tolerance (inherent noise) of the marginal contribution is set to zero for the rest of the data points in the permutation.

  Putting these first two optimisations together gives Truncated Monte Carlo Shapley, TMC-Shapley.

• We can reduce the cost of training a model, where that model is trained using a variation of stochastic variant descent, but training the model for one epoch (one pass through the training data) only. This variant is called Gradient Shapley.
• We can reduce the number of data points we have to compute the data Shapley value for by instead computing the value for groups of points. “For example, in a heart disease prediction setting, we could group the patients into discrete bins based on age, gender, ethnicity and other features, and then quantify the data Shapley of each bin.“

Data Shapley in action

There are some really interesting results in the evaluation section, that demonstrate the power of understanding the value of your data points (as well as the efficacy of data Shapley in helping you to do that).

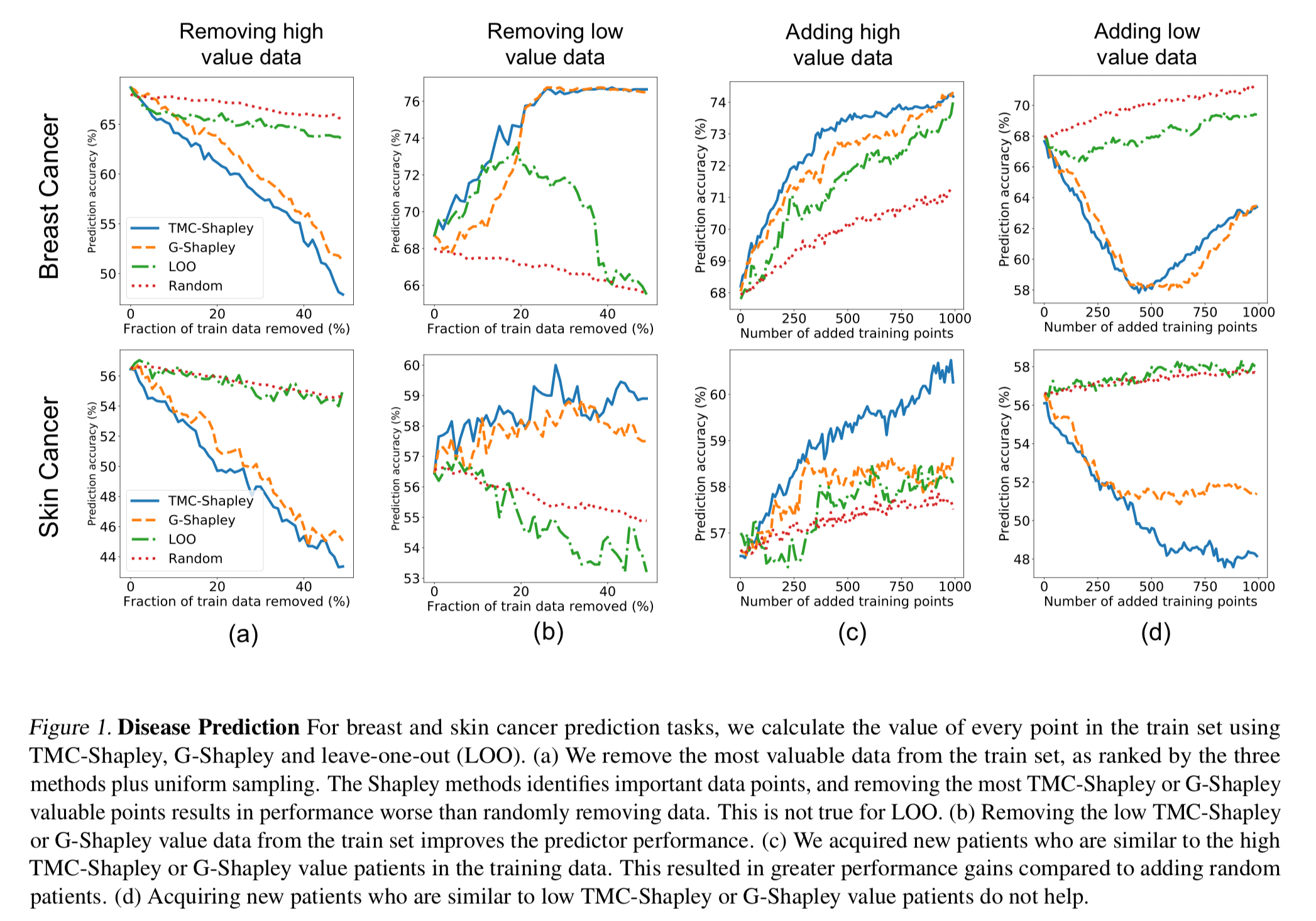
Using the UK Biobank data set and a model for predicting breast and skin cancer, the authors calculated data values for 1000 data points in a training set. Now, if you take data points away from the training set, starting with the most valuable data points, and retrain the model, you can see that model performance drops (Fig 1a).

(Enlarge)

… points that data Shapley considers valuable are crucially important for the model performance while leave-one-out valuation is only slightly better than random valuation (i.e., removing random points).

If you go in the other direction, and start by removing the lowest valued data points, the model performance improves! Points with a low Shapley value harm the model’s performance and removing them improves accuracy (Fig 1b above).

If we wanted to collect more data to improve, then adding data points similar to high value data points (assuming that’s something we can control in data gathering) leads to much better performance improvements than adding low value data points (Fig 1c and d above).

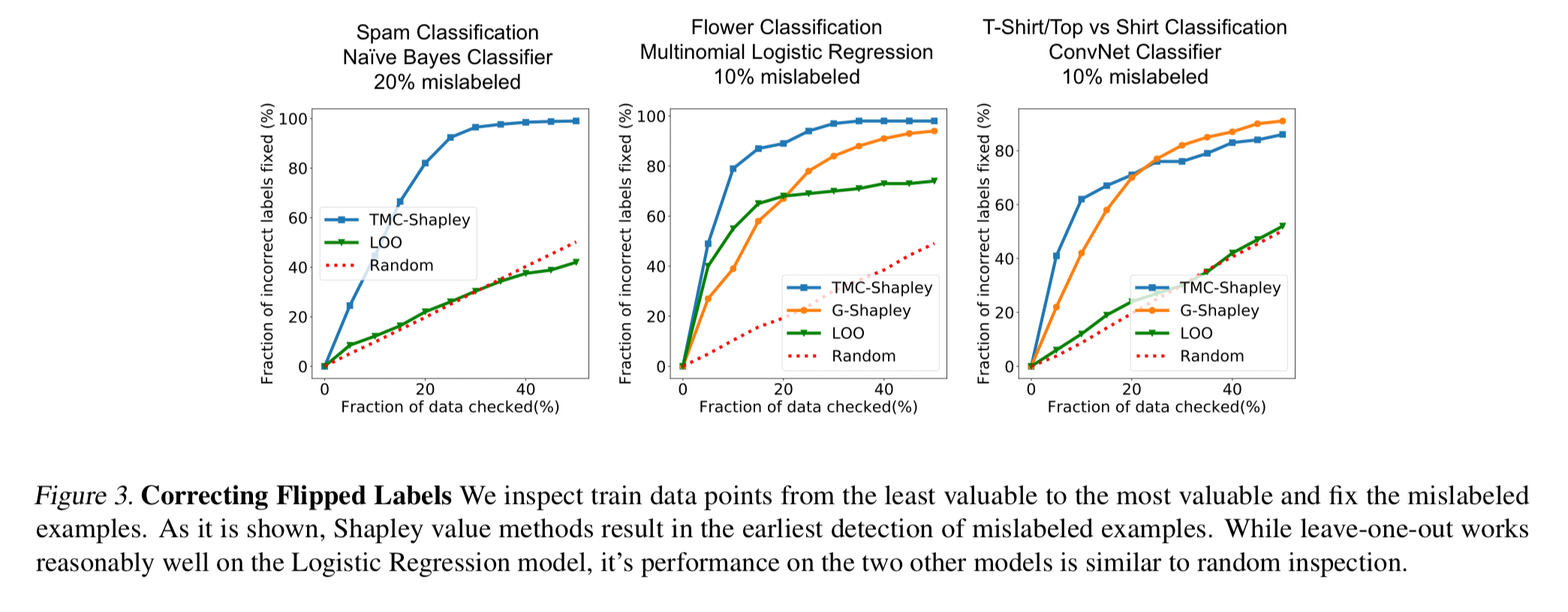
Another experiment trained data with noisy (incorrect) labels and found that the erroneous data points ended up with low data values. Thus by inspecting data points from least valuable to most valuable it’s likely that you will find and be able to correct mislabeled examples.

(Enlarge)

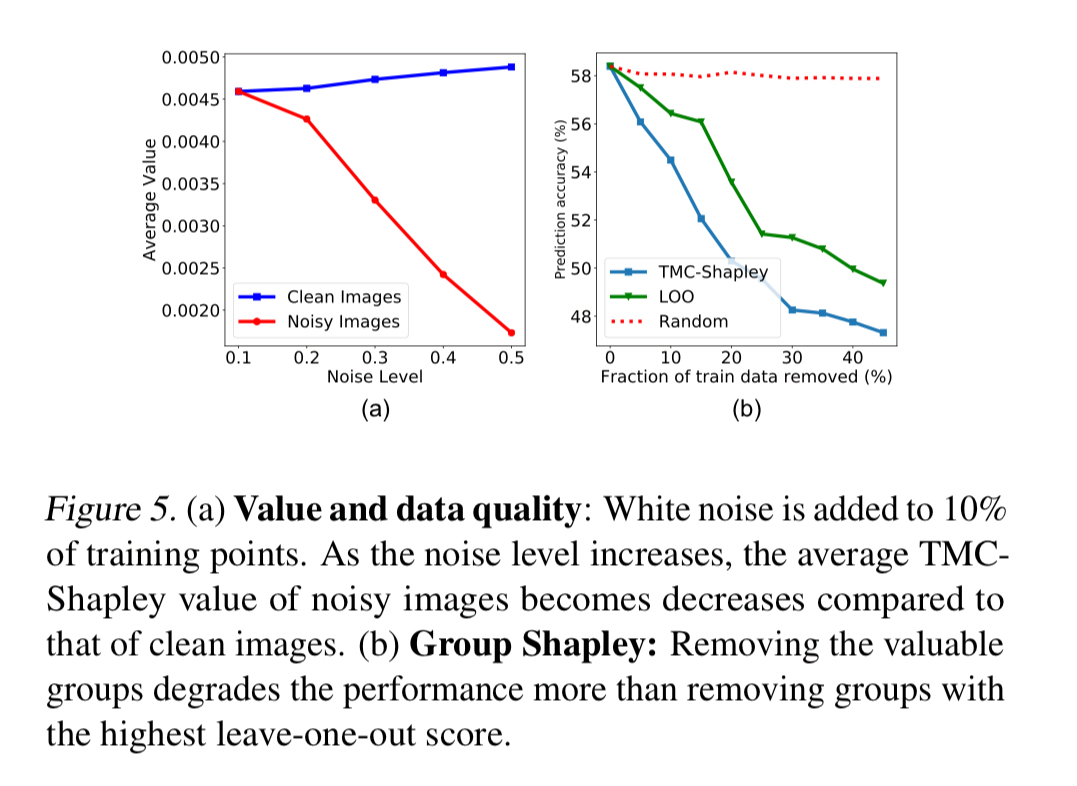
Deliberately adding noise to images reduces data values:

The last word

Data Shapley uniquely satisfies three natural properties of equitable data valuation. There are ML settings where these properties may not be desirable and perhaps other properties need to be added. It is a very important direction of future work to clearly understand these different scenarios and study the appropriate notions of data value. Drawing on the connections from economics, we believe the three properties we listed is a reasonable starting point.

And an important reminder: “… we have skipped over many important considerations about the intrinsic value of personal data, and we focused on valuation in the very specific context of a training set for supervised learning algorithms. “