Learning representations by back-propagating errors

~ Adrian Colyer

Learning representations by back-propagating errors Rumelhart et al., Nature, 1986

It’s another selection from Martonosi’s 2015 Princeton course on “Great moments in computing” today: Rumelhart’s classic 1986 paper on back-propagation. (Geoff Hinton is also listed among the authors). You’ve almost certainly come across back-propagation before of course, but there’s still a lot of pleasure to be had from reading the paper and seeing again with fresh eyes the birth of the idea. Plus, we get the opportunity to take things nice and slow!

We want to build self-organising neural networks that can develop an internal structure appropriate for a particular task domain. Tasks are specified by giving the desired state vector of the output units for each state vector of the input units.

If the input units are directly connected to the output units it is relatively easy to find learning rules that iteratively adjust the relative strengths of the connections so as to progressively reduce the difference between the actual and desired output vectors. Learning becomes more difficult when we introduce hidden units whose actual or desired states are not specified by the task…

Back-propagation is a breakthrough (c. 1986!) algorithm that allows us to build and train neural networks with hidden layers. The learning procedure decides under what circumstances the hidden units should be active in order to achieve the desired input-output behaviour. “This amounts to deciding what these units should represent”. I.e., the hidden units are going to learn to represent some features of the input domain.

Consider networks with a layer on input units at the bottom, any number of intermediate (hidden) layers, and a layer of output units at the top. Connections within a layer, or from higher to lower layers are forbidden. Connections can skip intermediate layers though. (Skip connections would go on to be important components in the training of deep neural networks).

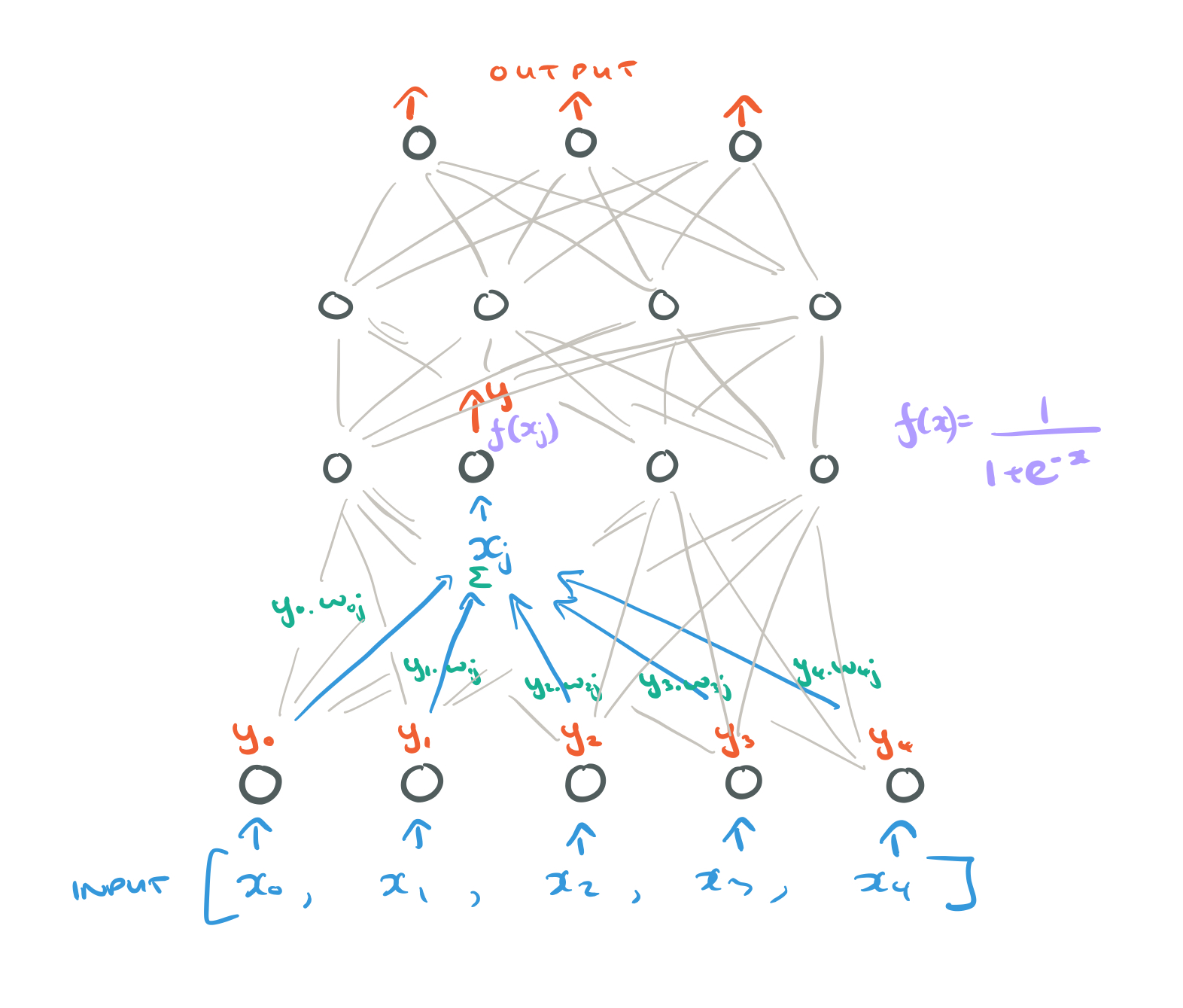
Feeding forward

Consider a unit j, with an input x_j. If the unit is in the input layer, the value x_j is provided by the input vector. But if the unit is in a higher layer, then its input will be a weighted sum of the outputs of all of the lower layer units that feed into it. For each such unit i that feeds into j, we have an output of that unit, y_i, adjusted by a weight on the link between i and j, w_{ij}. So:

[EQN 1] \displaystyle x_j = \sum_{i} y_{i} w_{ij}

We’ll assume that each unit is given an extra input which always has the value of 1. The weight on this extra input is the ‘bias’. (The bias lets us control the value of b in y = ax + b).

We now know how to calculate the input to unit j, but what should j output? The output should be some function of the input, which we call the activation function. The chosen activation function in the paper is the sigmoid function:

[EQN 2] \displaystyle y_j = \frac{1}{1 + e^{-x_j}}

This produces real-valued output, and is differentiable.

By repeating this procedure, starting with the input layer, we can feed-forward through the network layers and arrive at a set of outputs for the output layer.

Patching things up

We can now compare the calculated outputs to the desired output vector.

The aim is to find a set of weights that ensure that for each input vector the output vector produced by the network is the same as (or sufficiently close to) the desired output vector.

For a given input-output case, the error is given by:

[EQN 3] \displaystyle E = \frac{1}{2}\sum_{j}(y_j - d_j)^2

Where y_j is the computed output value of unit j in the output layer, and d_j is its desired state. We can get the total error across all training cases by simple summation of the individual case errors.

(Squaring things is handy when we sum, because it makes all differences positive so that positive and negative differences don’t cancel each other out).

We’d like to make the total error as small as possible (minimise it). To do that, we need to adjust the weights (the only parameters we have available to play with). But how should we adjust them to achieve our goal?

To minimize E by gradient descent it is necessary to compute the partial derivative of E with respect to each weight in the network.

We’d like to know how the error changes as we change the weights, \frac{\partial E}{\partial w}. We don’t know that straight away, but we do know how the error changes as we change the outputs y_j (\frac{\partial E}{\partial y_j}) as E and y are directly related in the equation for E (EQN 3).

\displaystyle \frac{\partial E}{\partial y_j} \frac{1}{2}\sum_{j}(y_j - d_j)^2 = y_j - d_j

So now we know how the error changes in relation to the outputs y. Recall that y_j itself is a function of the input x_j to unit j (EQN 2). So we can also work out how y changes as x changes, \frac{\partial y_j}{\partial x_j}.

If we denote the sigmoid function by \sigma then we have y_j = \sigma(x_j), and the derivative is:

\displaystyle \frac{\partial y_j}{\partial x_j} = \sigma(x_j)\cdot (1 - \sigma(x_j))

Getting closer! We know how the error changes with the output y, and we know how y changes with its input x. Now remember that x_j is itself a function of the weights w_{ij} and the outputs from lower layers which will be multiplied by those weights (EQN 1). So we can work out how x_j changes as we change the weights: \frac{\partial x_j}{\partial w_{ij}}. For a given weight w_{ij} from unit i to unit j the derivative is:
\displaystyle \frac{\partial x_j}{\partial w_{ij}} = y_i

Let’s put all those pieces together in a chain. If we know how the error changes with the output y, and how y changes with the input x, and how x changes with the weight w, then we can chain them together to figure out how the error changes with the the weights. Which is what we wanted to know in order to be able to adjust our weights using gradient descent. This is of course the chain rule from differentiation:
\displaystyle \frac{\partial E}{\partial w} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial x} \cdot \frac{\partial x}{\partial w}

Almost there!

With \frac{\partial E}{\partial w} in hand, the simplest form of gradient descent would be to change each weight by an amount proportional to the accumulated gradient:
\displaystyle \Delta w = - \epsilon \frac{\partial E}{\partial w}

This method does not converge as rapidly as methods which make use of the second derivatives, but it is much simpler and can be easily implemented by local computations in parallel hardware. It can be significantly improved, without sacrificing the simplicity and locality, by using an acceleration method in which the current gradient is used to modify the velocity of the point point weight space instead of its position:

\displaystyle \Delta w(t) = - \epsilon \frac{\partial E}{\partial w}(t) + \alpha \Delta w(t-1)

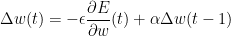
Where t is incremented by 1 for each sweep through the whole set of input-output cases, and \alpha is an exponential decay factor between 0 and 1 that determines the relative contribution of the current gradient and earlier gradients to the weight change.

Variants on the learning procedure have been discovered independently by David Parker (personal communication) and Yann Le Cun.