On the information bottleneck theory of deep learning Anonymous et al., ICLR’18 submission
Last week we looked at the Information bottleneck theory of deep learning paper from Schwartz-Viz & Tishby (Part I,Part II). I really enjoyed that paper and the different light it shed on what’s happening inside deep neural networks. Sathiya Keerthi got in touch with me to share today’s paper, a blind submission to ICLR’18, in which the authors conduct a critical analysis of some of the information bottleneck theory findings. It’s an important update pointing out some of the limitations of the approach. Sathiya gave a recent talk summarising results on understanding optimisation and generalisation, ‘Interplay between Optimization and Generalization in DNNs,’ which is well worth checking out if this topic interests you. Definitely some more papers there that are going on my backlog to help increase my own understanding!
Let’s get back to today’s paper! The authors start out by reproducing the information plane dynamics from the Schwartz-Viz & Tishby paper, and then go on to conduct further experiments: replacing the tanh activation with ReLU to see what impact that has; exploring the link between generalisation and compression; investigating whether the randomness is important to compression during training; and studying the extent to which task-irrelevant information is also compressed.
The short version of their findings is that the results reported by Schwartz-Viz and Tishby don’t seem to generalise well to other network architectures: the two phases seen during training depend on the choice of activation function; there is no evidence of a causal connection between compression and generalisation; and that when compression does occur, it is not necessarily dependent on randomness from SGD.
Our results highlight the importance of noise assumptions in applying information theoretic analyses to deep learning systems, and complicate the IB theory of deep learning by demonstrating instances where representation compression and generalization performance can diverge.
The quest for deeper understanding continues!
The impact of activation function choice
The starting point for our analysis is the observation that changing the activation function can markedly change the trajectory of a network in the information plane.
The authors used code supplied by Schwartz-Vis and Tishby to first replicate the results that we saw last week (Fig 1A below), and then changed the network to use ReLU instead — rectified linear activation functions . The resulting information plane dynamics are show in Fig 1B.
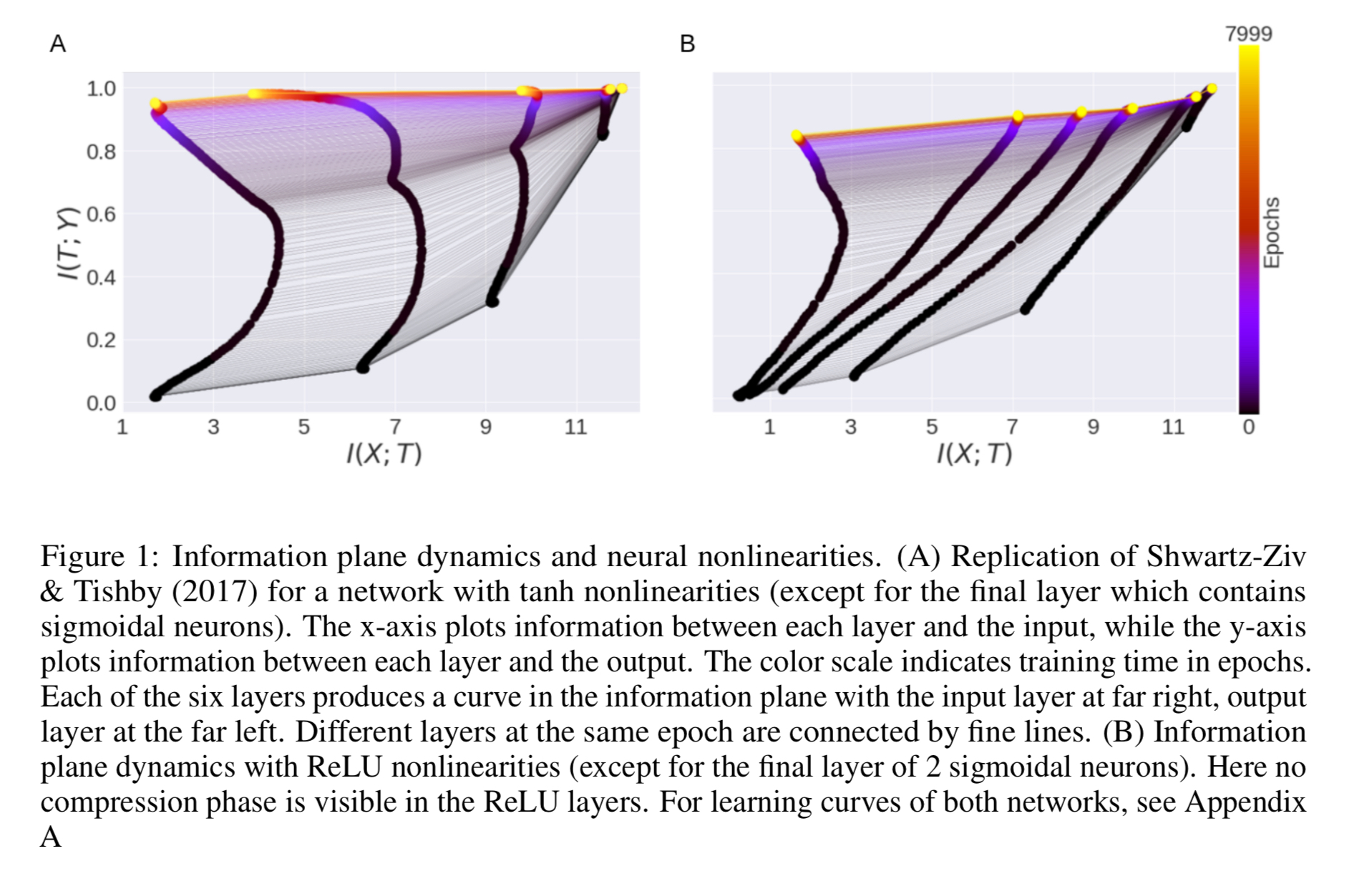
The phase shift that we saw with the original tanh activation functions disappears!
The mutual information with the input monotonically increases in all ReLu layers, with no apparent compression phase. Thus, the choice of nonlinearity substantively affects the dynamics in the information plane.
Using a very simple three neuron network, the authors explore this phenomenon further. A scalar Gaussian input distribution is fed through a scalar first layer weight
and passed through a neural nonlinearity
to yield hidden unit activity
.
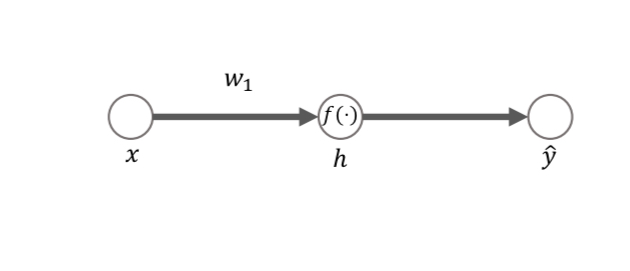
In order to calculate the mutual information, the hidden unit activity is binned into 30 uniform bins, to yield the discrete variable
.
With the tanh nonlinearity, mutual information first increases and then decreases. With the ReLU nonlinearity it always increases.
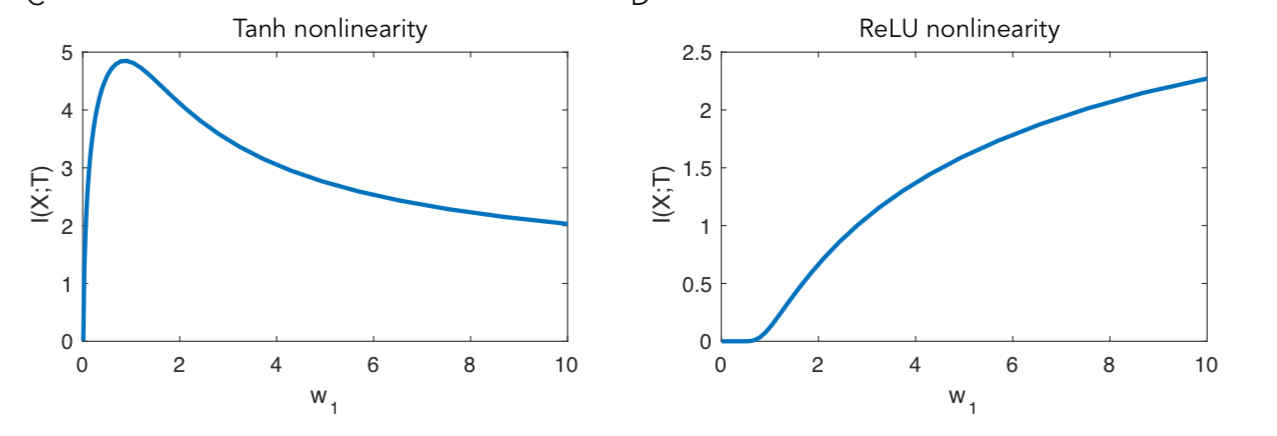
What’s happening is that with large weights, the tanh function saturates, falling back to providing mutual information with the input of approximately 1 bit (i.e, the discrete variable concentrates in just two bins around 1 and -1). With the ReLU though, half of the inputs are negative and land in the bin around 0, but the other half are Gaussian distributed and have entropy that increases with the size of weight. So it turns out that this double saturating nature of tanh is central to the original results.
… double-saturating nonlinearities can lead to compression of information about the input, as hidden units enter their saturation regime, due to the binning procedure used to calculate mutual information. We note that this binning procedure can be viewed as implicitly adding noise to the hidden layer activity: a range of X values map to a single bin, such that the mapping between X and T is no longer perfectly invertible.
The binning procedure is crucial for the information theoretic analysis, “however, this noise is not added in practice either during training or testing in these neural networks.”
The saturation of tanh explains the presence of the compression period where mutual information decreases, and also explains why training slows down as tanh networks enter their compression phase: some fraction of inputs have saturated the nonlinearities, reducing backpropagated error gradients.
Generalisation independent of compression
Next the authors use the information plane lens to further study the relationship between compression and generalisation.
… we exploit recent results on the generalization dynamics in simple linear networks trained in an student-teacher setup (Seung et al., 1992; Advani & Saxe, 2017). This setting allows exact calculation of the generalization performance of the network, exact calculation of the mutual information of the representation (without any binning procedure), and, though we do not do so here, direct comparison to the IB bound which is already known for linear Gaussian problems.
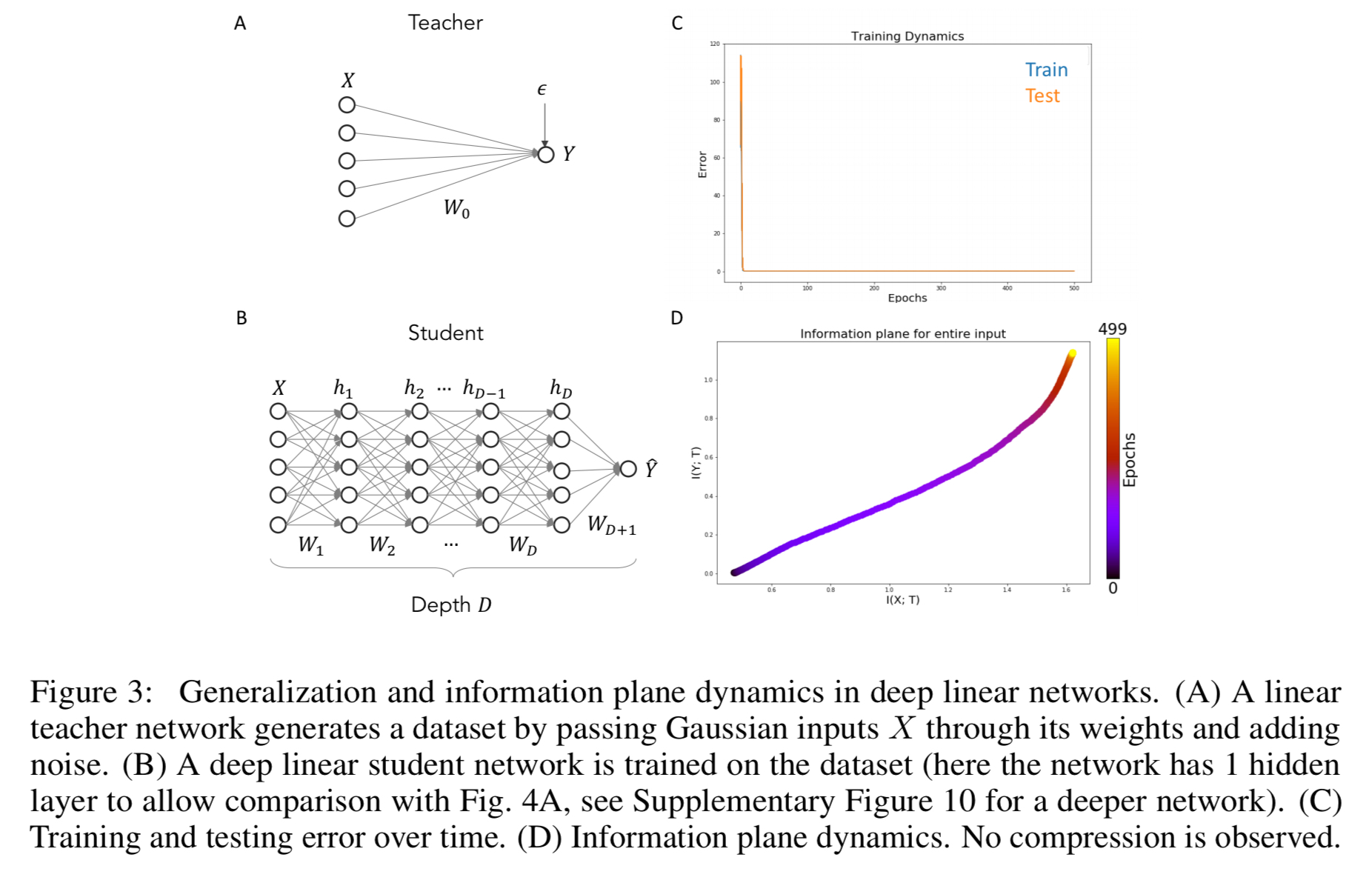
No compression is observed in the information plane (panel D in the figure above), although the network does learn a map that generalise well on the task and shows minimal overtraining. Experimentation to force varying degrees of overfitting shows networks with similar behaviour in the information plane can nevertheless have differing generalisation performance.
This establishes a dissociation between behavior in the information plane and generalization dynamics: networks that compress may or may not generalize well, and that networks that do not compress may or may not generalize well.
Does randomness help compression?
Next the authors investigate what contributes to compression in the first place, looking at the differences in the information plane between stochastic gradient descent and batch gradient descent. Whereas SGD takes a sample from the dataset and calculates the error gradient with respect to it, batch gradient descent uses the total error across all examples — “and crucially, therefore has no randomness or diffusion-like behaviour in its updates.”
Both tanh and linear networks are trained with both SGD and BGD, and the resulting information plane dynamics look like this:
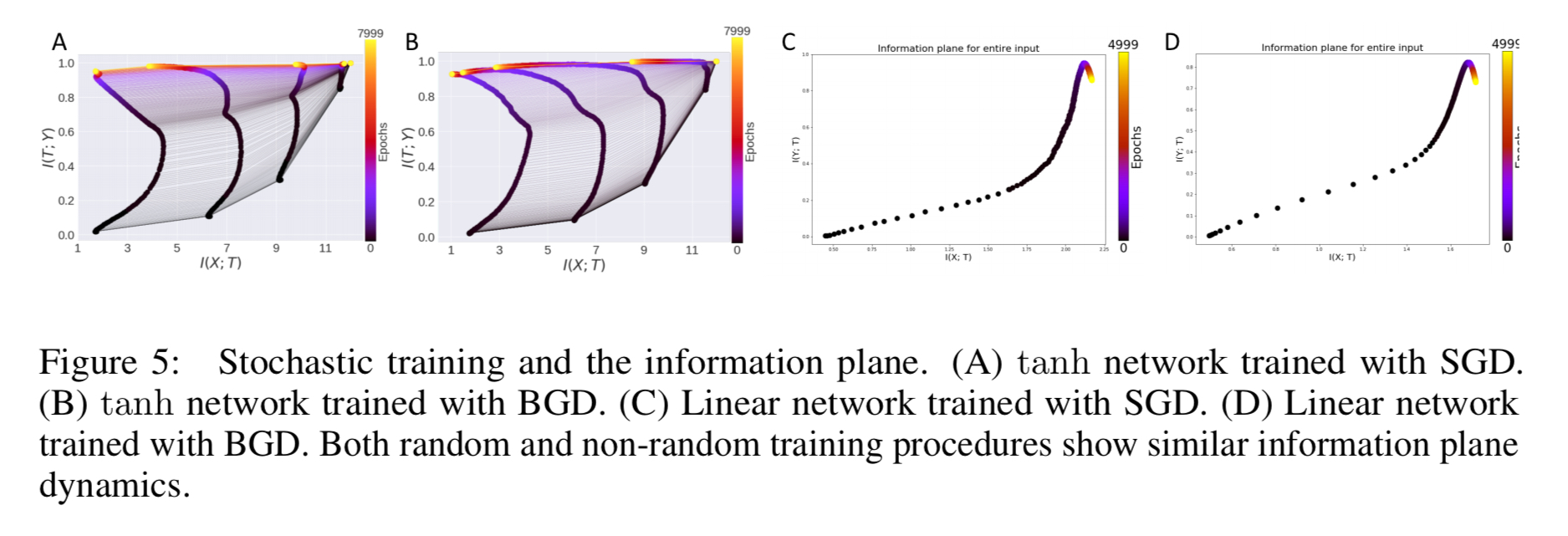
We find largely consistent information dynamics in both instances, with robust compression in tanh networks for both methods. Thus randomness in the training process does not appear to contributed substantially to compression of information about the input. This finding is consistent with the view presented in §2 that compression arises predominantly from the double saturating nonlinearity.
(Which seems to pretty much rule out the hope from the Schwartz-Viz & Tishby paper that we would find alternatives to SGD that support better diffusion and faster training).
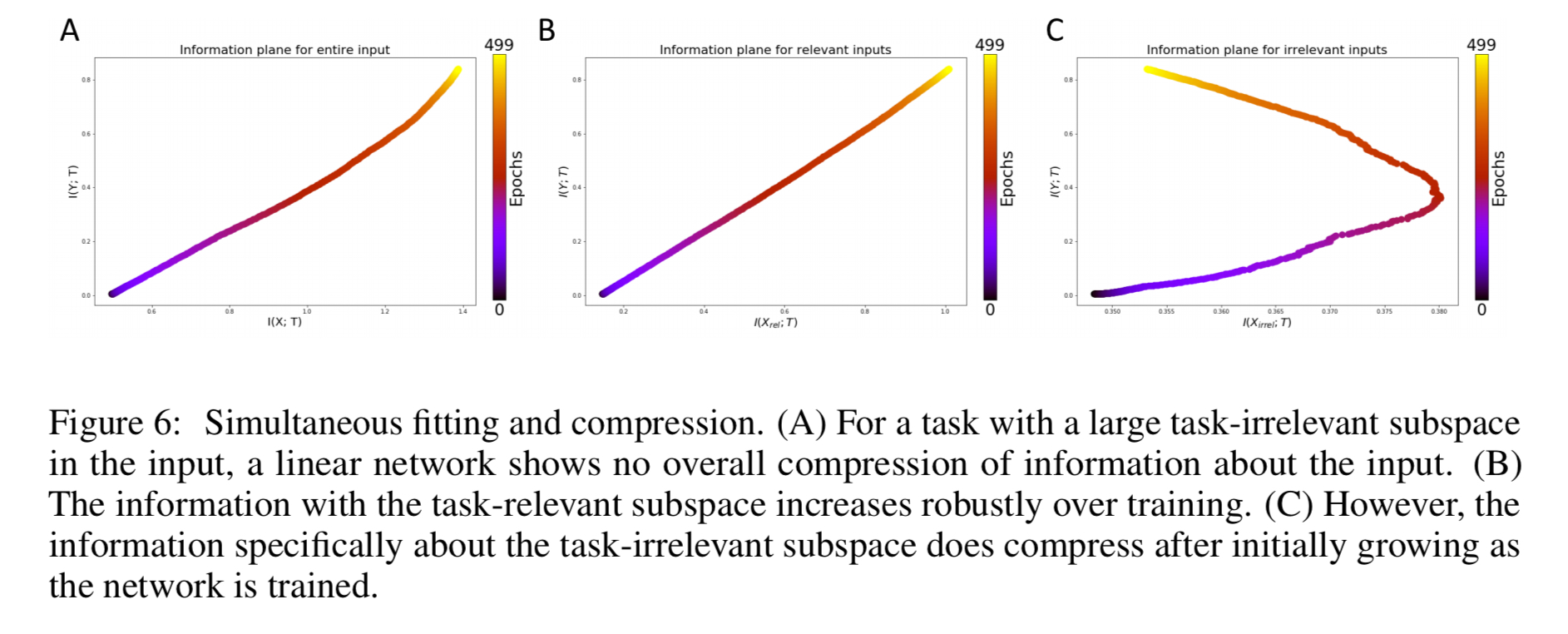
The compression of task-irrelevant information
A final experiment partitions the input X into a set of task-relevant inputs and a known to be task_irrelevant_ inputs. The former contribute signal therefore, while the latter only contribute noise. Thus good generalisation would seem to require ignoring the noise. The authors found that information for the task-irrelevant subspace does compress, at the same time as fitting is occurring for the task-relevant information, even though overall there is no observable compression phase.
The bottom line
Our results suggest that compression dynamics in the information plane are not a general feature of deep networks, but are critically influenced by the nonlinearities employed by the network… information compression may parallel the situation with sharp minima; although empirical evidence has shown a correlation with generalization error in certain settings and architectures; further theoretical analysis has shown that sharp minima can in fact generalize well.
You should also definitely check the replies and replies to replies to this paper – https://openreview.net/forum?id=ry_WPG-A-
“Blind submission to ICLR’18”: it’s not blind anymore, since you have published it in the open. By doing so, the authors have broken the rules of blind submission. I expect the PC chair will be very unhappy.
I think there might be a misunderstanding here. Sathiya Keerthi told me about the ICLR’18 submission, but that in no way means or implies he is an author – all submissions are available on the openreview system and there’s been quite a bit of discussion about this one. So it’s public domain that such a submission exists.
I take the viewpoint that layer after layer the nonlinearity compounds. Leading to something like chaos theory with bifurcations. Ie. The weighed sums in the net cannot entirely cancel out the nonlinearities introduced by the activation functions.
Another effect of nonlinear activation functions is guaranteed information loss. As the input information empties out layer after layer the net is put on a fixed trajectory with no further possibility of the input information further influencing matters. Unless you use something like ResNet where maintain some connection to the input.
Thanks to EDGE, a recently proposed scalable and optimal estimator of Mutual Information, It is shown that the Information Bottleneck theory of deep learning, proposed by Naftali Tishby, applies for a wide range of activations such as ReLU and Maxpooling!
Click to access 1801.09125.pdf