Opening the black box of deep neural networks via information – part I

~ Adrian Colyer

Opening the black box of deep neural networks via information Schwartz-Viz & Tishby, ICRI-CI 2017

In my view, this paper fully justifies all of the excitement surrounding it. We get three things here: (i) a theory we can use to reason about what happens during deep learning, (ii) a study of DNN learning during training based on that theory, which sheds a lot of light on what is happening inside, and (iii) some hints for how the results can be applied to improve the efficiency of deep learning – which might even end up displacing SGD in the later phases of training.

Despite their great success, there is still no comprehensive understanding of the optimization process or the internal organization of DNNs, and they are often criticized for being used as mysterious “black boxes”.

I was worried that the paper would be full of impenetrable math, but with full credit to the authors it’s actually highly readable. It’s worth taking the time to digest what the paper is telling us, so I’m going to split my coverage into two parts, looking at the theory today, and the DNN learning analysis & visualisations tomorrow.

An information theory of deep learning

Consider the supervised learning problem whereby we are given inputs x \in X and we want to predict labels y \in Y. Inside the network we are learning some representation T(X) of the input patterns, that we hope enables good predictions. We also want good generalisation, not overfitting.

Think of a whole layer T as a single random variable. We can describe this layer by two distributions: the encoder P(T|X) and the decoder P(Y|T).

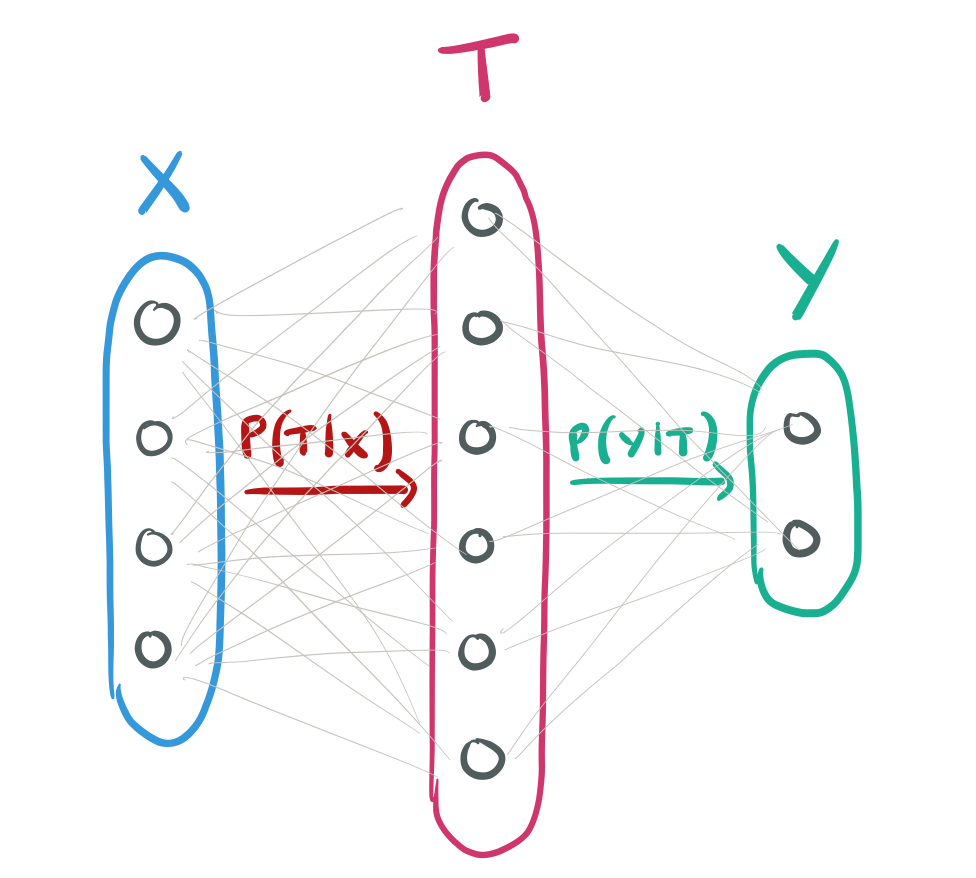
So long as these transformations preserve information, we don’t really care which individual neurons within the layers encode which features of the input. We can capture this idea by thinking about the mutual information of T with the input X and the desired output Y.

Given two random variables X and Y, their mutual information I(X;Y) is defined based on information theory as
\displaystyle I(X;Y) = H(X) - H(X|Y)

Where H(X) is the entropy of X and H(X|Y) is the conditional entropy of X given Y.

The mutual information quantifies the number of relevant bits that the input X contains about the label Y, on average.

If we put a hidden layer T between X and Y then T is mapped to a point in the information plane with coordinates (I(X;T), I(T;Y)). The Data Processing Inequality (DPI) result tells us that for any 3 variables forming a Markov chain X \rightarrow Y \rightarrow Z we have I(X;Y) \geq I(X;Z).

So far we’ve just been considering a single hidden layer. To make a deep neural network we need lots of layers! We can think of a Markov chain of K-layers, where T^i denotes the i^{th} hidden layer.

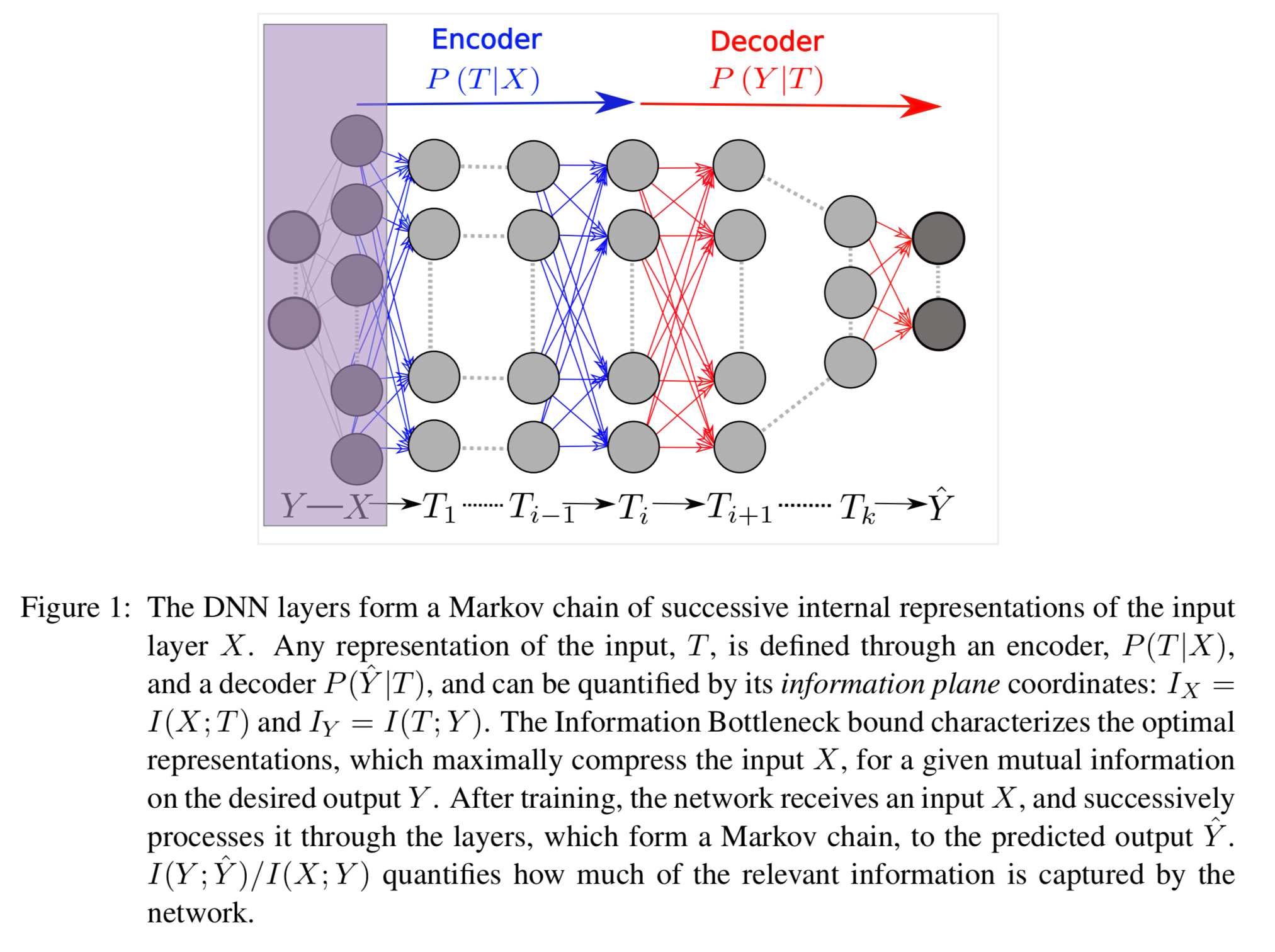
In such a network there is a unique information path which satisfies the DPI chains:

\displaystyle I(X;Y) \geq I(T_1;Y) \geq I(T_2;Y) \geq ... \geq I(T_k;Y) \geq I(\hat{Y};Y)

and
\displaystyle H(X) \geq I(X;T_1) \geq I(X;T_2) \geq ... \geq I(X;T_k) \geq I(X;\hat{Y})

Now we bring in another property of mutual information; it is invariant in the face of invertible transformations:

\displaystyle I(X;Y) = I(\psi (X); \phi(Y))

for any invertible functions \psi and \phi.

And this reveals that the same information paths can be realised in many different ways:

Since layers related by invertible re-parameterization appear in the same point, each information path in the plane corresponds to many different DNN’s , with possibly very different architectures.

Information bottlenecks and optimal representations

An optimal encoder of the mutual information I(X;Y) would create a representation of a minimal sufficient statistic of X with respect to Y. If we have a minimal sufficient statistic then we can decode the relevant information with the smallest number of binary questions. (That is, it creates the most compact encoding that still enables us to predict Y as accurately as possible).

The Information Bottleneck (IB) tradeoff Tishby et al. (1999) provides a computational framework for finding approximate minimal sufficient statistics. That is, the optimal tradeoff between the compression of X and the prediction of Y.

The Information Bottleneck tradeoff is formulated by the following optimization problem, carried independently for the distributions, p(t|x), p(t), p(y|t), with the Markov chain: Y \rightarrow X \rightarrow T

\displaystyle \min_{p(t|x),p(y|t),p(t)} \{ I(X;T) - \beta I(T;Y)\}

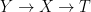
where the Lagrange multiplier \beta determines the level of relevant information captured by the representation T, I(T;Y).

The solution to this problem defines an information curve: a monotonic concave line of optimal representations that separates the achievable and unachievable regions in the information plane.

Noise makes it all work

Section 2.4 contains a discussion on the crucial role of noise in making the analysis useful (which sounds kind of odd on first reading!). I don’t fully understand this part, but here’s the gist:

The learning complexity is related to the number of relevant bits required from the input patterns X for a good enough prediction of the output label Y, or the minimal I(X; \hat{X}) under a constraint on I(\hat{X}; Y) given by the IB.

Without some noise (introduced for example by the use of sigmoid activation functions) the mutual information is simply the entropy H(Y) independent of the actual function we’re trying to learn, and nothing in the structure of the points p(y|x) gives us any hint as to the learning complexity of the rule. With some noise, the function turns into a stochastic rule, and we can escape this problem. Anyone with a lay-person’s explanation of why this works, please do post in the comments!

Setting the stage for Part II

With all this theory under our belts, we can go on to study the information paths of DNNs in the information plane. This is possible when we know the underlying distribution P(X,Y) and the encoder and decoder distributions P(T|X) and P(Y|T) can be calculated directly.

Our two order parameters, I(T; X) and I(T;Y), allow us to visualize and compare different network architectures in terms of their efficiency in preserving the relevant information in P(X;Y).

We’ll be looking at the following issues:

  1. What is SGD actually doing in the information plane?
  2. What effect does training sample size have on layers?
  3. What is the benefit of hidden layers?
  4. What is the final location of hidden layers?
  5. Do hidden layers form optimal IB representations?