SmartPool: Practical decentralized mining

SmartPool: Practical decentralized pooled mining Luu et al., USENIX Security 2017

Say you wanted to implement a mining pool that didn’t place power in the hands of centralized pool operators. If only there was some fully decentralised way of establishing trust and coordinating activities according to a policy, in which anyone could participate… Oh, wait, that sounds just like a smart contract!

In this work, we propose SmartPool, a novel protocol design for a decentralized mining pool. Our protocol shows how one can leverage smart contracts, autonomous blockchain programs, to decentralize cryptocurrency mining.

SmartPool is both a neat idea in its own right, and also a great case study in some of the considerations when designing smart contracts that we looked at last week. If you want to follow along at home, you can find the source code for the SmartPool contract on GitHub.

As part of their evaluation, the authors ran a SmartPool mining pool for a week with a peak hashrate of 30 GH/s, and mined 105 blocks costing miners just 0.6% of block rewards in transaction fees. Compare this to the 3% typically taken by centralized pools. (At the exchange rate on the day I’m writing this, 105 blocks comes out at just shy of $200K in miner rewards.)

Why do we care about decentralized mining pools?

The whole point was to be decentralized, but over time mining pools have come to hold increasing power in the Bitcoin and Ethereum networks: Bitcoin derives 95% of its mining power from just 10 pools, and Ethereum gets 80% of its mining power from only 6 pools. The consolidation of power leads to potential hijacking attacks, and threats to the core security of the Bitcoin consensus protocol if a single pool operator controls more than 51% of the mining power (as has happened in both Ethereum and Bitcoin on several occasions – e.g. DwarfPool and GHash.io respectively).

Pools can also dictate which transactions get included in the blockchain, increasing the threat of transaction censorship or favouring their own blocks.

For example, users recently publicly speculated that a large Ethereum pool favored its own transactions in its blocks to gain an advantage in a public crowdsale.

And then of course there are the comparatively hefty fees (~3%) to be paid to pool operators.

In Bitcoin, one decentralized mining pool solution does exist, called P2Pool, but as the authors demonstrate it suffers from a lack of scalability and has not been widely adopted.

Challenges for a decentralized mining pool

We consider the problem of building a decentralized protocol which allows a large open network to collectively solve a computational PoW puzzle, and distribute the earned reward between the participants proportional to their computational contributions.

Such a protocol should be decentralised, efficient, secure, and fair.

Decentralised – there should be no central operator managing the pool and its participants.
Efficient – running costs should be low and the variance and rewards for miners should be comparable to centralized solutions. Overheads and other costs (e.g., gas costs) incurred by participants must be reasonably small
Secure – protection from attackers wanting to steal rewards, game the system, or prevent others from joining
Fair – participants should receive rewards in proportion to their share of the contributions.

Assume a threat model in which miners are rational and can deviate arbitrarily from the honest protocol to gain more reward.

SmartPool high-level overview

At a high level, SmartPool replaces the mining pool operator with a smart contract. The smart contract acts as a trustless bookkeeper for the pool by storing all shares submitted by miners. When a new share is submitted, the contract verifies the validity of the share, checks that no previous record of the share exists, and then updates the corresponding miner’s record.

Here’s a starter for 10 which shows the basics of the idea:

Unfortunately this version has a number of shortcomings which we’ll need to fix (compare to e.g., the final contract source).

If there are a large number of shares in the pool, then an unwieldy number of messages will be sent to the contract. For example, if it takes 1,00,000 shares to mine a block, that’s 1,00,000 transactions. But reducing the number of shares per block increases the variance in reward for miners, defeating the point of pooling.
The gas fees incurred for submitting shares to the pool might cause miners to end up with negative rewards overall
Transactions are in plaintext, so network adversaries can see the transactions of other miners and either steal or resubmit the shares. (In centralized pools, a secure and private connection to the pool can be assumed, so this issue does not exist).
It’s difficult to use the SmartPool for e.g. Bitcoin mining when the contract is deployed on Ethereum. The contract must guarantee correct payments in Bitcoin, but Ethereum contracts operate only in Ether.

SmartPool is decentralised, efficient, secure, and fair:

Decentralised – the pool is implemented as a smart contract
Efficient – miners submit shares in batches (e.g., 1 transaction can claim 1 million shares). Miners do not need to submit data for all of the shares, but only a few for verification purposes.
Secure – miners must commit the right set of beneficiary addresses in a share before mining, so that it can’t be change after a solution is found.
Fair – a probabilistic verification of miner submissions aided by a Merkle-tree based commitment scheme guarantees the same average outcome as running a full verification.

To handle the case of Bitcoin mining on top of Ethereum, SmartPool leverages the Bitcoin coinbase transaction so that miners don’t need to trust a third party to proxy the payment. Miners do still need to pay for gas in Ether. Gas payments should be less than 1% of the total miners’ reward.

SmartPool maintains two main lists in its contract state – claim list claimList and a verified claim list verClaimList.

When a miner submits a set of shares as a claim for the current block, it is added to the claim list. This acts as a cryptographic commitment to the shares claimed to be found by the miner.
SmartPool verifies the validity of the claim, and once verified, moves it to the verified claim list. Claim verification and payments for verified claims happen in a single atomic transaction.

Submitted claims therefore need to include sufficient metadata for verification purposes. Enabling efficient verification is one of the key contributions of the paper.

The goal of the verification process is to prevent miners from both submitting invalid shares and over-claiming the number of shares they have found.

The claim data structure is a cryptographic commitment to the shares being claimed, based on an augmented Merkle tree structure we’ll look at next. We want to verify that (i) all submitted shares are valid, (ii) no share is repeated twice in a claim, and (iii) each share appears in at most one claim.

For efficiency, SmartPool uses a simple but powerful observation: if we probabilistically verify the claims of a miner, and pay only if no cheating is detected, then expected payoffs of cheating miners are the same or less than those of honest miners. In effect, this observation reduces the effort of verifying millions of shares down to verifying one or two!

Here’s the high level intuition. Consider a cheating miner submitting a claim to 1000 shares, but which contains only 500 valid shares. If SmartPool randomly samples only one share, then the odds of the cheating being detected are 1/2. If the miner is caught cheating, they get paid nothing. If he gets lucky and is not detected, he gets rewarded for 1000 shares. Hence the expected payoff is still 500 – exactly the same as if an honest miner claimed the right number of shares.

By sampling $k \geq 1$ times, SmartPool can reduce the probability of a cheater remaining undetected exponentially small in $k$ .

The Augmented Merkle tree

The data structure containing the submitted claims that makes all this possible is an augmented Merkle tree. The Merkle tree part of this enables us to commit to a batch of shares in a single claim, the augmented part verifies that the committed set of claims have increasing counters. All shares must include a counter, which must be strictly increasing with each share, and the shares must be included in the tree in increasing counter order, left-to-right.

Here are the rules:

Let $ctr$ be a one-to-one function mapping shares to integers. Then an augmented Merkle tree for a set of objects $S = \{s_1, s_2, ..., s_n\}$ is a tree whose nodes $x$ have the form $(min(x), hash(x), max(x))$ where:

$min(x)$ is the minimum of the children’s min (or $ctr(s_i)$ if $x$ is a leaf corresponding to the object $s_i$ ).
$hash(x)$ is the cryptographic hash of the concatenation of the children nodes (or $hash(s_i)$ if $x$ is a leaf corresponding to the object $s_i$ )
$max(x)$ is the maximum of the children’s min (or $ctr(s_i)$ if $x$ is a leaf corresponding to the object $s_i$ )

A picture is in order! Here I’m using 16-bit hashes for convenience of illustration.

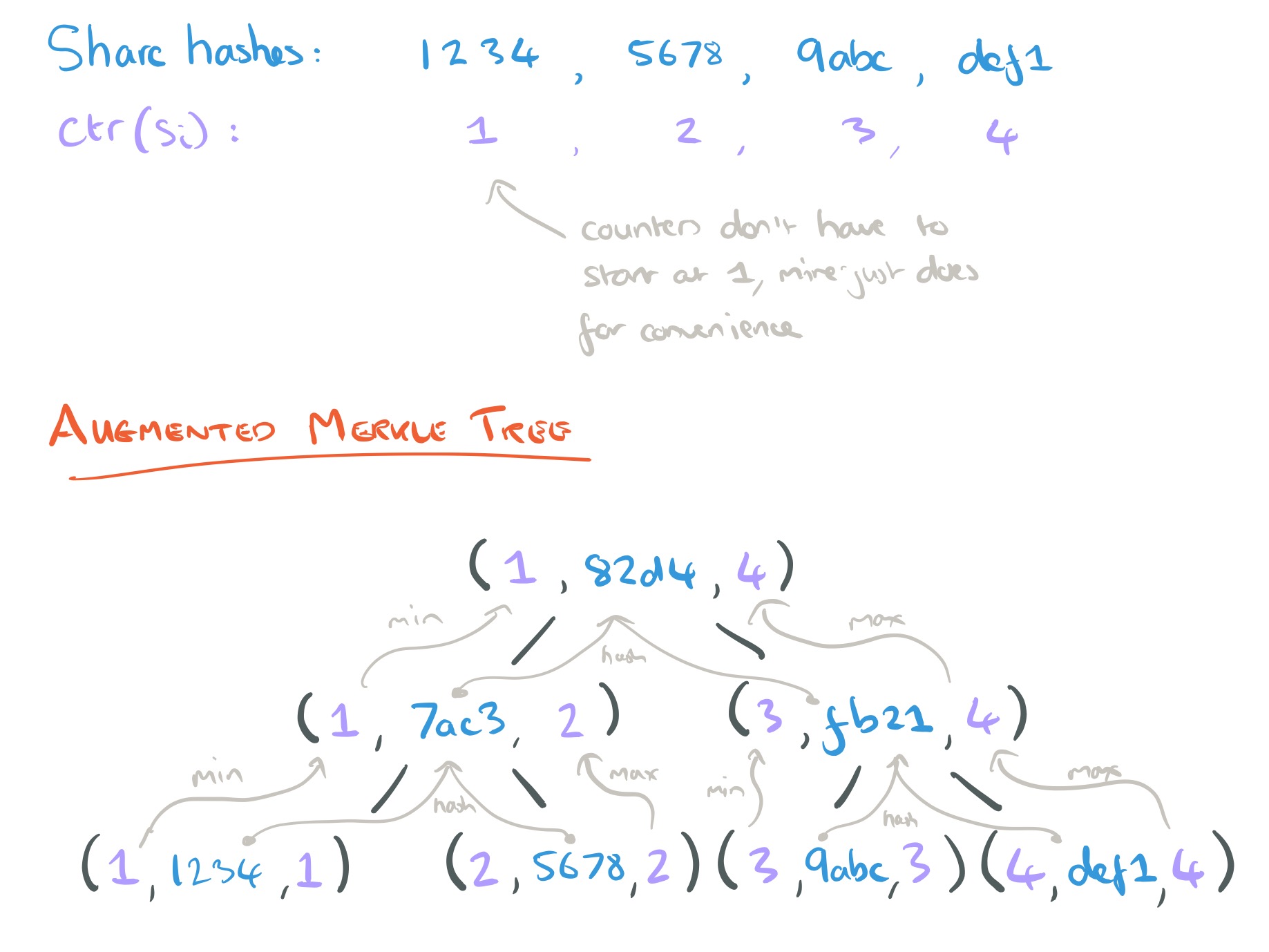
And then after I’d drawn that, I noticed the paper also includes the following figure – but I think mine is prettier!

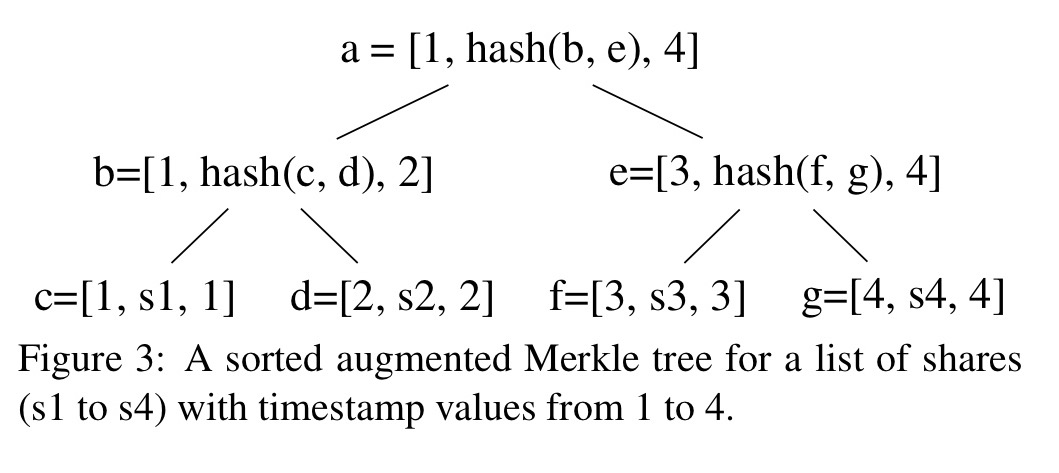
In the figure above, to prove that share c has been committed, a miner has to submit two nodes d and e to SmartPool. SmartPool can reconstruct the other nodes on the path from c to the root. The proof for one share in a Merkle tree of height h contains h hashes.

Any duplicated shares in a claim will yield a sorting error in at least one path of the augmented Merkle tree.

Thus, by sampling the tree in a constant number of leaves and checking their corresponding paths, with high probability we will detect a sorting error in the augmented Merkle tree if there is one.

To prevent miners from submitting the same shares in two different claims, things are set up so that the maximum counter value in an earlier submission is always smaller than the minimum counter of shares in a later one. For example, the pair (block-timestamp, nonce) can be used as counter in an Ethereum block.

To get a random seed for sampling, the hashes of future blocks can be used.

Here’s the full protocol so far:

(Enlarge).

Is it fair?

Section 4 contains an analysis proving the following theorem:

Let A be a Merkle tree. If A is sorted, then all paths in A are valid. If A is not sorted, then every leaf containing a sorting error lies on an invalid path.

The corollaries are:

Every Merkle tree has at least as many invalid paths as sorting errors among the leaves. In particular, there are at least as many invalid paths as there are duplicate values among the leaves.
Under the payment scheme (no payout if caught cheating), if SmartPool checks one random path in the augmented Merkle tree of a claim, the expected reward when submitting invalid or duplicate shares is the same as the expected reward when submitting only valid shares.

An against an adversary;

If an adversary controls less than 50% of Ethereum hash power, then it suffices to sample only two paths of the augmented Merkle tree based on two consecutive blocks to pay miners fairly, on average.

Implementation details

Section 6 details the implementation and the results from a week of mining. There are a few extra important details here not included in the main body of the text:

The need to implement the Ethash function in the contract in order to verify that a block header satisfies the required difficulty (this accounts for a lot of the code you see in the source).
How to avoid paying excessive costs to store the Ethereum dataset (needed for Ethash) in the contract – storing the full dataset, which changes every four days, would cost about 3M USD/day as of June 2017!
How to handle coinbase transactions in Bitcoin.

The appendix discusses the intriguing possibility of a cryptocurrency in which SmartPool is deployed natively as the only mining pool.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic