DStress: Efficient differentially private computations on distributed data

~ Adrian Colyer

DStress: Efficient differentially private computations on distributed data Papadimitriou et al., EuroSys’17

Regulators would like to assess and manage the systemic risk in the banking system – for example, the likelihood that a few initial bankruptcies could cause a failure cascade.

In theory, it would be possible to quantify the risk of such a cascading failure by looking at the graph of financial dependencies between the banks, and in fact economists have already developed a number of metrics that could be used to quantify this “systemic” risk…

But in practice current audits are way less sophisticated than this. The information required to build the graph is extremely sensitive, and the banks prefer not to share it even with the government, let alone with each other!

In a recent working paper, the Office of Financial Research (OFR) has started investigating ways to perform system-wide stress tests while protecting confidentiality.

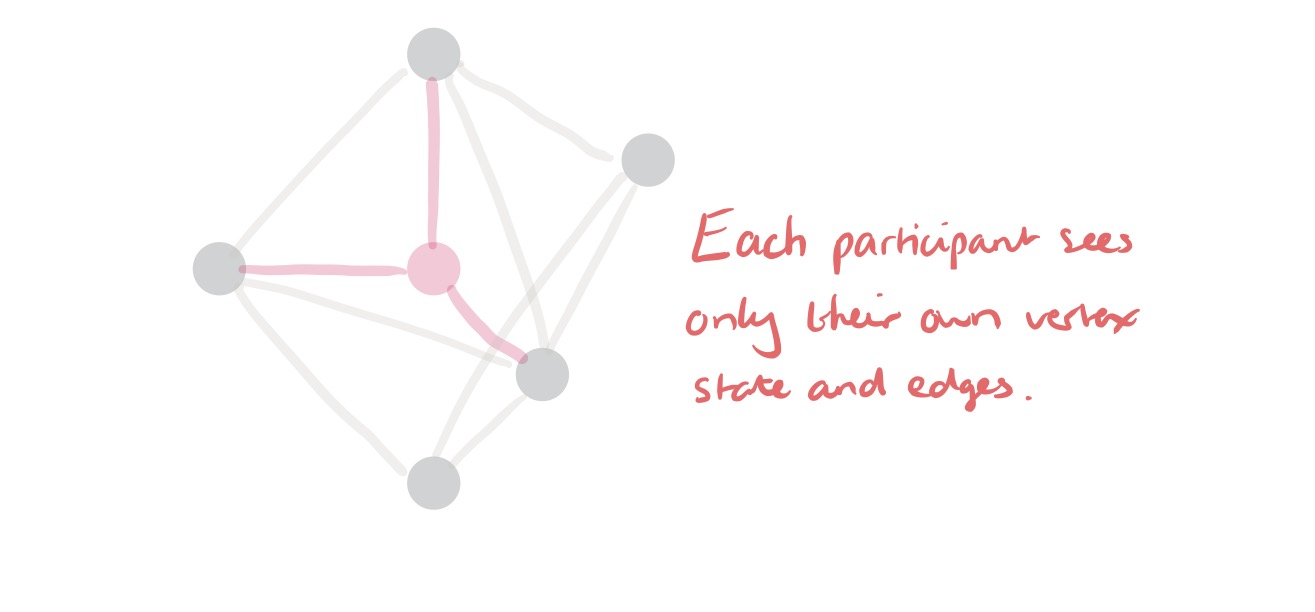
We can cast this as an instance of a really interesting computer science problem. Let there be N participants P_i in a network (directed graph) G. Each participant knows the properties of its own vertex, v_i, and the properties of any edges that begin or end at v_i. We want to collectively compute a function F(G) such that:

  • Each participant learns nothing of the vertex properties of other participants (value privacy).
  • The presence or absence of an edge (v_i, v_j) is not revealed to participants other than i and j (edge privacy).
  • The final output F(G) does not reveal too much information (we’ll use differential privacy to define this) about individual vertices or edges in G.

This fits the systemic risk calculation nicely – each financial institution is represented by a vertex, and the edges represent agreements between financial institutions. The function to be computed, F(G) is of course the systemic risk calculation. This calculation will be run in a distributed fashion, with each institution hosting a node for its own vertex. DStress provides a solution that meets all of these constraints, coupled with efficient execution. There are other applications beyond systemic risk calculation too:

… Not all of these [graph] algorithms have privacy constraints, but there are many that do; for instance, cloud reliability, criminal intelligence, and social science all involve analyzing graphs that can span multiple administrative domains.

Building blocks

To meet all of its privacy obligations, DStress depends on three fundamental building blocks:

  • Differential privacy is used to achieve output (F(G)) privacy. It provides strong, provable privacy guarantees which should be reassuring to banks. As we’ve seen before, the core mechanism is the addition of small amounts of random noise – coupled with careful analysis to understand just how much noise to add such that a certain level of privacy is achieved. Under differential privacy, small changes to inputs (i.e., the addition or removal of one data point) only have a statistically negligible effect on the output distribution.
  • Secure multiparty computation (MPC) enables a set of mutually distrustful parties to evaluate a function f over some confidential input data x, such that no party can learn anything about x other than what the output y = f(x) reveals. DStress uses MPC to perform vertex calculations and aggregations without leaking any information from one vertex (bank) to others.

In the specific protocol we use (GMW), each party i initially holds a share x_i of the input x such that x = \oplus_i x_i (in other words the input can be obtained by XORing all the shares together), and after the protocol terminates, each party similarly hold a share y_i of the ouput y = f(x)… GMW is collusion-resistant in the sense that, if k + 1 parties participate in the protocol, the confidentiality of x is protected as long as no more than k or the parties collude.

  • ElGamal encryption is an encryption scheme that provides for both additive homomorphism and the ability to re-randomize public keys. DStress depends on both of these abilities.

ElGamal itself has multplicative homomorphism : if you encrypt two messages m_1 and m_2 , multiply the resulting ciphertexts together, and then decrypt the result, you are left with m_1.m_2. This can be turned into additive homomorphism by encrypting not just the message m but instead g^m: the product of two ciphertexts g^{m_1}.g^{m_2} = g^{m_1 + m_2} now decrypts to the sum of the underlying messages. Further, if g^x is a public key, it can be re-randomizing by raising it to some power r, yielding a new public key g^{xr}. Decryption can be done with the original private key x by raising the ephemeral key in the ciphertext to r as well. Both operations can be performed without knowledge of the private key x.

DStress: Putting it all together

DStress runs vertex programs. Each vertex has an initial state and an update function. In each iteration the update function is run for each vertex v which outputs a new vertex state s_v and a message for every neighbour of v in G. (A no-op message can be sent if there is no data to send). After this computation step, each vertex sends its messages along its edges to its neighbours in a communication step. Recipients use these messages as additional inputs for their next computation step. After n iterations, DStress invokes an aggregation function, A which reads the final state of each node and combines the states into a single output value. Noise is drawn from a Laplace distribution (for differential privacy) and added to the output value to yield the overall result of the computation.

DStress runs in distributed fashion across a number of nodes:

We expect that, for privacy reasons, each participant would want to operate its own node, so that it does not have to reveal its initial state to another party.

No node can be allowed to see intermediate computation results – not even those of its own vertex. DStress uses shares from the GMW secure multiparty computation protocol to achieve this:

… DStress associates each node i with a set B_i of other nodes that we refer to as the block of i. The members of the block each hold a share of the vertex’s current state, and they use MPC to update the state based on incoming messages. To prevent colluding nodes from learning the state of a vertex, each block contains k + 1 nodes, where k is the collusion bound we have assumed.

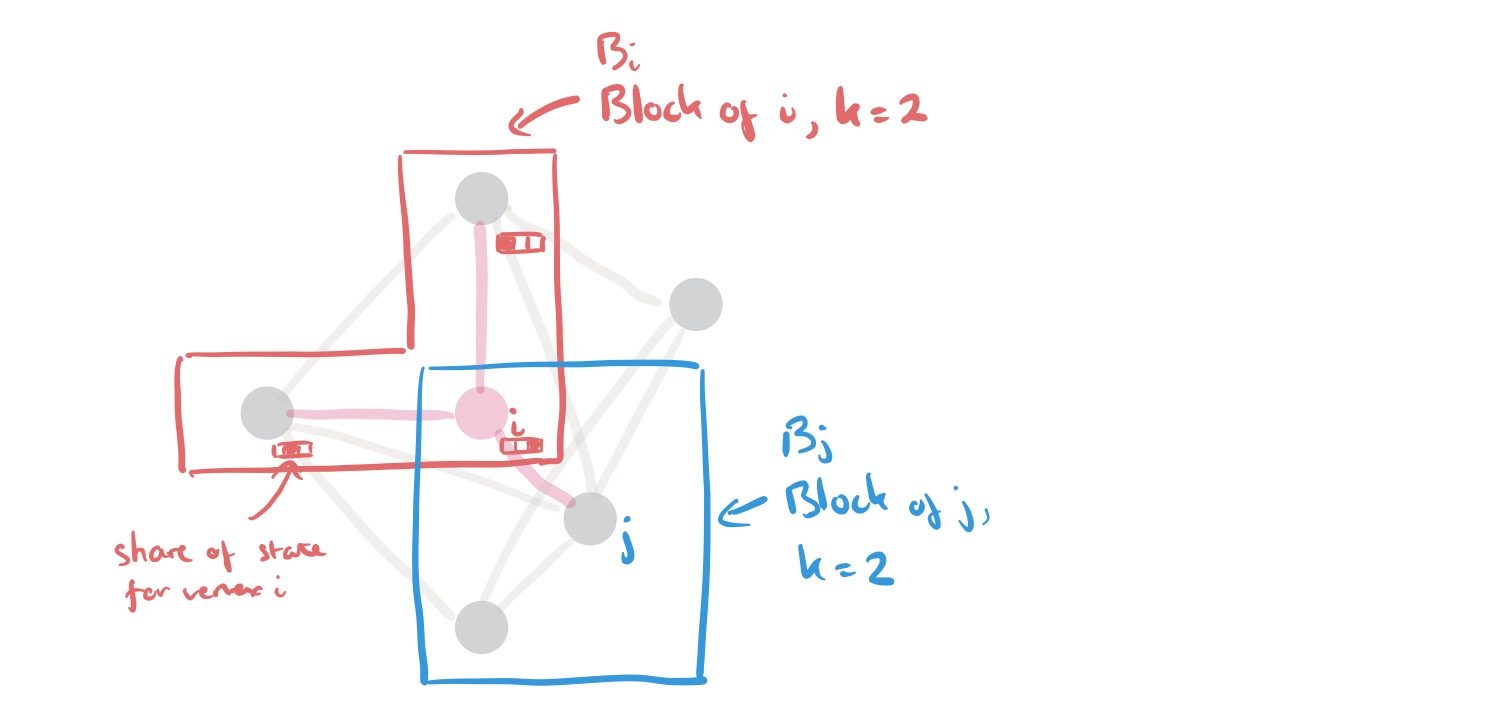
(In the sketch above, I happen to show the blocks for i and j overlapping, but there’s no reason this has to be the case).

A one-time setup step coordinated by a trusted party (e.g., a regulator) associates each node with a block containing k + 1 different nodes, and gives the block D different sets of public keys, where D is a publicly known upper bound on the degree of any node in the graph. This can all be done without the trusted party ever learning the topology of the graph.

At the start of the algorithm, each node loads the initial state of its local vertex together with D copies of the no-op message (there are no real messages yet), and splits each of those messages into |B_i| shares, one for each member of its block.

We now perform n iterations (fixed in advance with an n chosen to give convergence with high likelihood) of the computation and communication steps.

  1. In the computation step the members of block B_i use MPC to evaluate the update function of the vertex v_i. The circuit has inputs for the D messages and the current state of v_i, as well as outputs for D output messages and the new state of v_i. All inputs and outputs remain divided into shares and are never revealed to any individual node.
  2. In the communication step messages are sent along the corresponding edges of the graph, using a protocol we’ll look at next

After the n iterations, a special aggregation block B_A is used to compute the final evaluation function and add the noise.

Each block sends its state shares and some random shares to B_A; the members of B_A then use MPC to a) evaluate A on the states; b) combine the random shares to get a random input seed, c) draw a noise term from the Lap(s/ε) using the seed; and d) output the sum of that term and the result of A.

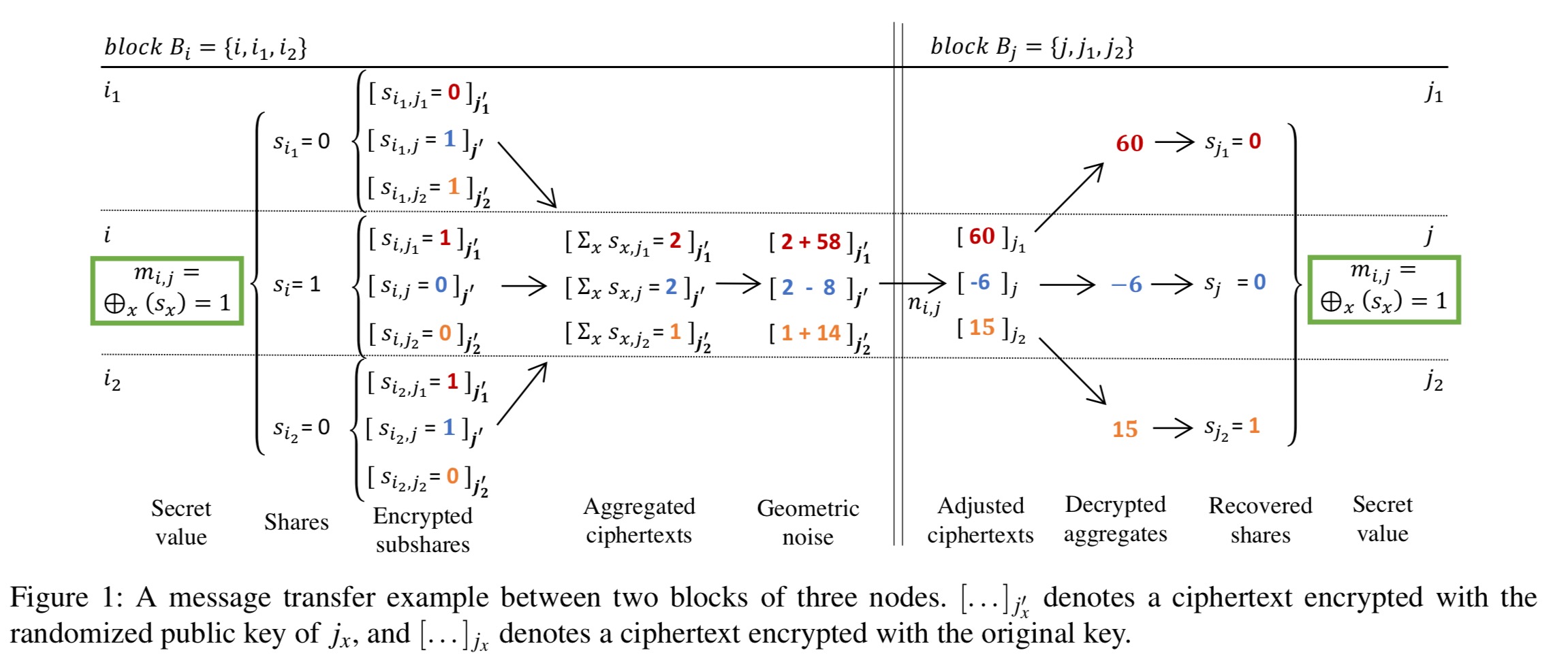
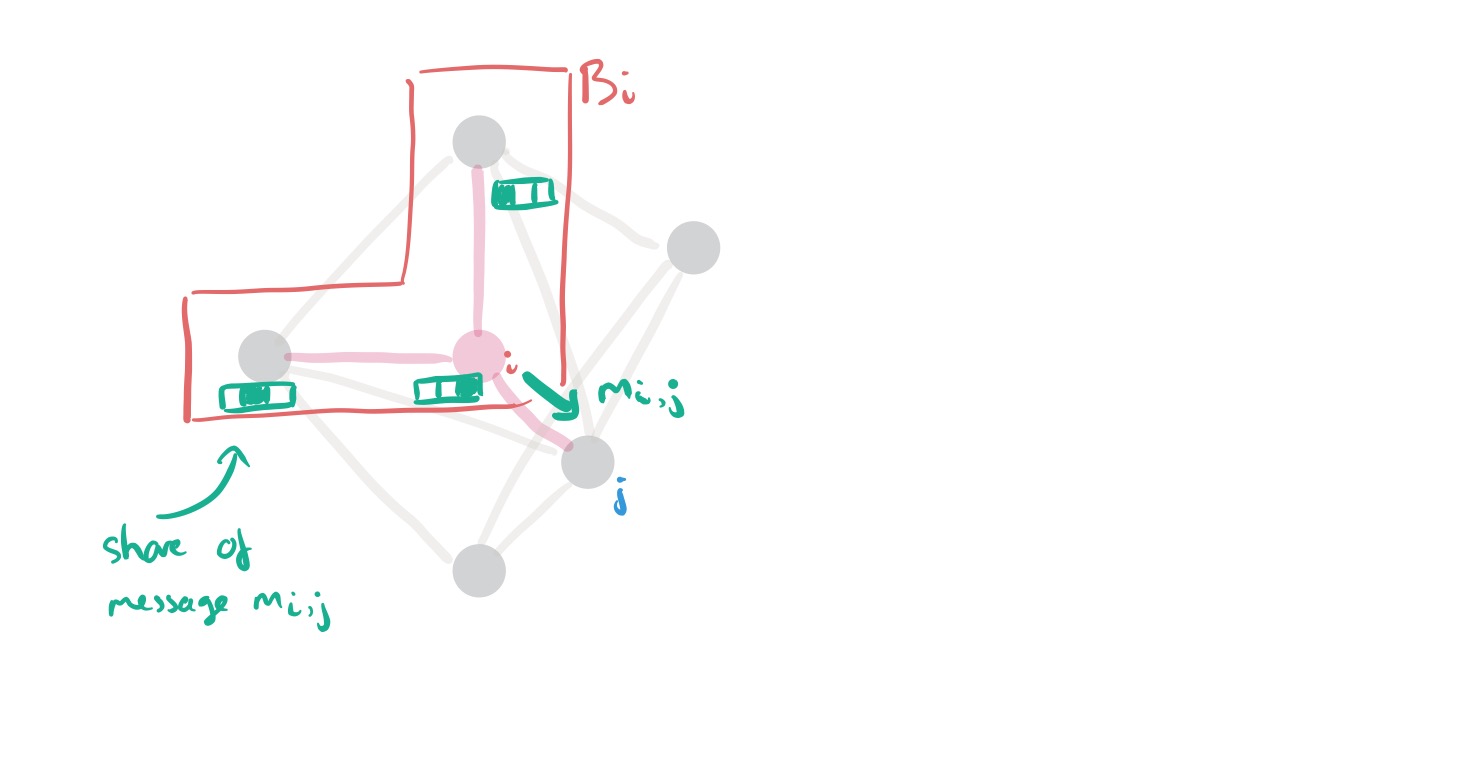
How DStress sends messages between vertices

Each member of a block B_i holds one share of a message m_{i,j} that is to be sent along the edge from i to j. At the end of the message transfer, we want each member of block B_j to hold one share of the message.

The basic idea is for each member of B_i to pick a different public key from j’s block certificate, encrypt its share of the message using that key, and forward the encrypted ciphertext to i, who forwards them to j. j can adjust the ephemeral keys in the ciphertexts using neighbour keys n_{i,j} and forward them to the members of B_j.

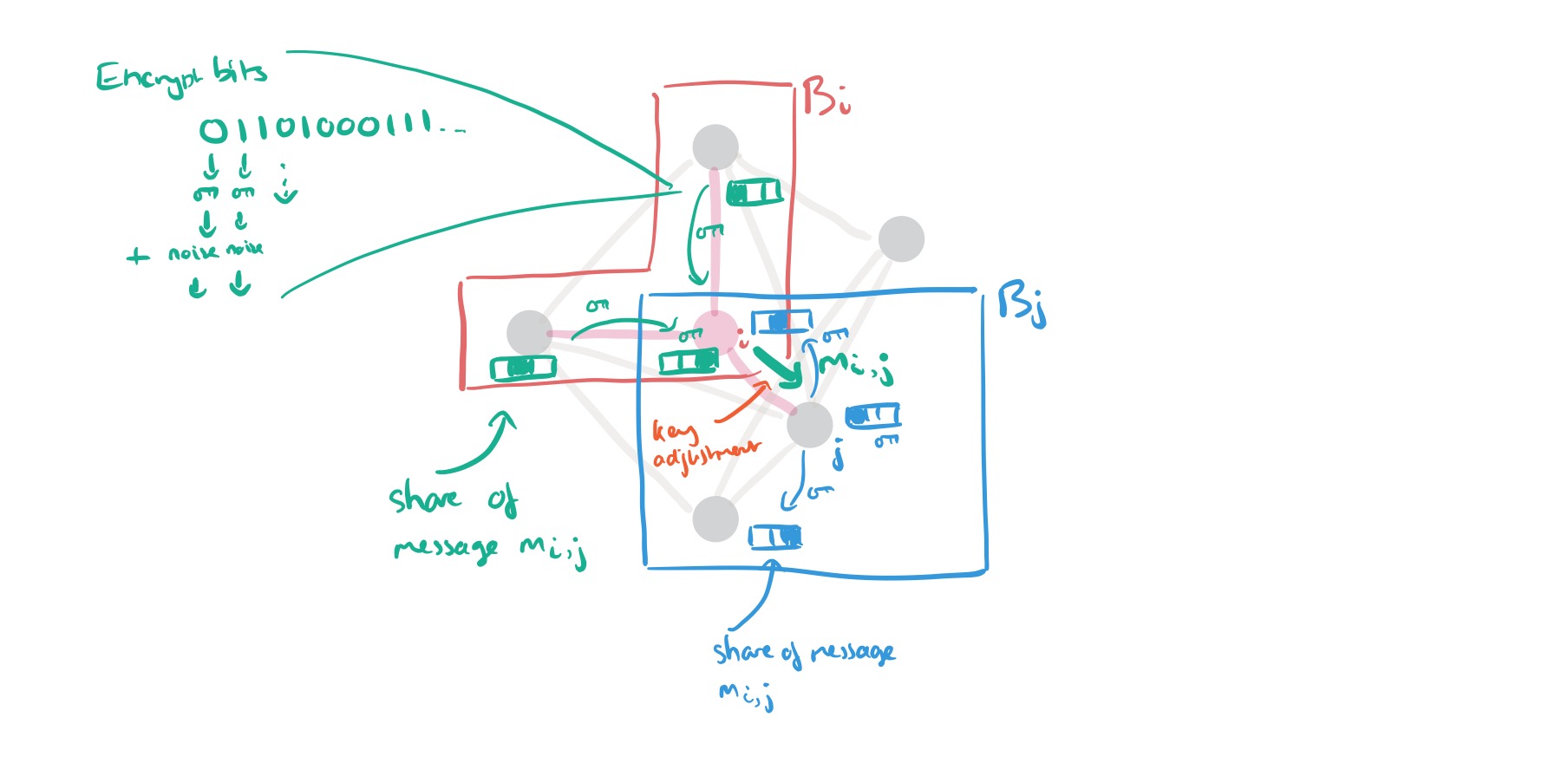
If a node happens to be a member of both blocks though (as in my sketch above), it can potentially learn two shares this way. To prevent this we make a tweak whereby each share is itself split into k+1 subshares, and these subshares are then split into individual bits, each encrypted separately. Before forwarding to B_j via j, i homomorphically adds an even random number to each encrypted bit. (See section 3.5 in the paper for the full details). Members of B_j decrypt the sums and set their bit share to 0 iff the sum is even. Altogether it looks like this:

Demonstrating feasibility.

The authors show how to map two existing systemic risk algorithms from the literature onto DStress’ programming model. Here’s one of them as an example (see section 4.2 for a brief description of the original algorithm).

The output of the computation is a measure called the total dollar shortfall (TDS) – the amount of extra money the government would need to make available to prevent failures. Adding noise to TDS results in dollar-differential privacy.

An evaluation is run on Amazon EC2 using 100 m3.xlarge instances. From that data gathered there, it is possible to estimate the costs for running a systemic risk calculation for the roughly 1,750 commercial banks in the United States. A degree bound of D = 100 is used, and k is set to 20 (the largest known colluding network to date had 16 member banks). The projected costs for the computation are shown in the following figure:

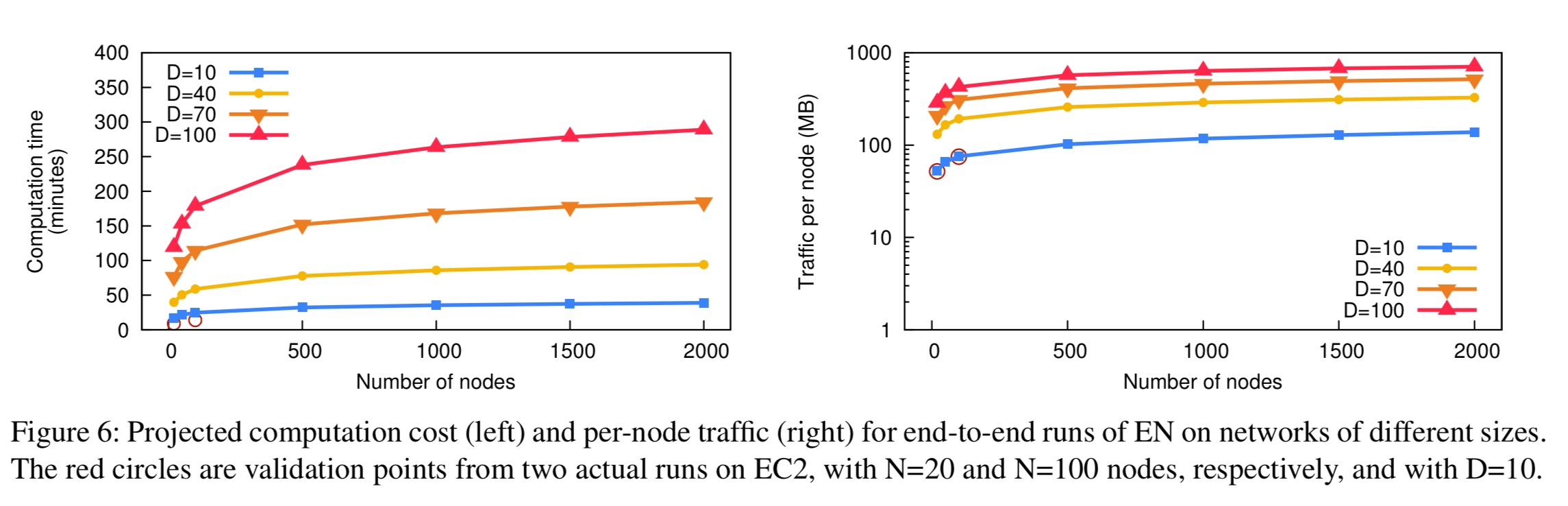
Based on these results, we estimate that an end-to-end run of Eisenberg-Noe for the entire U.S. banking system (N=1,750, D=100) would take 4.8 hours and consume about 750MB of traffic. These costs seem low enough to be practical.

(Without using DStress, and just treating the whole calculation as a large MPC problem, the authors calculate the computation time as about 287 years!).

Section 4.5 of the paper contains an analysis of how frequently this computation can be done such that no adversary can increase their confidence in any fact about the input data by more than a factor of two. The bottom line is that it can be done three times a year:

Since banks must retrospectively disclose their aggregate positions every year anyway, it seems reasonable to replenish the privacy budget once per year. Thus, it seems safe to execute Elliot-Golub-Jackson up to (ln 2) / 0.23, or approximately 3 times per year, which is more frequent than today’s annual stress tests.