Optimizing Distributed Actor Systems for Dynamic Interactive Services – Newell et al. 2016

I’m sure many of you have heard of the Orleans distributed actor system, that was used to build some of the systems supporting Microsoft’s online Halo game.

Halo Presence is an interactive application which implements presence services for a multi-player game running in production on top of Orleans… Orleans makes it easy to scale the system to thousands of games in which millions of players interact in a dynamic way. It instantiates actors on demand, distributing the load across multiple servers transparently to the application… Scaling the Halo Presence service, however, introduces an additional challenge of achieving low latency, because the service is interactive. Remote clients (real players) query the server to find out the status of the other players in the game, and slower response significantly affects user experience.

Orleans has some design features that make it easy to scale out, and to migrate actors transparently from one node to another, but also that lead to higher latencies and lots of serialization and deserialization overhead. Fine-grained and lightweight actors are placed randomly across servers…. “while this policy forgoes the actor locality, it achieves good load balance and throughput scaling.” It’s scalability, but at what cost? ;).

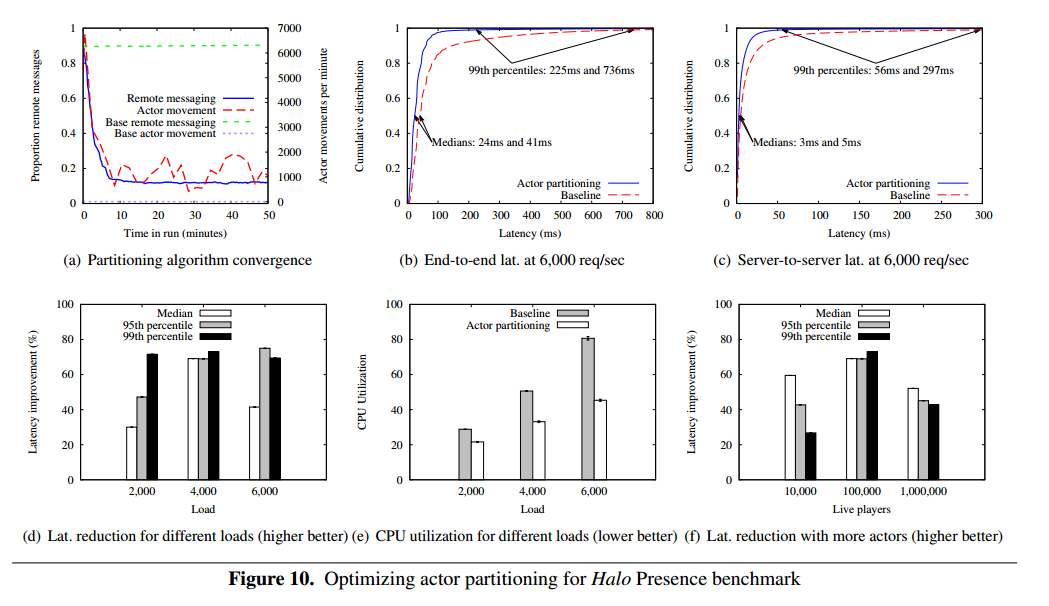
In Halo presence, each player actor sends one message to its game actor that broadcasts it to the 8 players (in the game), who in turn respond back. Thus, each client request results in 18 additional messages sent across the actors. Since Orleans assigns actors to servers at random to avoid hotspots, the vast majority of actor-to-actor interactions cross server boundaries. This is consistent with our finding that ≈ 90% of all messages between actors are remote. Consequently, the number of requests handled by each server is more than an order of magnitude higher than the number of external client requests.

(emphasis mine).

As a consequence, “our measurements show that the original Orleans system fails to satisfy low latency even at moderate scale… such high latency is unacceptable as it gives the perception of a sluggish service.”

What can be done to fix the situation? Two things it turns out (both necessary): firstly we need to introduce dynamic actor placement, so that actors communicating frequently can be migrated to the same servers, all the while preserving overall system balance; and secondly server thread allocation for the SEDA stages within Orleans must also be optimized. The techniques that the authors develop to solve these problems look to be very applicable in other contexts too.

I’m assuming it’s fairly obvious why avoiding lots of fine-grained remote communication might be a good idea. Perhaps the significance of balancing the thread allocations for the stages in a SEDA architecture warrants a little more explanation. Figure 4 (below) shows the average latency a request spends in SEDA stages and queues.

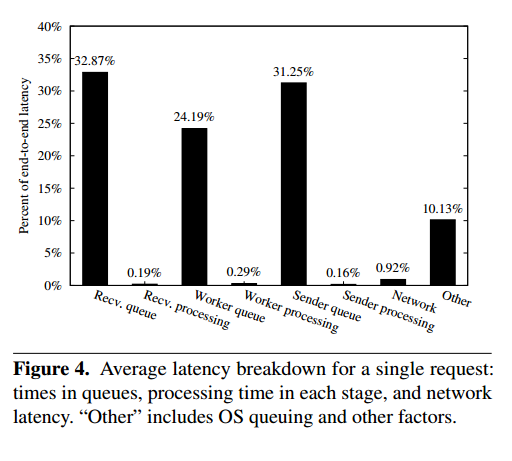
We use the default thread allocation policy in Orleans: a thread per stage per CPU core. We profile a request from the moment it arrives until it leaves the server. Queueing delay dominates the end-to-end latency, and by far exceeds the network latency, as well as the processing time in each stage. This is a symptom of an incorrect allocation of threads across the stages… Thread allocation policy drastically affects the end-to-end latency: the worst performing allocation results in 4x higher latency than the best-performing allocation. Notably, the default configuration used in Orleans is among the worst-performing configurations.

The benefit of co-locating communicating actors on the same server ‘will not materialize if the thread allocation is not dynamically adjusted to the changing server workload.’ Thus,

… dynamically optimizing actor locality and thread allocation together has a greater effect on the end-to-end latency than the effect of each optimization separately… The above analysis leads us to the design of an online optimization framework that constantly monitors server performance and actor communications and quickly adapts to the highly dynamic nature of actor-based applications at scale.

Let’s look in turn at the actor partitioning algorithm, and then the thread allocation optimization, before finishing up by looking at the overall results when the two are put together.

Locality-aware actor partitioning

Consider actors and their communication to form a graph with actors as the vertices, and weighted edges between vertices indicating frequency of communication. What we now have is a balanced graph partitioning problem (known to be NP-hard).

Given n available servers, we seek to partition the graph vertices into n disjoined balanced sets such that the sum of edge weights crossing the partitions is minimized.

The balance criteria is that any for two partitions V_p and V_q, there is less than δ difference between the number of vertices in each of them.

It’s assumed that all actors consume a similar amount of memory and compute resources, and that they have small per-actor state (thus the cost of migration is low). Given that actors are lightweight and fine-grained these simplifying assumptions are reasonable (and borne out by the evaluation).

One way of solving the problem would be to gather all information about the global graph in a central place (single server) and process the resulting huge graph there using GraphChi or similar. Even if you could efficiently collect all the data in one place while accomodating the high rates of graph updates, solving the partitioning problem this way turned out to take several hours – which is no use.

For rapidly time-varying actor graphs, e.g., about 1% of all the edges changing every minute as in the Halo presence example, the messaging and processing overheads of a centralized solution result in an unacceptable delay, making the outcome of the partitioning algorithm likely to be obsolete by the time it finally becomes available.

The authors settled on a distributed partitioning algorithm based on pairwise exchanges of actors. The pairwise protocol is invoked independently and periodically by each server. A server p initiating the protocol proceeds as follows:

• For each remote server q, p calculates a transfer score for each vertex v in p with an edge to one or more vertices in q. This is simply the sum of the weights of all v‘s edges to vertices in q, and represents the expected cost reduction in p from migrating v to q. The total transfer score for q is simply the sum of the transfer scores for all such vertices. Alongside the total transfer score, p also maintains the set of the top k vertices with the highest transfer scores. This is known as the candidate set.
• p then picks the remote server q with the highest total transfer score, and sends an exchange request along with the candidate set S of actors it would like to transfer.
• If q has recently performed an exchange (within the last minute), it rejects the request. In this case p continues to work down its prioritized list of exchange partners until it finds some other partner q prepared to exchange.
• q picks a candidate set T of its own actors which can potentially be transferred to p, in the same way as p picks S. (At this stage, q is still ignoring the potential consequences of taking any of the actors in S from p).
• q constructs two sorted max-heaps, one for S and one for T.
• q begins a greedy iterative process to determine the final subsets S₀ ⊂ S and T₀ ⊂ T that will actually be exchanged:

In each iteration step, q chooses the candidate vertex with the highest transfer score among all vertices. If the vertex migration would violate the balance constraint between q and p, the algorithm chooses the highest-scored vertex from the other heap. The selected vertex v is marked for migration and removed from the respective heap q then updates the scores of all the remaining vertices in both heaps to reflect the migration of v. The algorithm proceeds until both heaps are empty or no more vertices can be moved due to the balancing constraint.

The overall complexity of this approach is ‘practically linear in the number of vertices in the server,’ and the authors show that it converges to a locally optimal partition after finitely many executions.

For efficiency, the implementation doesn’t store weights for every edge, but only the ‘heaviest’ edges – which are determined by the Space-Saving sampling algorithm. Edge statistics are kept locally at each actor, and a global concurrent data structure is periodically updated by traversing all actors from a single thread.

Within 10 minutes of the start of a 100K concurrent player test on a cluster of 10 servers, the proportion of remote actor communications falls to about 12% (vs the 90% baseline with the random placement policy). Locality aware actor partitioning reduces the 99th percentile latency by more than 3x, with gains more significant as loads increase. CPU utilization per server is reduced by 25% at lower system load, and 45% at higher load due to the reduction in serialization overheads.

(click for larger view).

Latency-optimized thread allocation

Previous work on SEDA-based servers introduced a queueing-theoretc model of the system. However, we are not aware of any work that directly uses a latency-related formulation to optimize thread allocation.

The traditional approach of allocating more threads to stages with long queues is prone to allocation fluctuations since queue-lengths respond in an extremely non-linear fashion to addition of capacity via threads, depending on how close the load is to the capacity.

The main problem is that even with minor (+/- 1) fluctuations in the thread allocation, the service latency may increase dramatically… this behaviour can be intuitively explained using queueing theory. In the M/M/1 queue model, the average queue length is ρ/(1-ρ). ρ is defined as the arrival rate divided by the service rate, and represents the proportion of available resources that a stage has. When ρ is small (service rate is high, many free threads), differences in ρ do not affect the average queue length much: the queue is almost empty. Only when ρ approaches 1.0 (arrival rate approaches service rate, not enough threads), the queue length grows dramatically. The function ρ/(1-ρ) is nonlinear in ρ (hence nonlinear in the number of threads), and becomes steeper as ρ approaches one.

Instead of using queue lengths therefore, the authors define a latency minimization problem parameterized by actual system parameters measured at runtime. The solution simultaneously determines the thread allocation for all stages, and hence is less prone to allocation fluctations.

For each queue/stage the M/M/1 latency function 1/(μ_i – λ_i) is used where μ_i is the service rate of the queue i, and λ_i is the arrival rate. The weighted average of this per-queue latency across all queues is used as a proxy for the end-to-end latency. Multi-threading overheads (context switching) are addressed by adding a regularization parameter that promotes solutions that favor fewer threads. Under the constraints that each stage must service events at least as fast as they arrive, and that the available resources at the server are not exceeded, the minimization problem yields a closed form solution:

where t_i is the number of threads to be allocated at stage i and s_i is the service rate per thread at stage i. See the full paper for details and an explanation of how the necessary parameters can be estimated from the running system.

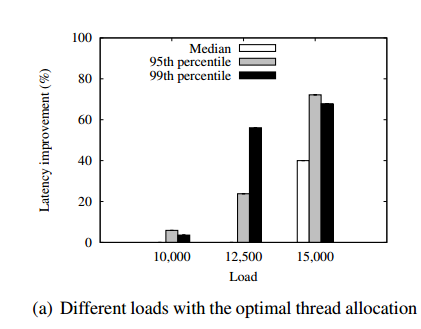
Using this scheme, the authors observe significant latency reduction, in particular for heavy loads.

For example, the latency of the optimized configuration under the highest load of 15K requests/second is reduced by 68% in the 99th percentile, and by 58% in the median.

Putting them together

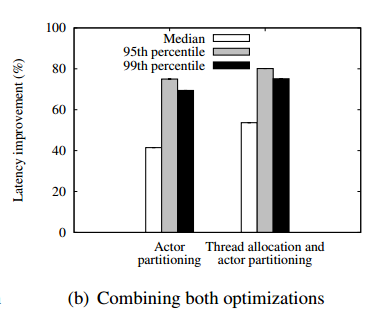
The optimized actor partitioning is the primary factor contributing to the latency improvement. Yet, combining both optimizations yields additional latency savings as shown in Figure 11(b): Optimizing the thread allocation provides additional reduction of 21% in the median latency, and 9% in the 99th percentile latency. In total, ActOp reduces the median latency by 55% and the 99th percentile by 75% over the baseline configuration.

We believe that the principles and techniques we develop in ActOp are general and can be applied to other distributed actor systems. For example, our techniques can be applied to similar challenges of cross-server communication and sub-optimal threads allocation in Akka and Erlang. However, in these systems the runtime cannot automatically and transparently move actors, making it the application’s responsibility to adjust actors placement. In contrast, the virtual nature of actors in Orleans enables dynamic actor migration, which allows the optimizations in ActOp to be integrated in the system runtime. Further, our thread allocation mechanism may be applicable to other SEDA-like systems that maintain
multiple thread pools.