GloVe: Global Vectors for Word Representation – Pennington et al. 2014
Yesterday we looked at some of the amazing properties of word vectors with word2vec. Pennington et al. argue that the online scanning approach used by word2vec is suboptimal since it doesn’t fully exploit statistical information regarding word co-occurrences. They demonstrate a Global Vectors (GloVe) model which combines the benefits of the word2vec skip-gram model when it comes to word analogy tasks, with the benefits of matrix factorization methods that can exploit global statistical information. The GloVe model…
… produces a vector space with meaningful substructure, as evidenced by its performance of 75% on a recent word analogy task. It also outperforms related models on similarity tasks and named entity recognition.
The source code for the model, as well as trained word vectors can be found at http://nlp.stanford.edu/projects/glove/
Matrix factorization vs shallow-window methods
Matrix factorization methods such as Latent Semantic Analysis (LSA) use low-rank approximations to decompose large matrices capturing statistical information about a corpus. In LSA, rows correspond to words or terms, and the columns correspond to different documents in the corpus. In the Hyperspace Analogue to Language (HAL) and derivative approaches, square matrices are used where the rows and columns both correspond to words and the entries correspond to the number of times a given word occurs in the context of another given word (a co-occurrence matrix). One problem that has to be overcome here is that frequent words contribute a disproportionate amount to the similarity measure and so some kind of normalization is needed.
Shallow-window methods learn word representations from local context windows (as we saw yesterday with word2vec):
Unlike the matrix factorization methods, the shallow window-based methods suffer from the disadvantage that they do not operate directly on the co-occurrence statistics of the corpus. Instead, these models scan context windows across the entire corpus, which fails to take advantage of the vast amount of repetition in the data.
How GloVe finds meaning in statistics
The statistics of word occurrences in a corpus is the primary source of information available to all unsupervised methods for learning word representations, and although many such methods now exist, the question still remains as to how meaning is generated from these statistics, and how the resulting word vectors might represent that meaning.
Pennington et al. present a simple example based on the words ice and steam that sheds some light on this question.
The relationship of these words can be examined by studying the ratio of their co-occurrence probabilities with various probe words, k.
Let P(k|w) be the probability that the word k appears in the context of word w. Consider a word strongly related to ice, but not to steam, such as solid. P(solid | ice) will be relatively high, and P(solid | steam) will be relatively low. Thus the ratio of P(solid | ice) / P(solid | steam) will be large. If we take a word such as gas that is related to steam but not to ice, the ratio of P(gas | ice) / P(gas | steam) will instead be small. For a word related to both ice and steam, such as water we expect the ratio to be close to one. We would also expect a ratio close to one for words related to neither ice nor steam, such as fashion.
The following table shows that this does indeed pan out in practice:
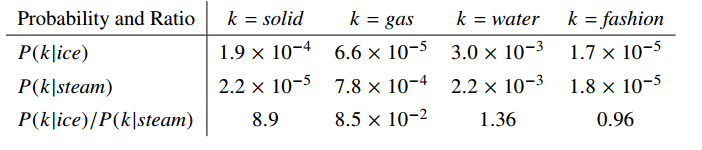
The above argument suggests that the appropriate starting point for word vector learning should be with ratios of co-occurrence probabilities rather than the probabilities themselves…. Since vector spaces are inherently linear structures, the most natural way to [encode the information present in a ratio in the word vector space] is with vector differences.
From the GloVe project page:
The training objective of GloVe is to learn word vectors such that their dot product equals the logarithm of the words’ probability of co-occurrence. Owing to the fact that the logarithm of a ratio equals the difference of logarithms, this objective associates (the logarithm of) ratios of co-occurrence probabilities with vector differences in the word vector space. Because these ratios can encode some form of meaning, this information gets encoded as vector differences as well. For this reason, the resulting word vectors perform very well on word analogy tasks, such as those examined in the word2vec package.
To deal with co-occurrences that happen rarely or never – which are noisy and carry less information than the more frequent ones – the authors use a weighted least squares regression model. One class of weighting functions found to work well can be parameterized as
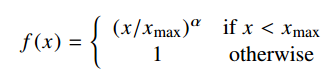
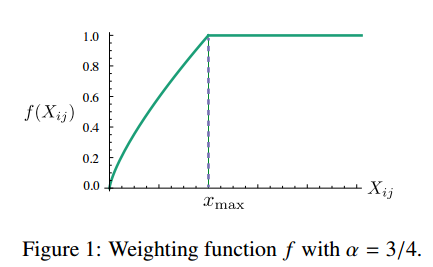
The performance of the model depends weakly on the cutoff, which we fix to xmax = 100 for all our experiments. We found that α = 3/4 gives a modest improvement over a linear version with α = 1. Although we offer only empirical motivation for choosing the value 3/4, it is interesting that a similar fractional power scaling was found to give the best performance in [word2vec].
The model generates two sets of word vectors. When the co-occurrence matrix is symmetric, these differ only as a result of their random initializations: the two sets of vectors should perform equivalently.
On the other hand, there is evidence that for certain types of neural networks, training multiple instances of the network and then combining the results can help reduce overfitting and noise and generally improve results. With this in mind, we choose to use the sum [of the two sets] as our word vectors. Doing so typically gives a small boost in performance, with the biggest increase in the semantic analogy task.
Results
The model was trained on five corpora including a 2010 Wikipedia dump with 1 billion tokens and a 2014 Wikipedia dump with 1.6 billion tokens, Gigaword 5 with 4.3 billion tokens, a combination of Gigaword 5 and the 2014 Wikipedia dump totalling 6 billion tokens, and finally 42 billion tokens of web data from Common Crawl.
We tokenize and lowercase each corpus with the Stanford tokenizer, build a vocabulary of the 400,000 most frequent words, and then construct a matrix of co-occurence counts… we use a decreasing weighting function so that word pairs that are d words apart contribute 1/d to the total count.
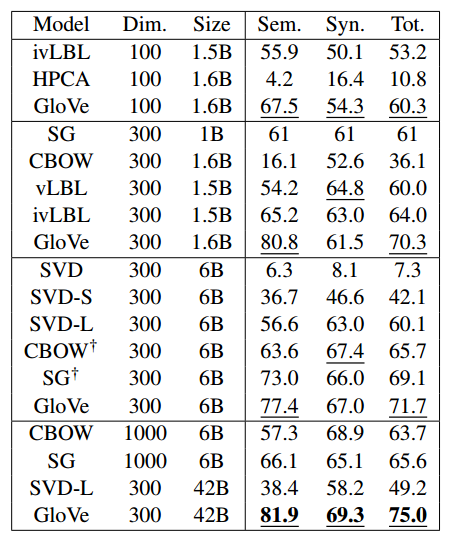
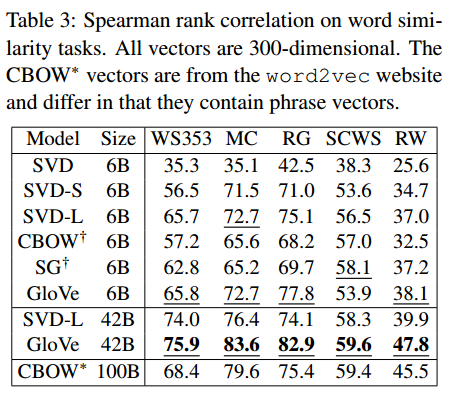
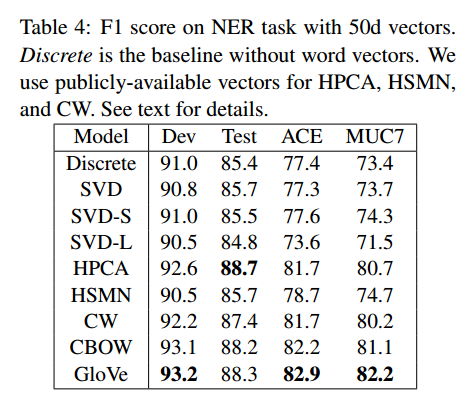
This pass can be computationally expensive, but it’s a one time up-front cost. GloVe does very well on the word analogy task, achieving class-leading combined accuracy of 75%. It also gets great results on word similarity and named entity recognition tests.
Word analogy task results:
Word similarity:
Named Entity Recognition:
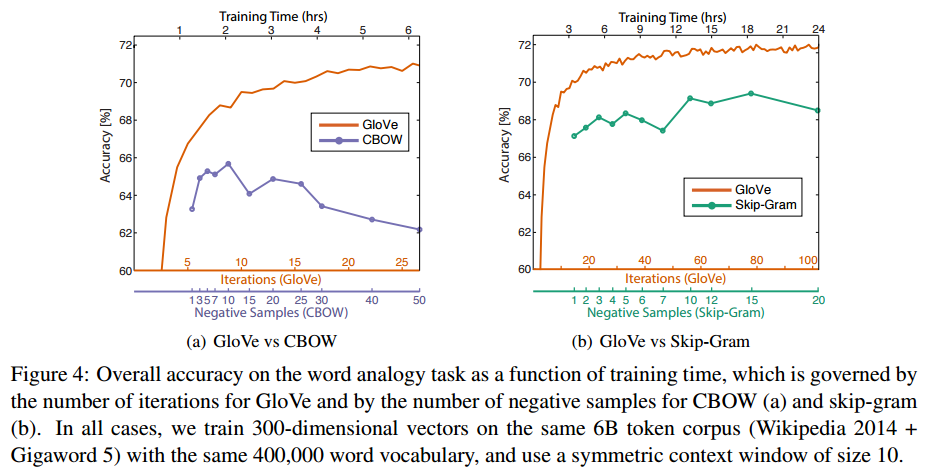
Compared to word2vec, for the same amount of training time GloVe shows improved accuracy on the word analogy task.
The authors conclude:
In this work we argue that the two classes of methods are not dramatically different at a fundamental level since they both probe the underlying co-occurrence statistics of the corpus, but the efficiency with which the count-based methods capture global statistics can be advantageous. We construct a model that utilizes this main benefit of count data while simultaneously capturing the meaningful linear substructures prevalent in recent log-bilinear prediction-based methods like word2vec. The result, GloVe, is a new global log-bilinear regression model for the unsupervised learning of word representations that outperforms other models on word analogy, word similarity, and named entity recognition tasks.