Mergeable replicated data types

Mergeable replicated data types Kaki et al., OOPSLA’19

This paper was published at OOPSLA, but perhaps it’s amongst the distributed systems community that I expect there to be the greatest interest. Mergeable Replicated Data Types (MRDTs) are in the same spirit as CRDTs but with the very interesting property that they compose. Furthermore, a principled approach for deriving MRDTs is provided, allowing a wide range of data-types to be lifted to their mergeable, replicated counterparts with very little effort on the part of the programmer. The paper sets the discussion in the context of geo-replicated distributed systems, but of course the same mechanisms could be equally useful in the context of local-first applications.

There’s a lot of material in this paper’s 29 pages, and to make sure I have the space to properly understand the ideas (the process of summary writing is a critical part of that for me), I’m going to spread my coverage over two posts.

We’ll begin by looking at the context and the high-level idea behind MRDTs, then we’ll investigate how merge specifications can be derived and composed, and how merge implementations can be derived too. Finally we’ll touch on the implementation of MRDTs in Quark, an end-to-end OCaml-based system for the creation of applications with mergeable, distributable state.

Local operation, global coordination

To ensure low-latency and high availability (or even just the ability to work when offline) we want to be able to operate locally and independently on data types. To support cross-device and cross-cloud use cases we want to be able to synchronise local changes in a way that results in a consistent global state.

The authors catalogue three basic approaches to meeting these goals:

Engineering algorithms to be cognisant of replicated behaviour, which leads us to replicated data types, “applications that expose the same interface as ordinary (sequential) data types, but whose implementations are aware of replicated state.“
Using concurrent revision strategies that directly expose client operations to create and synchronise version of object state
A specification-first approach to characterising what application correctness means in the presence of replication, and then using the specs to guide implementation strategy.

In all three cases, developers must grapple with various operational nuances of replication, either in the way objects are defined, abstractions used, or specifications written.

MRDTs combine elements of all three strategies. As the name suggests, the abstraction exposed to the programmer is of a replicated data type. Under the covers they use versioned states and explicit merging operations, and they guide this process through invertible relational specifications.

The invertible relational specifications are at the heart of MRDTs. By defining a mapping from the domain of a data type to relational sets (and back again), we can reason about merge semantics in the relational set domain. Give a version tree, the core merge operation is a three-way merge taking as input two concurrently modified versions to be merged, and their lowest common ancestor (LCA) in the version tree.

…our focus in this paper is on deriving such correct merge functions automatically over arbitrarily complex (i.e., composable) data type definitions, and in the process, ascribe to them a meaningful and useful distributed semantics.

Let’s start with a very simple counter example and build up from there. Consider a Counter data type supporting not only add and subtract operations, but also multiply and divide. The immediate issue facing us is that multiplication operations do not commute with addition and subtraction. E.g., (+2), (x5) != (x5), (+2). We could globally synchronise state every time we want to do a multiplication, but that’s going to be expensive and have availability implications.

Under such circumstances, it is not readily apparent if we can define replicated counters that support multiplication and yet still have a well-defined semantics that guarantees all replicas will converge to the same counter state. Fortunately, a state- and merge-centric view of replication lets us arrive at such a semantics naturally…

Here’s a revision history in which we start at the state ‘5’, and then two concurrent branches apply the ‘-1’ and ‘x2’ operations respectively. When we come to merge the states we have ‘10’, ‘4’ and the state of the lowest common ancestor: ‘5’.

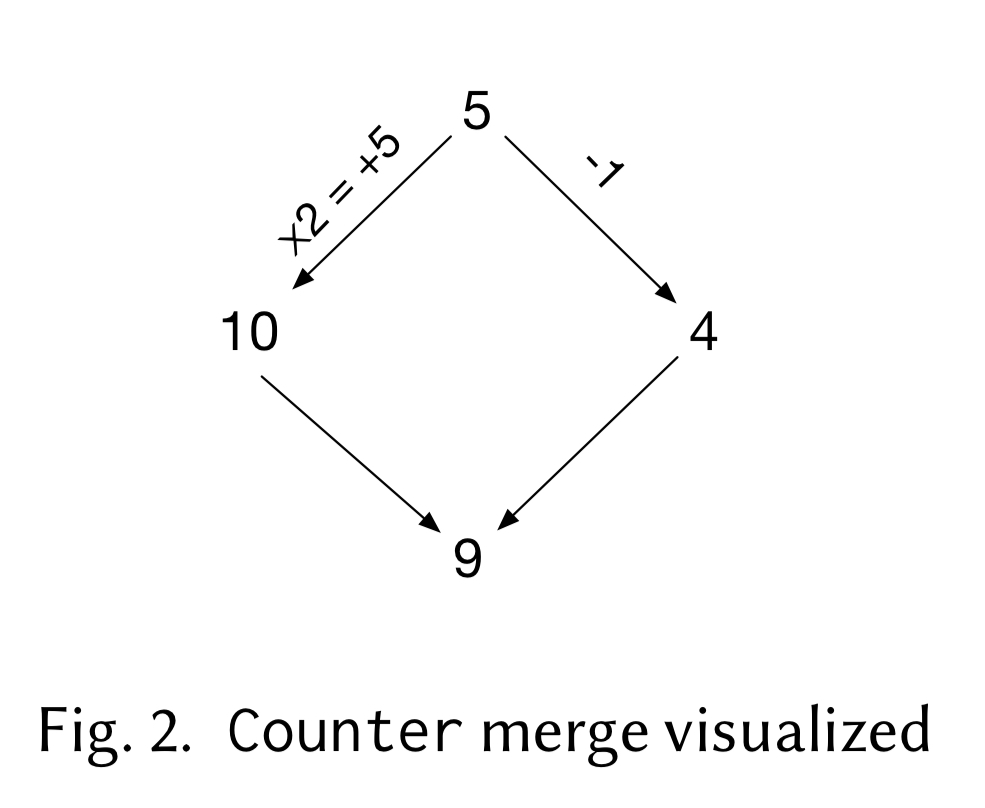
The proposal in this case is that the result of the merge operation be 9. Merging versions $v1$ and $v2$ with a lowest common ancestor $l$ , the three-way merge function is defined as:

[code lang=ocaml]
let merge l v1 v2 = l + (v1 - l) + (v2 -l)
[/code]

I.e., we compose (add) the differences between the two versions and their LCA. So we have (+5) and (-1), which combined give +4, and when added to the LCA value 5 yields 9.

These rules do not guarantee linearizability (e.g. consider the case when the concurrent operations are ‘x2’ and ‘x3’), but they do guarantee convergence. In some applications they may even be useful! The example given is a banking application which uses the multiplication operation to compute interest on an account.

While this concrete example shows the principle of a three-way merge, it’s not yet a process we can generalise. That’s where those invertible relational specifications come in. Such a specification consists of a abstraction function that maps the values of a type to the relational domain, and a concretization function that maps back again.

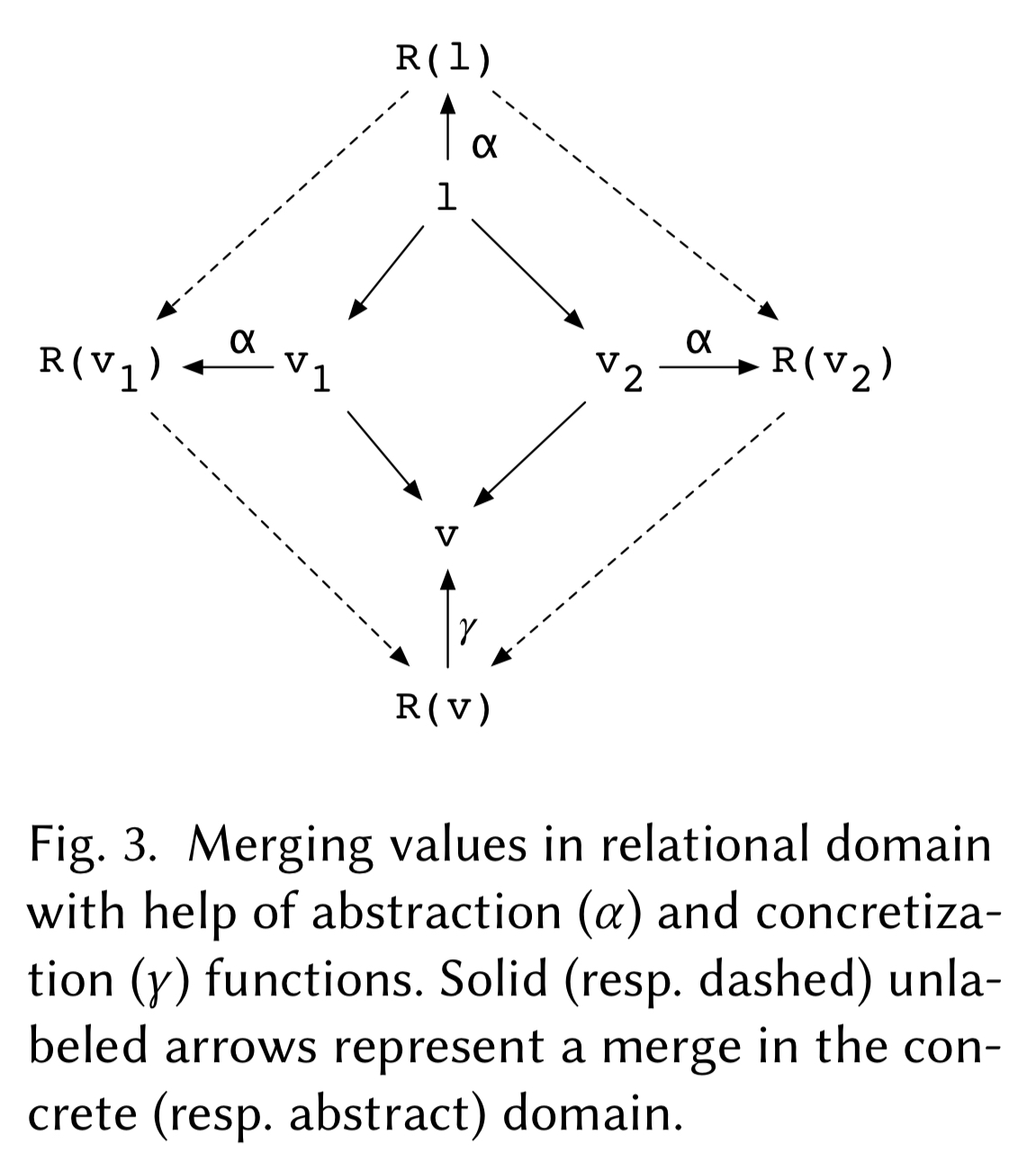
(In mathematical terms, this is called a bijection.)

The semantics of a merge in the relational set domain, albeit non-trivial, is nonetheless standard in the sense that it is independent of the concrete interpretations (in the data type domain) of the merging relations, and hence can be defined once and for all.

A queue example

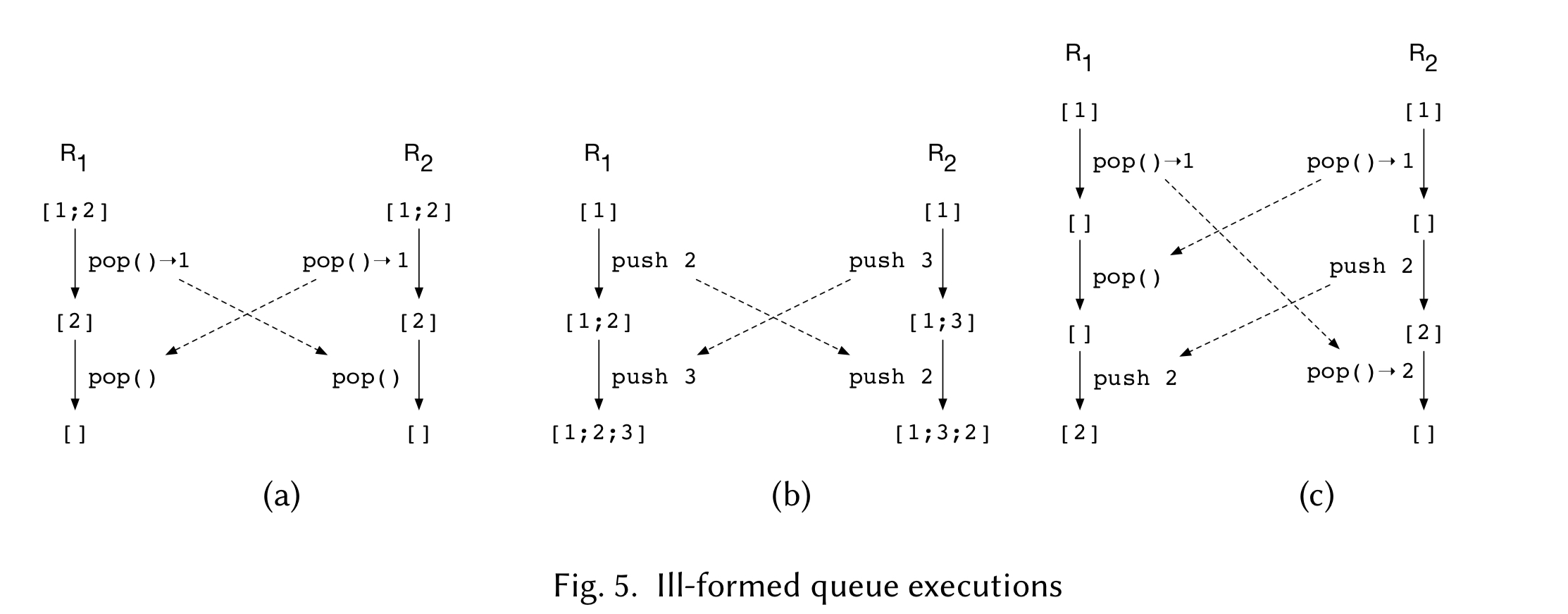
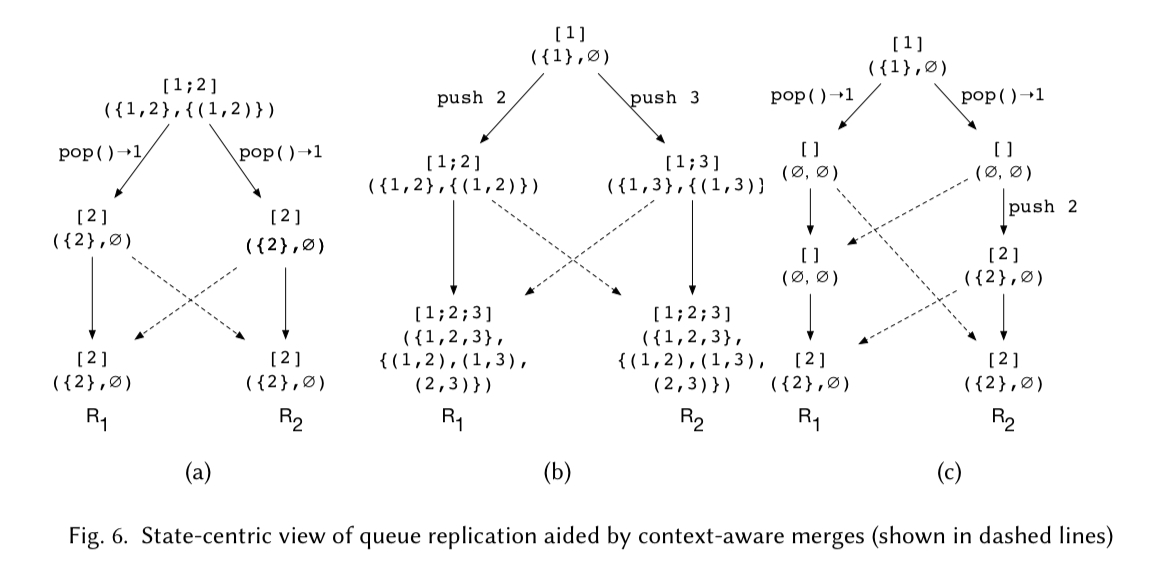
The motivating example to explore this idea is a queue. Consider a queue with push and pop operations, where the state is an ordered list of integer values. If we start off with queue state [1;2] then there are lots of ways we can get into trouble with concurrent pushes and pops! The following figure illustrates three of them.

Consider a lowest common ancestor state of the queue $l$ (e.g. [1;2] in the preceding example), and two concurrent versions $v1$ and $v2$ to be merged, what properties should hold between $l$ , $v1$ , and $v2$ and the resulting merge state $v$ ?

A queue element that was never consumed (i.e. was not popped in either version) should still be present in $v$ .
For every $x$ in $l$ , if $x$ is popped in either $v1$ or $v2$ then it should not be present in $v$ . (The assumption here is that two entries with the same numeric value are distinct elements.)
If $x$ is not in $l$ and it is newly pushed into (i.e., present in) $v1$ or $v2$ then it should be in $v$ .
Partial ordering is preserved: for every $x$ and $y$ in $l$ (or $v1$ , or $v2$ ) then if $x$ and $y$ are not deleted then $x$ also occurs before $y$ in $v$ .With these rules in mind we can map queue state to relations using a pair of relations: $R_{mem}$ is a set containing all the members of a queue, and $R_{ob}$ is an occurs-before relation relating every pair of elements $x$ and $y$ in the queue such that if $x$ occurs before $y$ in the queue, then $(x, y) \in R_{ob}$ .

Now that we know how to map queues to the relational domain, we can define the three-way merge operation in that domain as:

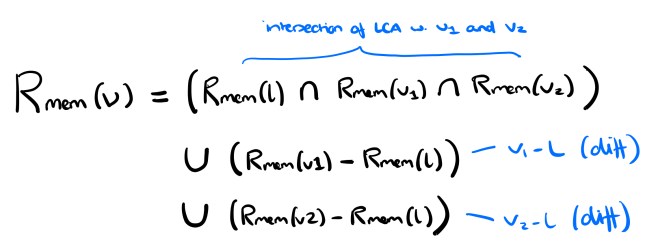
and

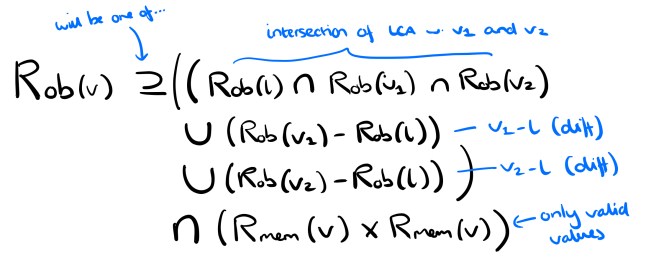
Note that the merge specification for the observe-before relation is under-specified, i.e. it accommodates multiple possible resulting orderings so long as the given ordering constraints are satisfied. That’s going to give us problems with convergence. We can eliminate the non-determinism by defining a consistent ordering relation among elements coming from different queues (an arbitration function): for example, lexicographic order.

After merging state in the relational domain according to these rules, we can project it back into the queue domain.

If we take these rules and replay the three failing queue scenarios from earlier, we can see that our queue now arrives at a consistent global state in all of them:

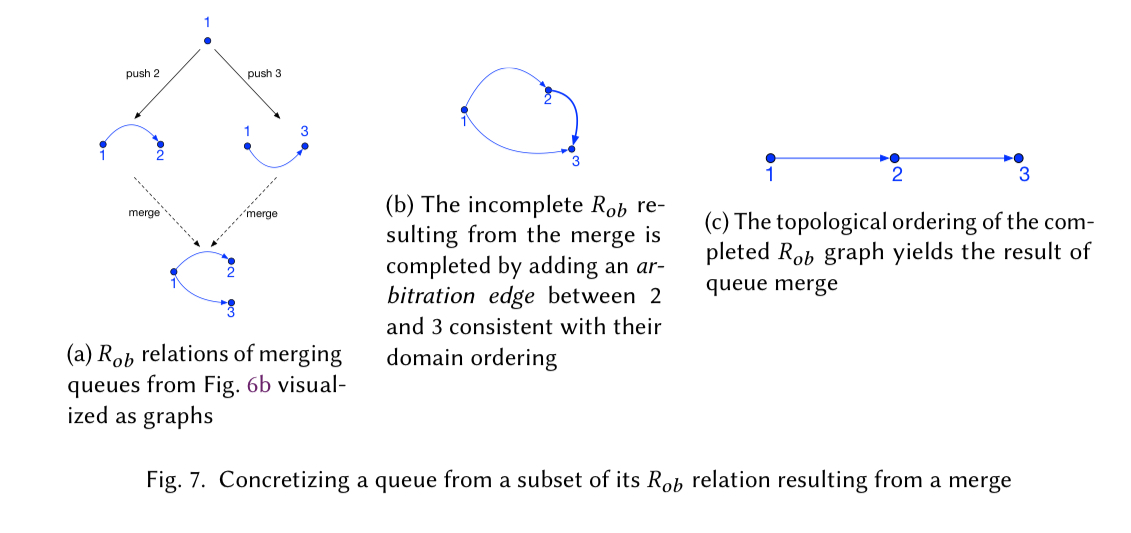
One implementation strategy to materialise the queue state from the pair of relations $R_{mem}$ and $R_{ob}$ is to construct a directed graph with vertices $R_{mem}(v)$ and edges $R_{ob}(v)$ , and ties broken with additional arbitration edges. A topological ordering of the graph then yields the queue.

We have generalized the aforementioned graph-based approach for concretizing ordering relations, and abstracted it away as a library function $\gamma_{ord}$ . Give ord, an arbitration order the function $\gamma_{ord}$ concretizes an ordering relation of a data structure (not necessarily a total order) as a graph isomporphic to that structure, using the abritration order to break ties…

The general case

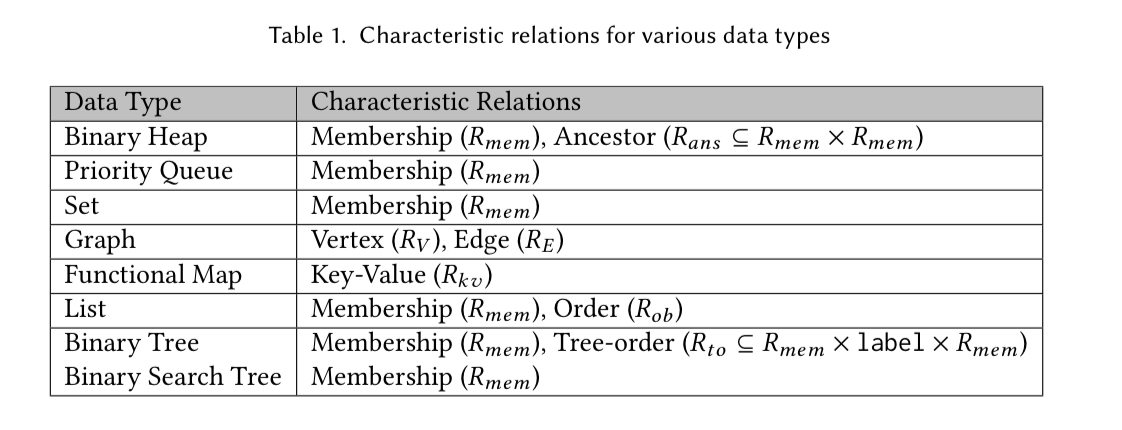
We’re getting closer to the generalised MRDT approach now. For each data type (e.g., list and queue as we’ve seen so far), we can define characteristic relations that define the representation in the relational domain (e.g., $R_{mem}$ and $R_{ob}$ for the queue example). The characteristic relations for a range of data types are shown in the table below.

Next time out we’ll see how to automatically derive the merge specification for an MRDT given the characteristic relations and the abstraction/concretisation functions.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic

Mergeable replicated data types – Part I

Local operation, global coordination