Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead Rudin et al., arXiv 2019
With thanks to Glyn Normington for pointing out this paper to me.
It’s pretty clear from the title alone what Cynthia Rudin would like us to do! The paper is a mix of technical and philosophical arguments and comes with two main takeaways for me: firstly, a sharpening of my understanding of the difference between explainability and interpretability, and why the former may be problematic; and secondly some great pointers to techniques for creating truly interpretable models.
There has been a increasing trend in healthcare and criminal justice to leverage machine learning (ML) for high-stakes prediction applications that deeply impact human lives… The lack of transparency and accountability of predictive models can have (and has already had) severe consequences…
Defining terms
A model can be a black box for one of two reasons: (a) the function that the model computes is far too complicated for any human to comprehend, or (b) the model may in actual fact be simple, but its details are proprietary and not available for inspection.
In explainable ML we make predictions using a complicated black box model (e.g., a DNN), and use a second (posthoc) model created to explain what the first model is doing. A classic example here is LIME, which explores a local area of a complex model to uncover decision boundaries.
An interpretable model is a model used for predictions, that can itself be directly inspected and interpreted by human experts.
Interpretability is a domain-specific notion, so there cannot be an all-purpose definition. Usually, however, an interpretable machine learning model is constrained in model form so that it is either useful to someone, or obeys structural knowledge of the domain, such as monotonicity, or physical constraints that come from domain knowledge.
Explanations don’t really explain
There has been a lot of research into producing explanations for the outputs of black box models. Rudin thinks this approach is fundamentally flawed. At the root of her argument is the observation that ad-hoc explanations are only really “guessing” (my choice of word) at what the black box model is doing:
Explanations must be wrong. They cannot have perfect fidelity with respect to the original model. If the explanation was completely faithful to what the original model computes, the explanation would equal the original model, and one would not need the original model in the first place, only the explanation.
Even the word “explanation” is problematic, because we’re not really describing what the original model actually does. The example of COMPAS (Correctional Offender Management Profiling for Alternative Sanctions) brings this distinction to life. An linear explanation model for COMPAS created by ProPublica, and dependent on race, was used to accuse COMPAS (which is a black box) of depending on race. But we don’t know whether or not COMPAS has race as a feature (though it may well have correlated variables).
Let us stop calling approximations to black box model predictions explanations. For a model that does not use race explicitly, an automated explanation “This model predicts you will be arrested because you are black” is not a model of what the model is actually doing, and would be confusing to a judge, lawyer or defendant.
In the image space, saliency maps show us where the network is looking, but even they don’t tell us what it is truly looking at. Saliency maps for many different classes can be very similar. In the example below, the saliency based ‘explanations’ for why the model thinks the image is husky, and why it thinks it is a flute, look very similar!

Since explanations aren’t really explaining, identifying and troubleshooting issues with black box models can be very difficult
Arguments against interpretable models
Given the issues with black-box models + explanations, why are black-box models so in-vogue? It’s hard to argue against the tremendous recent successes of deep learning models, but we shouldn’t conclude from this that more complex models are always better.
There is a widespread belief that more complex models are more accurate, meaning that a complicated black box is necessary for top predictive performance. However, this is often not true, particularly when the data is structured, with a good representation in terms of naturally meaningful features.
As a consequence of the belief that complex is good, it’s also a commonly held myth that if you want good performance you have to sacrifice interpretability:
The belief that there is always a trade-off between accuracy and interpretability has led many researchers to forgo the attempt to produce an interpretable model. This problem is compounded by the fact that researchers are now trained in deep learning, but not in interpretable machine learning…
The Rashomon set says that we are often likely to be able to find an interpretable model if we try: given that the data permit a large set of reasonably accurate predictive models to exist, it often contains at least one model that is interpretable.
This suggests to me an interesting approach of first doing the comparatively quicker thing of trying a deep learning method without any feature engineering etc.. If that produces reasonable results, we know that the data permits the existing of reasonably accurate predictive models, and we can invest the time in trying to find an interpretable one.
For data that are unconfounded, complete, and clean, it is much easier to use a black box machine learning method than to troubleshoot and solve computationally hard problems. However, for high-stakes decisions, analyst time and computational time are less expensive than the cost of having a flawed or overly complicated model.
Creating interpretable models
Section 5 in the paper discusses three common challenges that often arise in the search for interpretable machine learning models: constructing optimal logical models, constructing optimal (sparse) scoring systems, and defining what interpretability might mean in specific domains.
Logical models
A logical model is just a bunch of if-then-else statements! These have been crafted by hand for a long time. The ideal logical model would have the smallest number of branches possible for a given level of accuracy. CORELS is a machine learning system designed to find such optimal logical models. Here’s an example output model that has similar accuracy to the blackbox COMPAS model on data from Broward County, Florida:

Note that the figure caption calls it a ‘machine learning model.’ That terminology doesn’t seem right to me. It’s a machine-learned-model, and CORELS is a machine learning model that produces it, but the IF-THEN-ELSE statement is not itself a machine learning model. Nevertheless, CORELS looks very interesting and we’re going to take a deeper look at it in the next edition of The Morning Paper.
Scoring systems
Scoring systems are used pervasively through medicine. We’re interested in optimal scoring systems that are the outputs of machine learning models, but look like they could have been produced by a human. For example:
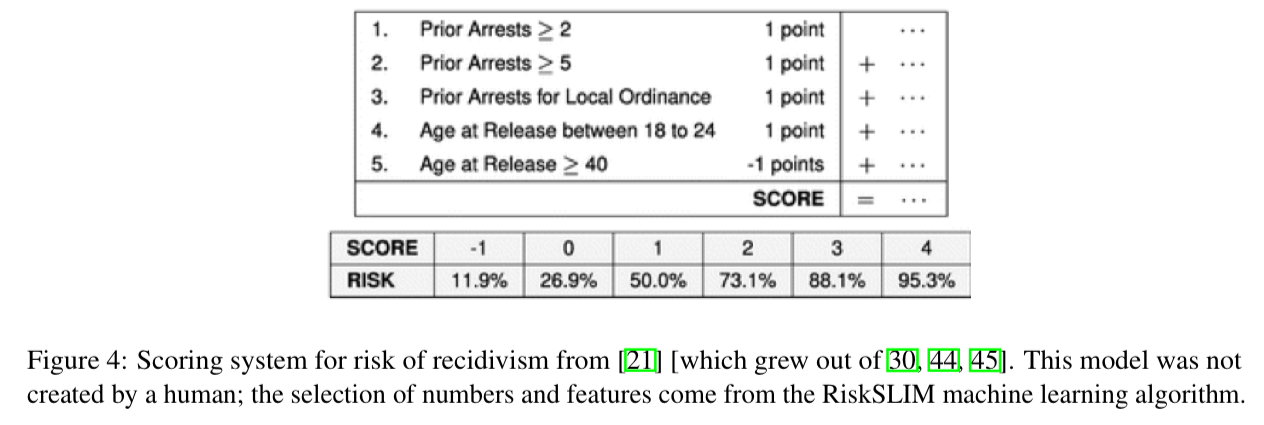
This model was in fact produced by RiskSLIM, the Risk-Supersparse-Linear-Integer-Models algorithm (which we’ll also look at in more depth later this week).
For both the CORELS and the RiskSLIM models, the key thing to remember is that although they look simple and highly interpretable, they give results with highly competitive accuracy. It’s not easy getting things to look this simple! I certainly know which models I’d rather deploy and troubleshoot given the option.
Designing for interpretability in specific domains
…even for classic domains of machine learning, where latent representations of data need to be constructed, there could exist interpretable models that are as accurate as black box models.
The key is to consider interpretability in the model design itself. Fore example, if an expert where to explain to you why they classified an image in the way that they did, they would probably point out different parts of the image that were important in their reasoning process (a bit like saliency), and explain why. Bringing this idea to network design, Chen, Li, et al. build a model that during training learns parts of images that act as prototypes for a class, and then during testing finds parts of the test image similar to the prototypes it has learned.
These explanations are the actual computations of the model, and these are not posthoc explanations. The network is called “This look like that” because its reasoning process considers whether “this” part of the image looks like “that” prototype.

Explanation, Interpretation, and Policy
Section 4 of the paper discusses potential policy changes to encourage interpretable models to be preferred (or even required in high-stakes situations).
Let us consider a possible mandate that, for certain high-stakes decisions, no black box should be deployed when there exists an interpretable model with the same level of performance.
That sounds a worthy goal, but as worded it would be very tough to prove that there doesn’t exist an interpretable model. So perhaps companies would have to be required to be able to produce evidence of having searched for an interpretable model with an appropriate level of diligence…
Consider a second proposal, which is weaker than the one provided above, but which might have a similar effect. Let us consider the possibility that organizations that introduce black box models would be mandated to report the accuracy of interpretable modeling methods.
If this process is followed, we’re likely to see a lot fewer black box machine learning models deployed in the wild if the author’s experience is anything to go by:
It could be possible that there are application domains where a complete black box is required for a high stakes decision. As of yet, I have not encountered such an application, despite having worked on numerous applications in healthcare and criminal justice, energy reliability, and financial risk assessment.
The last word
If this commentary can shift the focus even slightly from the basic assumption underlying most work in Explainable ML— which is that a black box is necessary for accurate predictions— we will have considered this document a success…. If we do not succeed [in making policy makers aware of the current challenges in interpretable machine learning], it is possible that black box models will continue to be permitted when it is not safe to use them.
Thanks! Alas, I think what’s missing is the “why” and “other variables” of interability.
Consider a law enforcement officer whose intuition is not to arrest a teenager. Is she being naive? Wishful thinking? Or is there another factor that the model isn’t considering (e.g. strong family or community support? Strong desire to succeed? Etc)
Really enjoyed this article. Thanks for writing it!
Minor typos: “Fore example, if an expert where to explain to you…”