Distributed consensus revised Howard, PhD thesis
Welcome back to a new term of The Morning Paper! To kick things off, I’m going to start by taking a look at Dr Howard’s PhD thesis, ‘Distributed consensus revised’. This is obviously longer than a standard paper, so we’ll break things down over a few days. As the title suggests, the topic in hand is distributed consensus:
Single-valued agreement is often overlooked in the literature as already solved or trivial and is seldom considered at length, despite being a vital component in distributed systems which is infamously poorly understood… we undertake an extensive examination of how to achieve consensus over a single value.
What makes this much harder than it might at first appear of course, is the possibility of failures and asynchronous communication. In the face of this, an algorithm for consensus must meet three safety requirements and two progress requirements:
- Non-triviality: the decided value must have been proposed by a participant (so for example, solutions which always choose a fixed pre-determined value are not acceptable)
- Safety: if a value has been decided, no other value will be decided
- Safe learning: if a participant learns a value, it must learn the decided value
- Progress: under a specified set of liveness conditions, if a value has been proposed by a participant then a value is eventually decided
- Eventual learning under a specified set of liveness conditions, if a value has been decided then a value is eventually learned
The first part of the thesis examines the Paxos family of algorithms, and is a great resource for navigating this complex space. A combination of 16 different lemma and theorems are used to prove that Paxos does provide the desired safety and progress guarantees. The proofs are carefully tied back to 10 different properties of the classic Paxos algorithm.
The surprising results of this approach are twofold: firstly, the proof of correctness did not use the full strength of the properties provided and secondly, there are many approaches which satisfy the same properties.
The second part of the thesis uses these insights to generalise Paxos, weakening the requirements for quorum intersection, phase completion, value selection, and epoch allocation. It helps us to tease apart what is essential to the problem of distributed consensus , and what is merely a design choice of a particular solution. The solution space that is opened up offers greater flexibility in performance and reliability trade-offs, new progress guarantees, and improved performance.
These are important results since as well as being notoriously difficult to understand and to implement, Paxos has some well-known and not-so-well-known limitations:
The reliance on majority agreement means that the Paxos algorithm is slow to reach decisions… systems are limited in scale, often to three or five participants, as each additional participant substantially decreases overall performance. It is widely understood that Paxos is unable to reach an agreement if the majority of participants have failed. However, this is only part of the overall picture, failure to reach agreement can result not only from unavailable hosts but also network partitions, slow hosts, network congestion, contention for resources such as persistent storage, clock skew, packet loss and countless other scenarios. Such issues are commonplace in some systems…
Let’s begin our journey by considering one of the simplest solutions possible…
The single acceptor algorithm
We’ll distinguish between two different roles in the system: proposers propose values that they wish to have chosen, and acceptors agree and persist decided values. For all the scenarios we’ll be considering, the set of acceptors and proposers is fixed and known in advance.
A consensus algorithm defines the process by which a value v is chosen by the acceptors from the proposers. We refer to the point in time when the acceptors have committed to a particular value as the commit point.
The single acceptor algorithm is the simplest non-trivial consensus algorithm you can imagine. We have n proposers but only one acceptor. The acceptor chooses the first value proposed to it.

Proposers propose a value, and learn the decided value by return:

If you check this off against the safety and progress requirements we looked at earlier, you’ll see that it meets all of them. The single acceptor provides total ordering. This advantage is also its weakness though: if the acceptor fails the algorithm cannot make progress until it recovers. Removing that single point of failure and supporting multiple acceptors leads us to Paxos…
Classic Paxos
Unoptimised classic Paxos can reach agreement with two round trips to the majority of acceptors, and three synchronous writes to persistent storage. It requires that a majority of acceptors and at least one proposer be up and communicating synchronously for liveness. The algorithm has two phases: a learning phase where proposers learn about the current state of the system, and a deciding (writing) phase when a value is chosen. Central to the algorithm is the idea of an epoch (aka view number, round number, instance value or ballot number): an epoch is a member of an infinite totally ordered set, such as the integers. A proposal is an epoch and value pair.
In phase one proposers send prepare messages with an epoch number, and acceptors send back promises. Based on the information they learned in phase one, in phase two proposers may propose a value for an epoch, and acceptors send back accept messages.
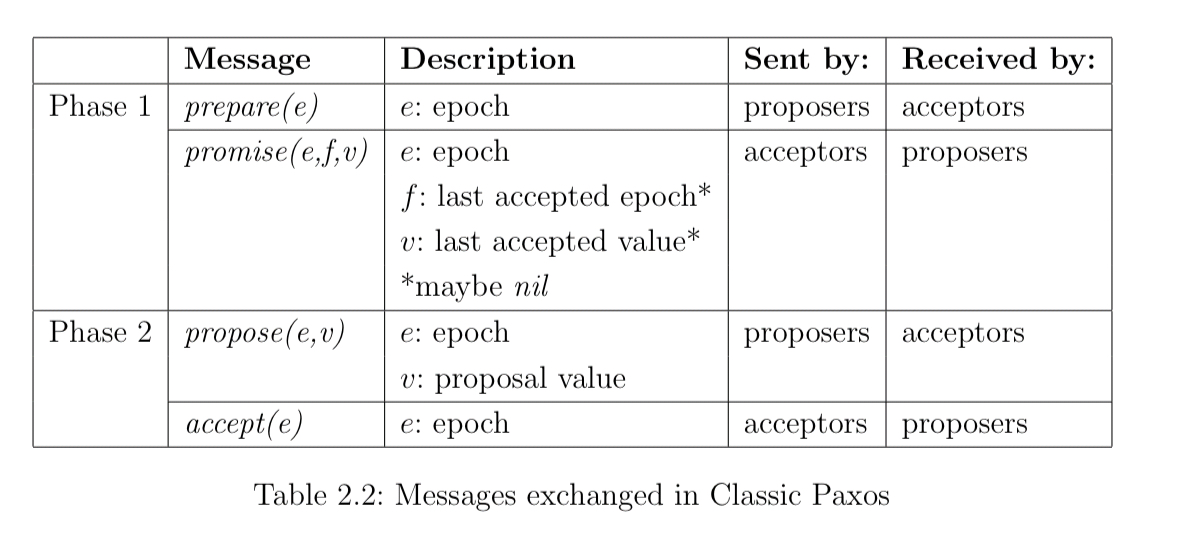
Phase one
- A proposer chooses a unique epoch
and sends
to the acceptors
- Each acceptors stores the last promised epoch and the last accepted proposal. When an acceptor receives
, if
is the first epoch promised or if
is equal to or greater than the last epoch promised, then
is written to storage and the acceptor replies with
where
is the epoch of the last accepted proposal (if any), and
is the corresponding proposed value.
- Once the proposer receives
from the majority of acceptors, it proceeds to phase two.
- If the proposer times out before receiving promises from a majority of acceptors it retries phase one with a greater epoch.
Phase two
- The proposer selects a value
to propose. If no proposals were returned with promises in phase one, then the proposer can choose its own candidate value. If exactly one proposal was returned in phase one, then its value must be chosen. If multiple proposals were returned in phase one, then the proposer must propose the value associated with the greatest epoch. The proposer then sends
to the acceptors.
- When an acceptor receives a
message, if
is the first promised epoch, or is greater than the last promised epoch, then the promised epoch and accepted proposal is update, and the acceptor replies with
.
- Once the proposer receives
from a majority of acceptors, it learns that the value
has been decided.
- If the proposer times out, it retries phase 1 with a greater epoch.
Properties
There are 5 key proposer properties:
- Property 1. Proposers use unique epochs for each proposal
- Property 2. Proposers only propose a value after receiving promises from a majority of acceptors
- Property 3. Proposers only return a value after receiving accepts from a majority of acceptors
- Property 4. Proposers must choose a value according to the value selection rule outlined above in step 1 of phase two.
- Property 5. Each epoch used by a proposer is greater than all previous epochs used by the proposer.
Likewise there are 5 key acceptor properties:
- Property 6. Prepare and propose messages are only processed by an acceptor if the epoch received is greater than or equal to the last promised epoch
- Property 7. If an acceptor does process a message, then its last promised epoch is set to the epoch received.
- Property 8. If an acceptor does process a prepare message, then it replies with promise after satisfying property 7
- Property 9. If an acceptor does process a propose message, it replies with accept after satisfying property 7 and updating its last accepted proposal
- Property 10. The last promised epoch and last accepted proposal are persistent and only updated by properties 7 and 9.
Theorems and Lemmas
The reason for labouring the point so on those properties, is that the safety and progress guarantees of Paxos and then proved in terms of them. Safety is the big one, and the following table summarises the lemmas / theorems (column one), together with the properties that they depend on, as well as the other results they use.
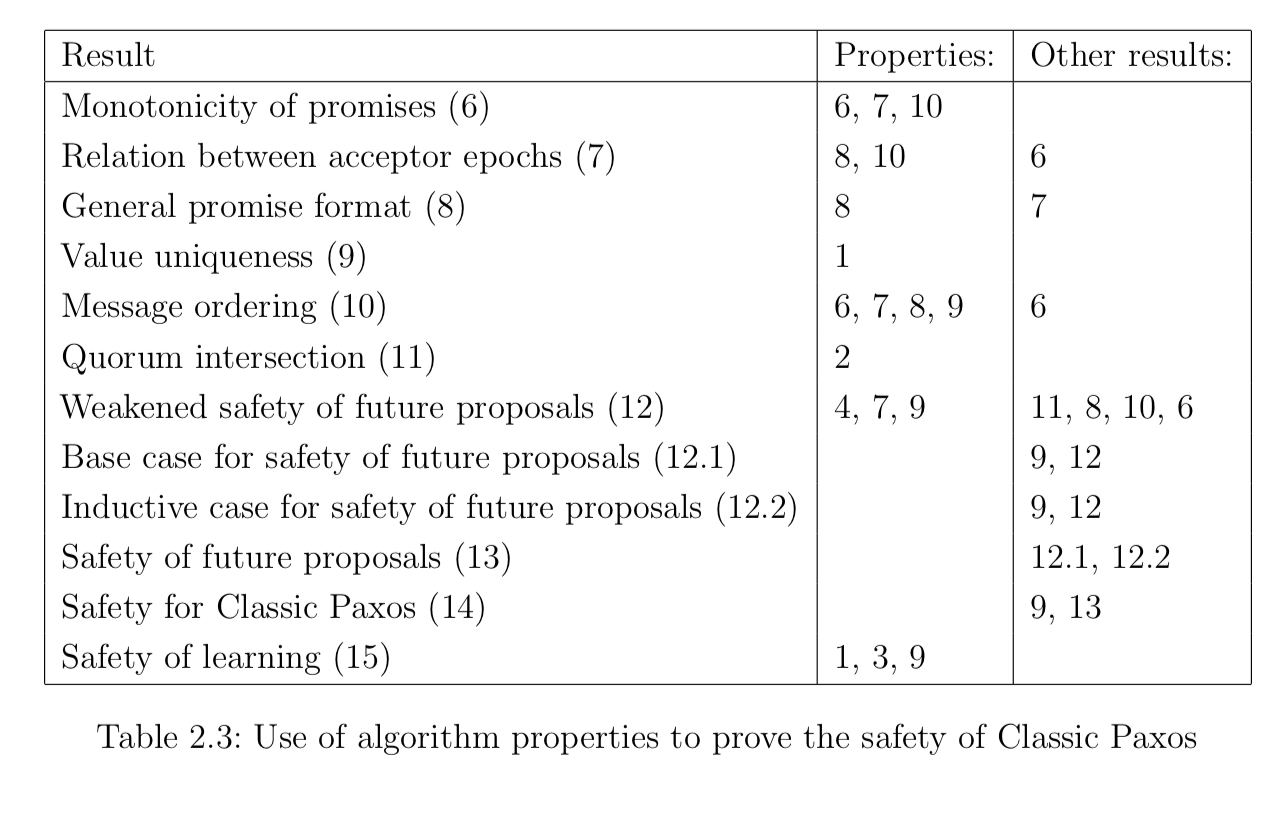
So for example, safety of learning (“If the value is returned by a proposer then
has been decided”), depends only on properties 1, 3, and 9. That is, we could weaken or abandon the other properties, and safety of learning at least would still hold.
Our approach of using multiple layers of intermediate results will allow us to revise this proof throughout this thesis, without reproducing the complete proof.
Proof of progress requires some assumption of liveness conditions for a sufficient period:
- At least a majority of acceptors are live and reply to messages from proposers, within some known upper bound
- Exactly one fixed proposer is live and its relative clock is no faster than some delta ahead of global time (this is to prevent proposers duelling indefinitely)
- Message between the proposer and the majority of acceptors are delivered within a known bound
In the next instalment we’ll look at some of the many variants of classic Paxos.