Keeping CALM: when distributed consistency is easy Hellerstein & Alvaro, arXiv 2019
The CALM conjecture (and later theorem) was first introduced to the world in a 2010 keynote talk at PODS. Behind its simple formulation there’s a deep lesson to be learned with the power to create ripples through our industry akin to the influence of the CAP theorem. It rewards time spent ruminating on the implications. Therefore I was delighted to see this paper from Hellerstein & Alvaro providing a fresh and very approachable look at CALM that gives us an excuse to do exactly that. All we need now is a catchy name for a movement! A CALM system is a NoCo system, “No Coordination.”
When it comes to high performing scalable distributed systems, coordination is a killer. It’s the dominant term in the Universal Scalability Law. When we can avoid or reduce the need for coordination things tend to get simpler and faster. See for example Coordination avoidance in database systems, and more recently the amazing performance of Anna which gives a two-orders-of-magnitude speed-up through coordination elimination. So we should avoid coordination whenever we can.
So far so good, but when exactly can we avoid coordination? Becoming precise in the answer to that question is what the CALM theorem is all about. You’re probably familiar with Brooks’ distinction between essential complexity and accidental complexity in his ‘No silver bullet’ essay. Here we get to tease apart the distinction between essential coordination, a guarantee that cannot be provided without coordinating, and accidental coordination, coordination that could have been avoided with a more careful design.
In many cases, coordination is not a necessary evil, it is an incidental requirement of a design decision.
One of the causes of accidental coordination is our preoccupation with trying to solve consistency questions at lower levels of the stack using storage semantics. There’s an end-to-end argument to be made that we need to be thinking about the application level semantics instead. The lower layers have a part to play, but we can’t unlock the full potential if we focus only there. As Pat Helland articulated in ‘Building on quicksand’, writes don’t commute, but application level operations can. It’s also only at the application level that we can trade coordination for apologies too.
Anyway, here’s the central question:
What is the family of problems that can be consistently computed in a distributed fashion without coordination, and what problems lie outside that family?
Monotonicity
Monotone speech. Monotony. Dull, boring, never a surprise or variation. Monotonic systems are similar, they only ever move in one direction. With monotonicity, once we learn something to be true, no further information can come down the line later on to refute that fact.
Consider deadlock detection in a distributed graph.
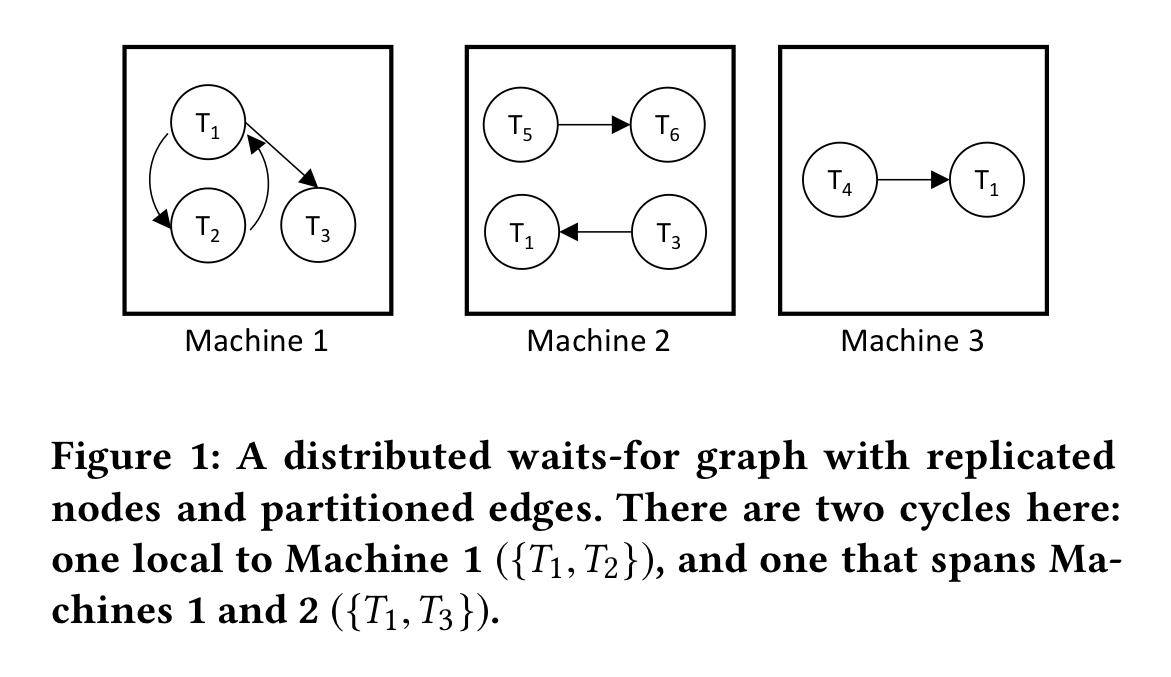
As the machines in the setup above exchange information about the edges they are aware of, then at some point the cycle involving and
will come to light. No matter what other edges are later discovered, we know we have a deadlock. Deadlock detection in this system is monotonic.
Here’s another very similar looking distributed graph, but this time we’re interesting in reachability for the purposes of garbage collection.
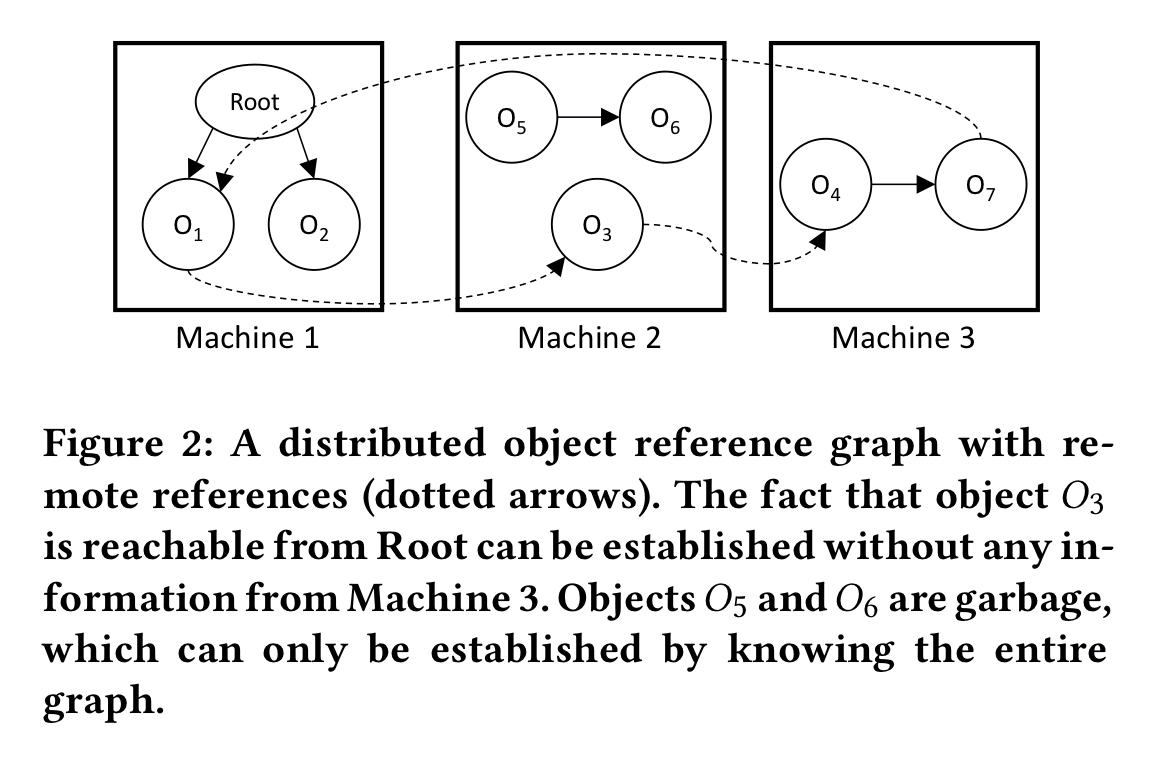
More precisely, we’re interested in unreachability. Based on information to date, we may think that a certain object is unreachable. This property is not monotonic though – the very next edge we uncover could make it reachable again.
In the first instance, we were asking a “Does there exist?” ( ) question. The presence of one positive example gives us an answer in the affirmative and additional positive examples don’t change that fact. In the second instance, we were asking a “Does not exist?” (
) question. We can only answer a question like that once we’ve looked at every example. It’s the same for a “For all…” question (
).
With exactly the same graph, and exactly the same edge discovery algorithm, if we’d been interested in the property of reachability rather than unreachability, then that would have been monotonic. Once we know an object is reachable, finding out it is also reachable via a second path doesn’t change that fact. Unless… our system allows deletion of objects and edges. Then an object that was reachable can become unreachable again, and reachability is no longer monotonic.
What we’ve learned from these examples is that negation and universal quantification mess with monotonicity. We need the property that conclusions made on partial information continue to hold once we have the full information.
This idea of monotonicity turns out to be of central importance. It’s time to meet the CALM Theorem (Consistency as Logical Monotonicity):
Consistency as Logical Monotonicity (CALM). A program has a consistent, coordination-free distributed implementation if and only if it is monotonic.
The CALM theorem delineates the frontier between the possible (that’s the ‘if’ part) and the impossible (the ‘only if’ part). It’s most satisfying that this is also exactly the famous motivational poster message “Keep CALM and Carry On”. If you keep things CALM then you are always in a position to ‘carry on’ without needing to stop and coordinate.

Some more ‘C’ words
We’re making progress. We can now refine our original question to this: “What is the family of problems that can be computed in a monotonic fashion, and what problems lie outside that family?” So far we’ve been talking about CALM, consistency, and coordination. Now we need to introduce a couple more ‘C’ words: commutative and confluent.
Recall that a binary operation is commutative if the order of its operands makes no difference to the result. Addition is commutative, subtraction isn’t. Confluence as applied to program operations is a generalisation of the same idea. An operation is confluent if it produces the same sets of outputs for any non-deterministic ordering and batching of a set of inputs.
Confluent operations compose: if the outputs of one confluent operation are consumed by another, the resulting composite operation is confluent. Hence confluence can be applied to individual operations, components in a dataflow, or even entire distributed programs. If we restrict ourselves to building programs by composing confluent operations, our programs are confluent by construction, despite orderings of messages or execution races within and across components.
Confluent operations are the building blocks of monotonic systems. We still need to take care to avoid negation though (deletions, , and its alternative formulation:
). One creative solution for dealing with negation / deletions, as used for example by CRDT sets, is to keep a separate growing set of deletions alongside additions. In relational algebra terms we can have selection, projection, intersection, join, and transitive closure, but not set-difference. In terms of mutable state we can allow inserts, but not updates and deletes.
The key insight in CALM is to focus on consistency from the viewpoint of program outcomes rather than the traditional histories of storage mutation. The emphasis on the program being computed shifts focus from implementation to specification: it allows us to ask questions about what computations are possible.
CALM in practice
CRDTs provide an object-oriented framework for monotonic programming patterns. We really want to use them within a functional programming context though, or at least one that avoids bare assignment to mutable variables. Immutability is a trivial monotonic pattern, mutability is non-monotonic. Going further, the Bloom language was explicitly designed to support CALM application development:
- Bloom makes set-oriented, monotonic (and hence confluent) programming the easiest constructs for programmers to work with in the language.
- Bloom can leverage static analysis based on CALM to certify when programs provide the state-based convergence properties provided by CRDTs, and when those properties are preserved across compositions of modules.
If you can’t find a monotonic implementation for every feature of an application, one good strategy is keep coordination off the critical path. For example, in the garbage collection example we looked at earlier, garbage collection can run in the background. Another option is to proceed without coordination but put in place a mechanism to detect when this leads to an inconsistency so that the application can “apologise”.
The CALM Theorem presents a positive result that delineates the frontier of the possible. CALM shows that monotonicity, a property of a program, implies consistency, a property of the output of any execution of that program. The inverse is also established: non-monotonic programs require runtime enforcement (coordination) to ensure consistent execution. As a program property, CALM enables reasoning via static program analysis, and limits or eliminates the use of runtime checks.
There’s plenty more good material in the paper itself that I didn’t have space to cover here, so if these ideas have caught your interest I encourage you to check it out.