FairSwap: how to fairly exchange digital goods

~ Adrian Colyer

FairSwap: how to fairly exchange digital goods Dziembowski et al., CCS’18

(Preprint)

This is a transactions paper with a twist. The transactions we’re talking about are purchases of digital assets. More specifically, the purchase of a file (document, movie, archive of a dataset, …). The property we strongly care about is atomicity: either the seller receives payment and the buyer receives a valid file or neither of these things happen. The buyer and seller don’t trust each other (so e.g., “you send me the payment and then I’ll send you the file” is not an acceptable solution, nor is “you send me the file and then I’ll send you the payment”). This is known as the fair exchange problem.

Fair exchange is a well studied research problem. It has been shown that without further assumptions fair exchange cannot be achieved without a Trusted Third Party (TTP). To circumvent this impossibility, research has studied weaker security models— most notably, the optimistic model in which a TTP is consulted only in case one party deviates from the expected behavior.

In many real-world scenarios, escrow services play the role of the trusted third party. Unfortunately this means you do have to trust the escrow service, and often pay a hefty fee.

A promising alternative for implementing escrow services over the Internet is offered by decentralized cryptographic currencies.

The blockchain can hold the escrow state, and smart contracts can implement the exchange rules. It’s time to meet R the receiver (buyer), and S the sender (seller). In the basic scheme R can block some number of coins in the underlying cryptocurrency guaranteeing payment if S sends a valid file to the contract. S can trigger the payout by publishing the file (input x ) to the contract such the the contract can verify its authenticity (e.g. by computing a hashcode and comparing to a value stored in the contract).

That all sounds comparatively straightforward, so what’s the catch? A couple spring immediately to mind. Firstly, publishing the input to the contract as-is enables the contract to verify its validity, but has the side-effect of making the file publicly visible. So unless the seller only wants to sell it once and the buyer is happy for the world to see it post purchase, that’s not great. If we encrypt the file, using e.g. the buyers public key, then how can the contract validate the hash? Secondly, we wanted to avoid paying a hefty few to a traditional escrow service, but storing the whole input file in a contract using probably what is the most expensive storage on the planet!

… in the cryptocurrency Ethereum, which offers rich support for smart contracts, the amount of gas (the currency unit used in Ethereum to pay fees) paid for executing the smart contract strongly depends on two factors: (a) the complexity of the program, and (b) the size of the input x. Concretely, for storing a value x of size 1MB in Ethereum the parties would need to pay more than USD 500 in transaction fees.

Let’s put that in context. As I’m writing this, for your first 50TB, AWS S3 comes in at $0.0023 per GB, so that’s roughly $0.0000023 for one MB, vs $500 in an Ethereum smart contract – 8 orders of magnitude!! A buyer-specific time-limited pre-signed S3 URL accessed over https is a pragmatic approach.

Back in smart contract land, we clearly need to do better than sending the full input to the contract. Using Zero Knowledge Contingent Payments (ZKCP), the seller encrypts x with some key k and computes a cryptographic commitment c = H(k), and a zero knowledge proof that the computation of the ciphertext and the commitment was done with the genuine input x. The seller sends the ciphertext, hash, and zero knowledge proof to the buyer out of band, and the buyer then deploys a smart contract promising to pay p coins to S when the key is published. The contract then just needs to receive the key k and verify the hash.

This works, but the problem is that there’s a large computational burden for the zero-knowledge proofs when the input gets large. The main goal is this paper, FairSwap is to design simple smart contracts that can be executed with low fees, and that put a low computational burden on the participants.

An ideal fair exchange protocol

So far we’ve asserted that we’ll be verifying the validity of an input file x using a hash function, but from now on we’ll make that slightly more generic and discuss some arbitrary input x which can be validated using a predicate function \phi which outputs 1 for a valid input x and 0 otherwise. On that basis, an idealised (three-phase) transaction protocol looks like this:

(‘Sim’ in the above is the ‘simulator’, by convention the name for the real-world adversary being modelled).

In the initialisation phase we receive inputs from both the sender and the receiver and freeze p coins from the receiver if everything looks good. In the reveal phase the receiver learns x. In the final payout phase the sender receives the coins as payment if \phi(x) = 1, otherwise the coins are sent back to the receiver.

This ideal functionality is not yet efficient, but it does have three appealing properties: it will terminate within at most 5 rounds, unlocking all coins from the contract; it is fair to the sender such that an honest sender always receives p coins if the receiver learns the true witness; and it is fair to the receiver such that the receiver only pays p coins if the sender delivers the true witness.

Smart contracts as judges

In the payout phase (round 4) who gets to decide if \phi(x) = 1? The sender doesn’t trust the receiver to make this judgement, and vice versa.

To resolve this conflict, we will use a smart contract to act as a judge… In order to minimize costs for the execution of this contract we do not want the judge contract to learn \phi or x, nor require it to run \phi(x).

The secret to making this efficient is that we assume by default the sender has sent a valid copy of x. If the receiver disagrees, the receiver must create a concise proof of misbehaviour to show that \phi(x) \neq 1. This proof is logarithmic in the circuit size representing \phi.

At a high-level the revised scheme looks like this:

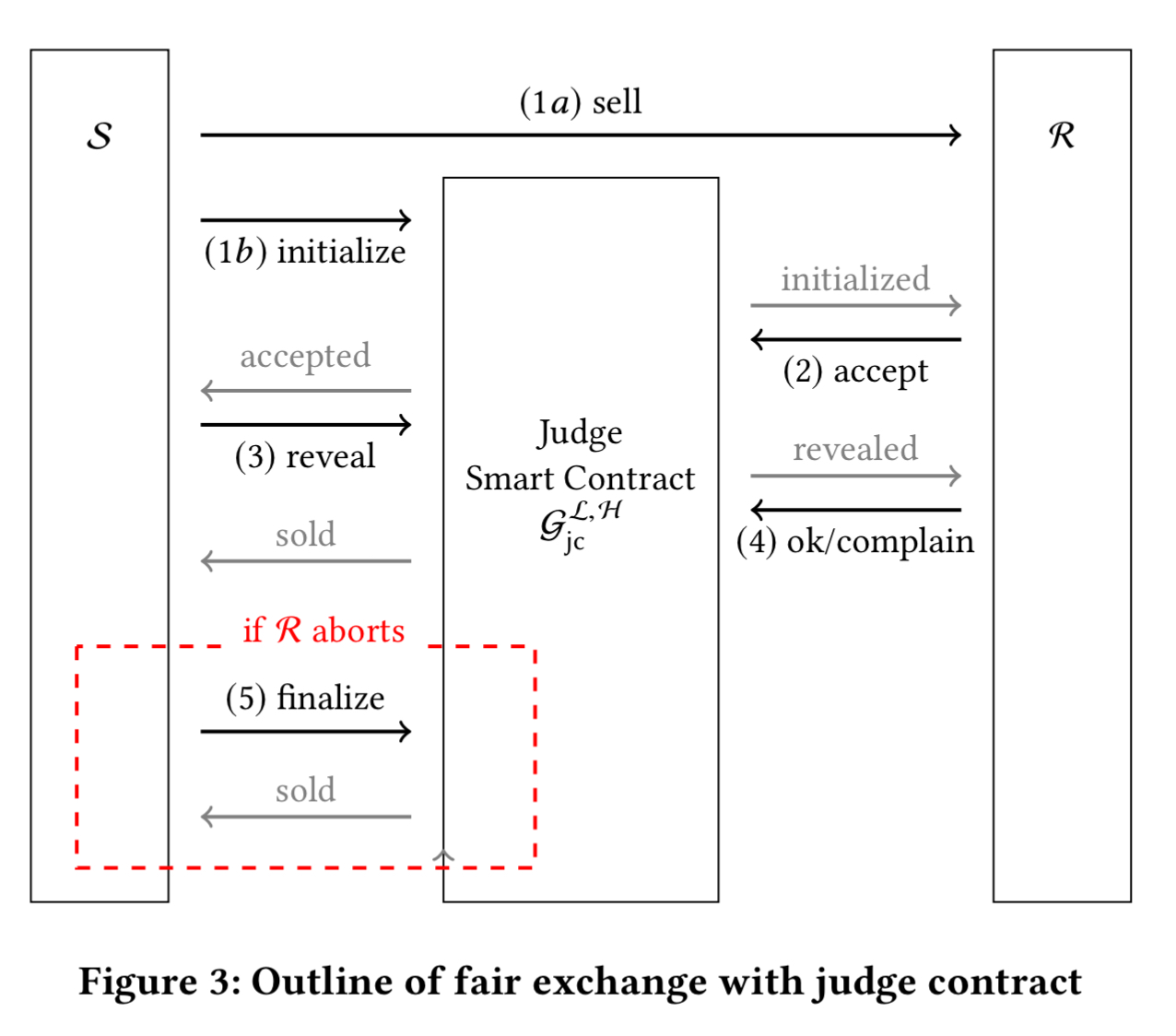
  1. The sender encrypts x and auxiliary information about the computation of \phi(x) and sends the ciphertexts to the receiver (step 1a). The sender also sends a commitment of the key k used for the encryption to the judge contract (step 1b).
  2. The receiver does some preliminary checks, and sends p coins to the contract if they accept.
  3. The sender reveals the secret key k to the judge contract.
  4. The receiver decrypts and verifies the computation of \phi(x). If x is not correct then the receiver produces a concise proof of misbehaviour, and the coins in the contract are refunded.
  5. If the receiver does not complete the protocol in step 4 (by accepting or rejecting) then the sender can finalise the contract and receive the payout.

The Judge smart contract exhibits the following ideal behaviour:

Concise proofs of misbehaviour

Central to all this is the ability to produce a concise proof of misbehaviour.

The key idea is that checking if some part of the claimed computation was carried out incorrectly is much easier than verifying the correctness of the entire computation. In our construction, we let the judge validate only the operation and the result of a single incorrectly computed gate of \phi.

An example makes this all much clearer. Lets go back to the use case of buying a file. We can split the file into n parts and construct a Merkle hash tree from those parts. The circuit representing \phi (computation and verification of the Merkle Hash root) looks like this when n = 8 and each file partitition has size \lambda:

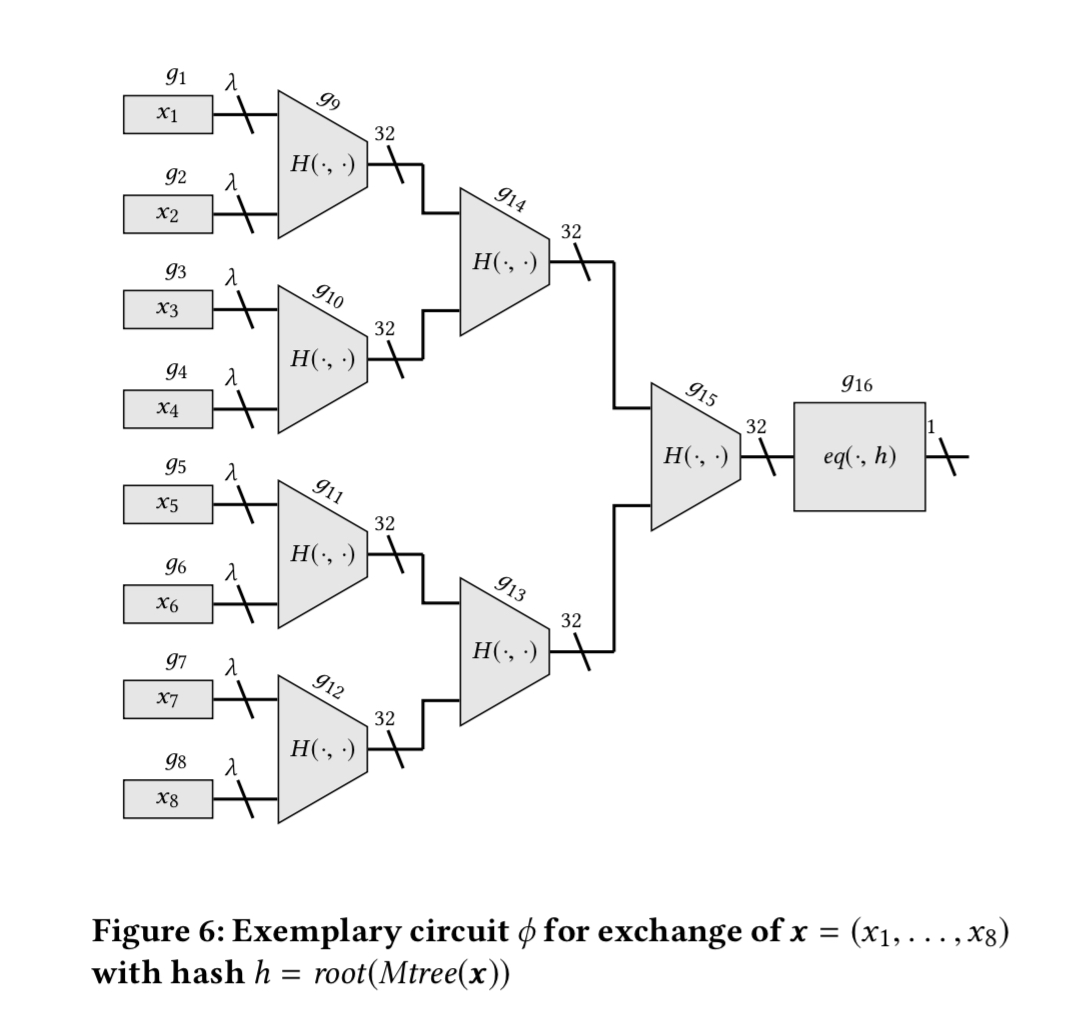
The instruction alphabet of such a circuit consists of just two operations: H(x,y) and eq(x, h) where H is the hash function used in the Merkle tree.

The sender encrypts x and all the intermediate values that are produced during the evaluation of \phi(x). The receiver can then replay the circuit and check that the intermediate values match at every step. If there is a mismatch, the receiver will generate a complaint. The Merkle roots of the circuit and of the tree sent by the sender are both stored in the judge contract so that a receiver can only complain about values genuinely received by the sender, on the basis of the circuit to which both sender and receiver have agreed.

The concise proof of misbehaviour for gate i in the circuit consists of l + 2 Merkle proofs, where l is the number of inputs to the ith gate. Having verified that the l inputs really are the correct inputs, and the claimed gate i really is the i-th gate, the judge computes the output at the gate and checks it matches the output claimed by the sender. If it does not match, the proof of misbehaviour is upheld.

For the file comparison circuit, l = 2 and the instruction alphabet only has two instructions, so we can provide a highly efficient smart contract for this particular use case.

Evaluation

At an exchange rate of $500 USD/Ether as used in the paper, it costs around $1.73 USD to facilitate a fair swap using the contract. As I write this, the actual USD/Ether rate is $122 so it would be even cheaper.

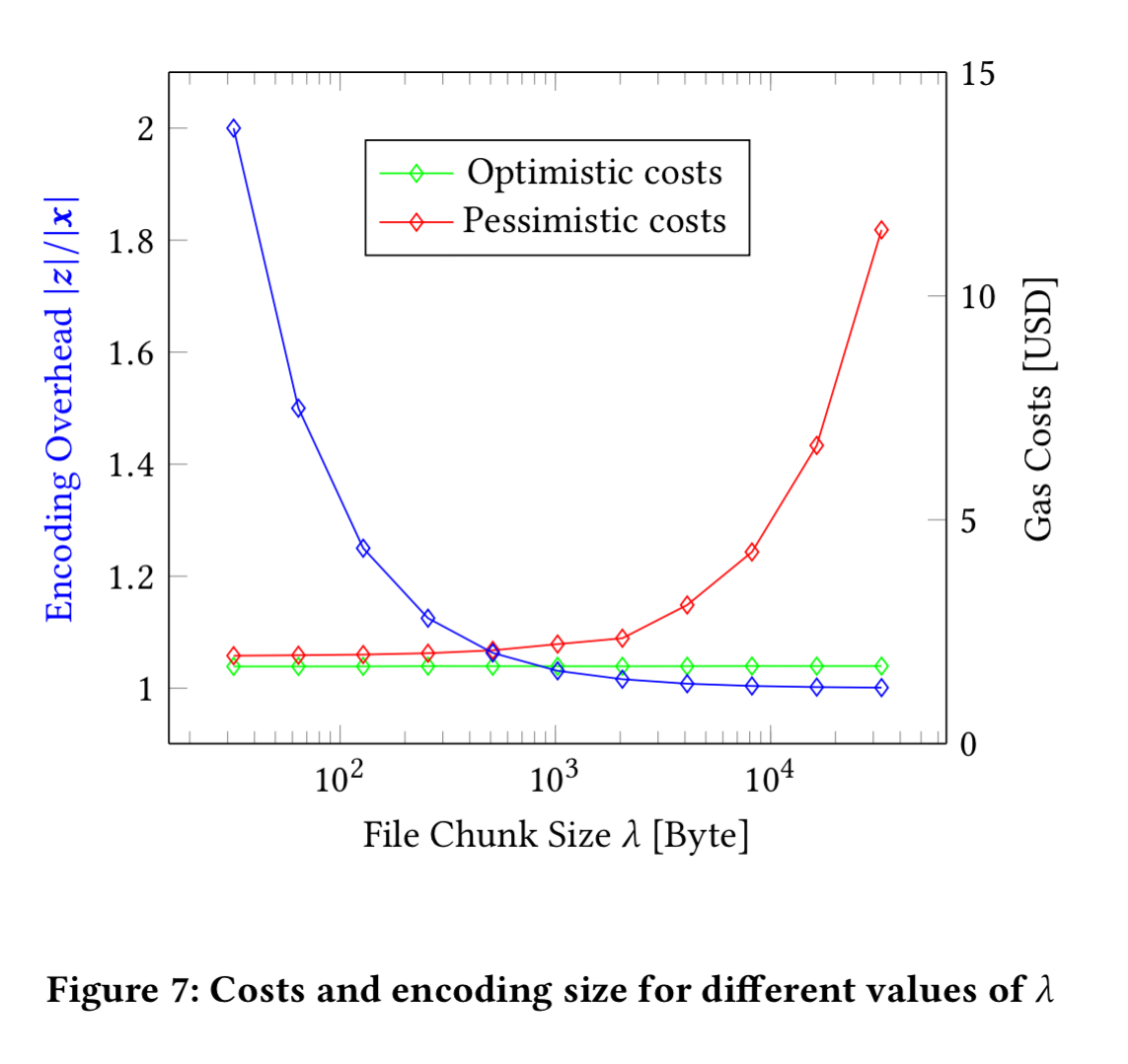
For repeated exchanges between two parties costs can be reduced further by modifying the contract such that it can be used for repeated execution of file sales and run off-chain in a state channel (see section 5.3 in the paper for a brief description).