Online parameter selection for web-based ranking problems

~ Adrian Colyer

Online parameter selection for web-based ranking problems Agarwal et al., KDD’18

Last week we looked at production systems from Facebook, Airbnb, and Snap Inc., today it’s the turned of LinkedIn. This paper describes the system and model that LinkedIn use to determine the items to be shown in a user’s feed:

It replaces previous hand-tuning of the feature mix and ranking:

In the past, a developer spent days to accurately estimate [the feature weights] with desired behavior with every significant drift and intervention. Using the approach described in this paper, we have completely eliminated the laborious manual tuning, significantly increased developer productivity as well as obtained better Pareto optimal solutions.

Here are representative results comparing the impact on three key metrics for a setting found by the new algorithm over a period of 36 hours, vs the best setting that could be found in 7 days of hand-tuning:

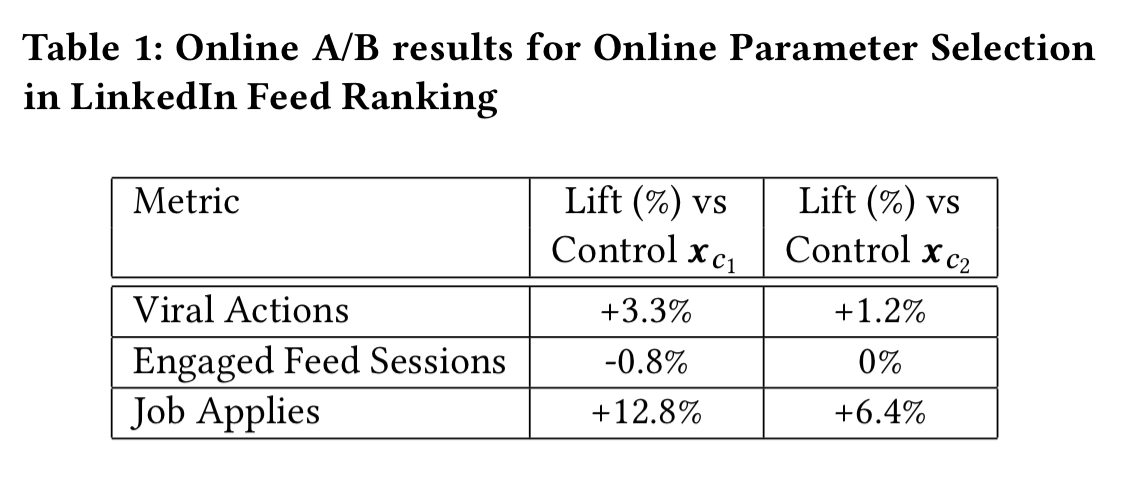
Viral Actions is the most important metric for the LinkedIn feed, ‘with far reaching consequences from more subsequent sessions to more revenue.’ The algorithm is tasked with maximising this metric while not allowing others to drop by more than 1%. (Increases in the other metrics as well are preferred of course).

The overall method is general enough to be applied in settings outside of LinkedIn too.

The LinkedIn feed

The LinkedIn feed includes a variety of content types such as professional updates shared by a member’s connections, native ads posted by advertisers, job recommendations, professional news, and new connection and course recommendations.

The central question here is what items should be shown in the feed of a given user, and in what order.

As each content type usually is associated with a business metric to optimize for, an efficient feed ranking model needs to consider the tradeoff amongst the various metrics…

The three main metrics detailed in the paper are:

  • Viral Actions (VA): the fraction of feed sessions where a user has liked, commented on, or shared a feed item.
  • Engaged Feed Sessions (EFS): the fraction of the total number of sessions where a user was active on the feed.
  • Job Applies (JA): the fraction of sessions where the user applied for a recommended job on the feed.

The ‘feed ecosystem’ (i.e., all the systems providing candidate feed items) is very dynamic. A Feed Mixer first calls each of the downstream feed providing services to retrieve the top-ranked suggestions per feed-type, and then it combines and re-ranks the suggestions across content types to give the final feed.

Each downstream service also provides probability measures for each suggested item, indicating the probability that the member will take the desired action when shown the item. “The estimates of these probability measures are from independent response prediction models and available to the Feed-Mixer in real-time at the time of scoring.”

Multi-objective optimisation

We have multiple different objectives to optimise for (VA, EFS, JA, and so on), which puts us in the world of Multi-Objective Optimization (MOO).

A reasonable approach for balancing multiple objectives is to rank items using weighted linear combinations of the predicted objective utilities.

That’s about as simple as it gets. So we can compute the score of an eligible item with a linear combination like this:

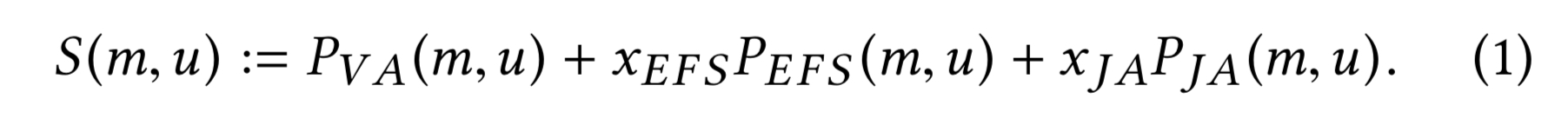
Where P_{metric} is the probability of the member m taking the desired action when shown the item u. A weight vector \mathbf{x} = (x_{EFS}, x_{JA}) controls the balance of the business metrics VA, EFS, and JA. So far so good, there’s just one small issue remaining:

Finding the weights (often called tuning or control parameters) is challenging. Practitioners often rely on running multiple A/B experiments with various values of the control parameters and select the one that works best based on the observed values of the metrics in the experiments. This is a manual and time-consuming process which often needs to be repeated when there is a change in the environment.

We’d like an automated way of finding a good set of control parameters instead.

Thompson sampling

One metric is selected as the primary (VA) in this case, and the other metrics are secondary. The objective therefore is to maximise utility based on the primary metric under the constraint that the utility in the secondary metrics stays above a pre-specified threshold (no more than a 1% drop in the LI case).

With a little massaging the linear combination equation is redefined using Lagrangian weights:


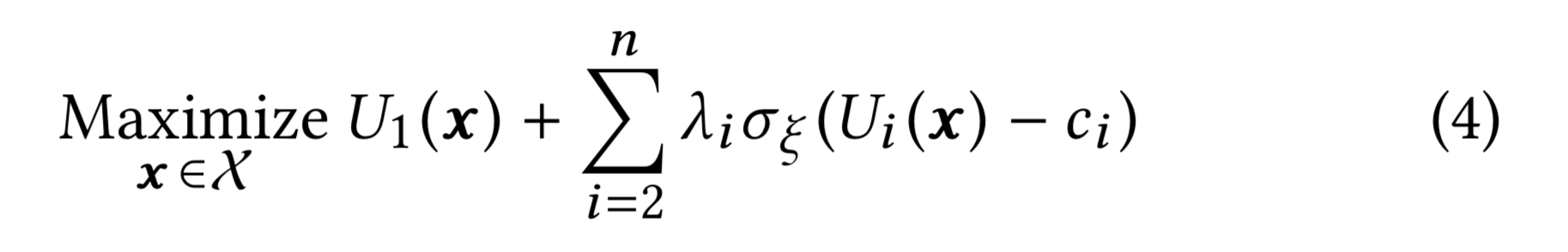
\sigma_{\epsilon}(z) is a smoothing function which evaluates close to 1 for positive z, and close to 0 for negative z. \lambda_i are weights for each of the i candidate items. So what’s going on here is a function that scores a candidate item by summing the \lambda_is for the constraints it satisfies, and adding the utility score in the primary metric.

The trick is to let the value of \lambda_i help us identify how many constraints are satisfied or violated.

This is achieved by setting \lambda_i such that the range the resulting score ends up telling us how many constraints were violated (see section 3 in the paper for details). Doing this we end up with a familiar global optimisation of an unknown function problem.

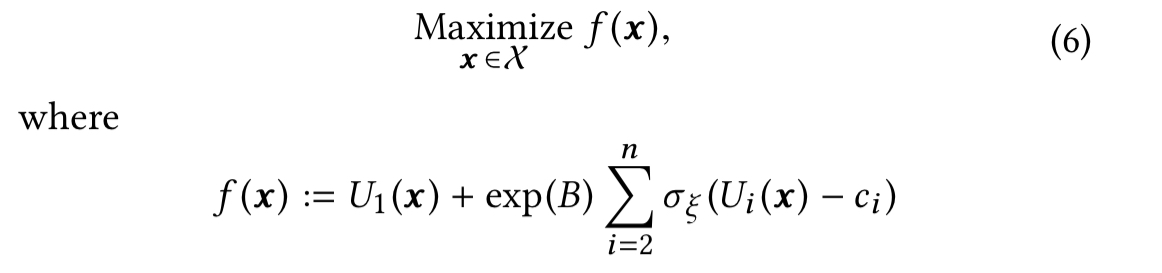
Whether a member takes the desired (per metric) action in a session when their feed is served with parameter \mathbf{x} is modelled as a random variable. After observing the aggregated data for a session this enables us to estimate the respective utilities.

The optimisation problem is solved through a modified version of Thompson sampling. The Thompson Sampling approach samples a new data point \mathbf{x}_t at iteration t from the posterior of the maximiser of f (F_t) given the data we have at stage t-1. The process stops once the variance of the distribution of F_t becomes small, and mode(F_t) is returned as the estimate of the global maximiser. To prevent convergence to a local optimum, the LinkedIn system also explores the entire region \mathcal{X} uniformly (as opposed to just sampling from the posterior) at every iteration t with some probability \epsilon > 0.

The basic algorithm is shown below:

The production system also includes an enhancement to this algorithm as follows: the system searches over a set of grid of values in the entire input space (Sobol points); once it has converged to a small enough region the search space is reduced and more points are generated within it (zooming). The algorithm is stopped when the objective value does not change further through the zooming mechanism.

Figure 4, below, shows a nice example of the algorithm in action.


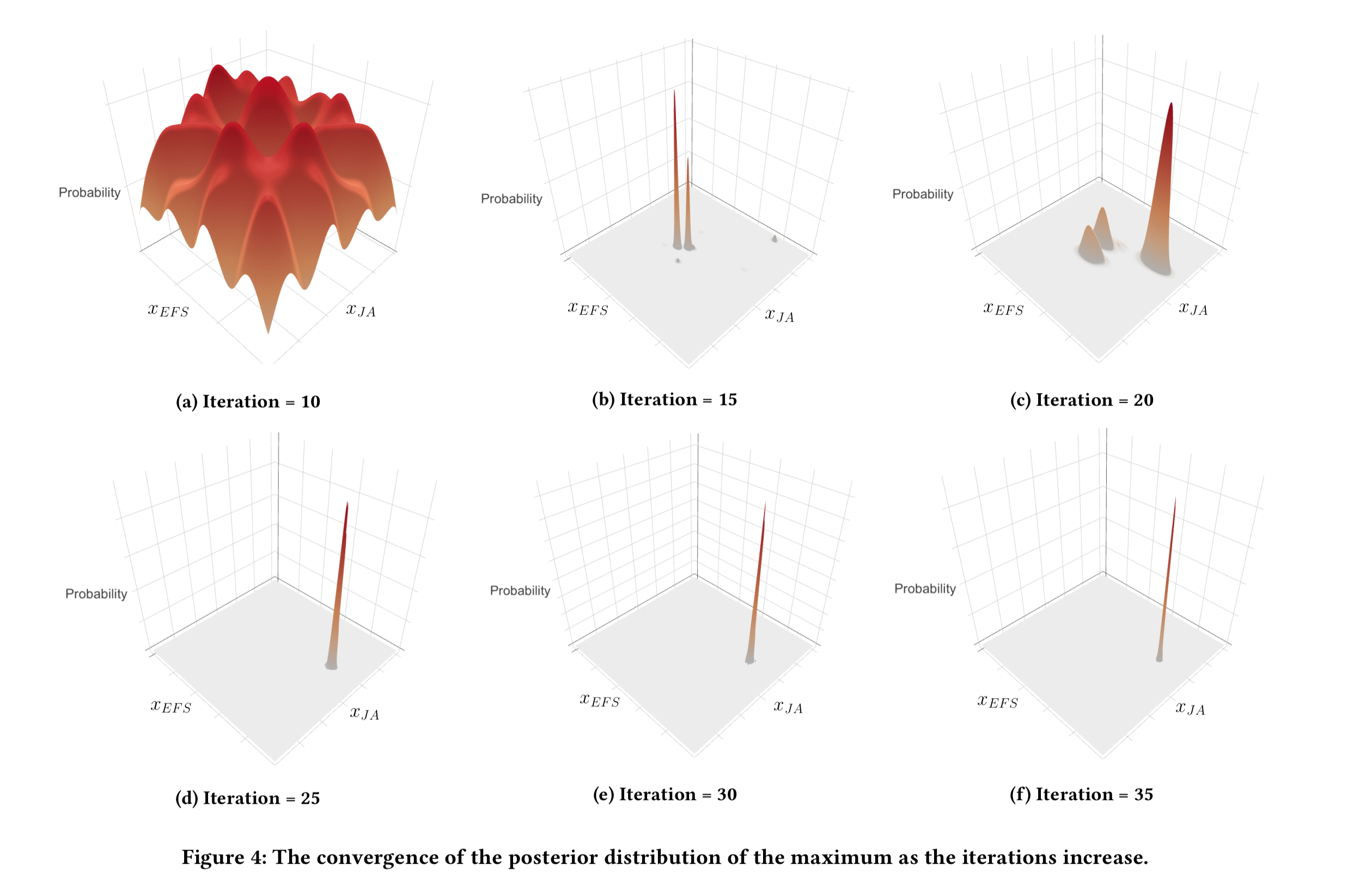
(Enlarge)

  • (a) the algorithm is initialised by performing quasi-random sampling for the first 10 iterations
  • (b) within just 5 more iterations, the algorithm is starting to converge
  • (c) but wait! Stopping early at point (b) would be a mistake as with just one more random sampling step the distribution starts to shift and soon we escape the local optimum and a new peak emerges.
  • (d) now the initial two peaks have disappeared and we have just a single peak
  • (e) by iteration 30 the distribution has become very stable

This experiment shows the importance of choosing the \epsilon -greedy approach; without this adjustment to Thompson Sampling, there is a high probability of getting stuck at a local maximum instead of converging to the true global maximum.

Production system

We have successfully implemented the algorithm in practice and it is deployed in the engineering stack for LinkedIn Feed. We achieved substantial metric gains from this technique and drastically improved developer productivity.

The overall architecture includes online and offline components as shown below.

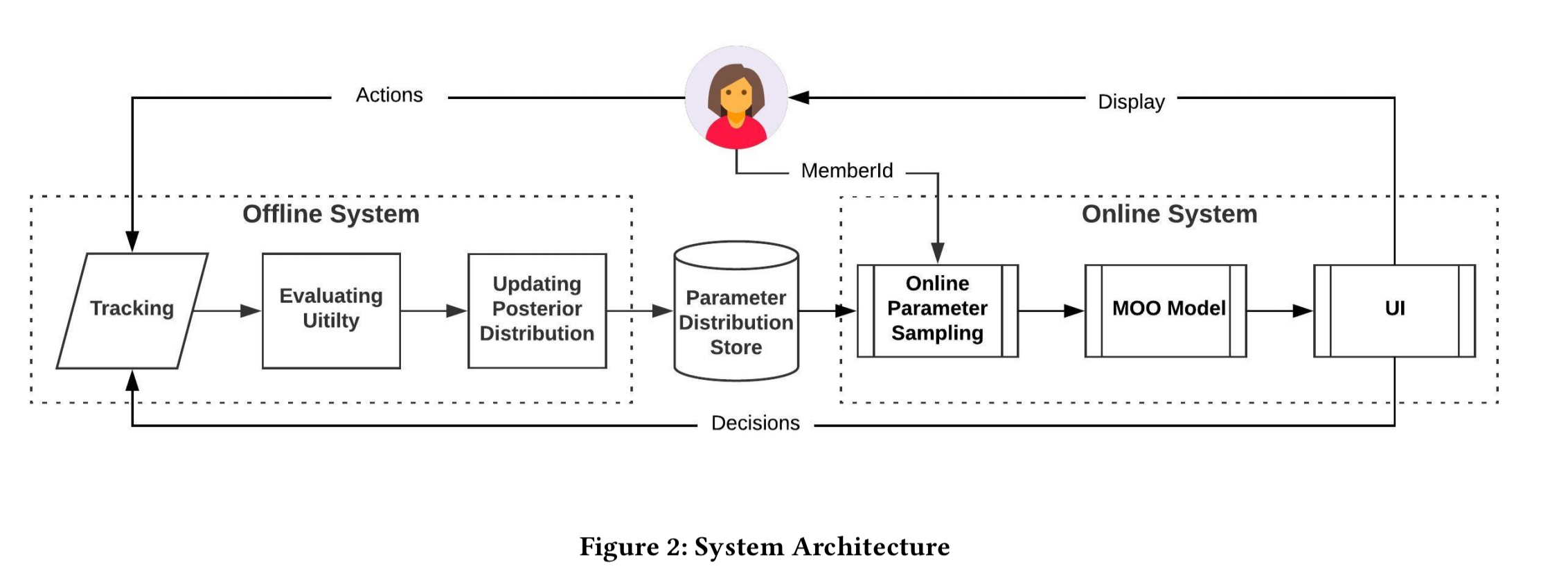
The offline component runs once per hour, calculating the metrics (utilities) based on accumulated tracking data. The metric observations are then used to update the posterior distribution of the maximiser. The resulting distribution is stored in a Voldemort-based KVS.

When a member visits the LinkedIn feed, the online parameter sampling module returns a sample (i.e., a set of weights to configure the feed) from the stored distribution. The sample is based on an MD5 of the user’s memberId, ensuring consistent samples for the same parameter distribution for the same user (so that the feed doesn’t jump around with page refreshes etc.). The sampled parameter value is fed into the MOO models to rank the items received from the feed services, and the resulting ranked list is sent to the UI.