Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding Hundman et al., KDD’18
How do you effectively monitor a spacecraft? That was the question facing NASA’s Jet Propulsion Laboratory as they looked forward towards exponentially increasing telemetry data rates for Earth Science satellites (e.g., around 85 terabytes/day for a Synthetic Aperture Radar satellite).
Spacecraft are exceptionally complex and expensive machines with thousands of telemetry channels detailing aspects such as temperature, radiation, power, instrumentation, and computational activities. Monitoring these channels is an important and necessary component of spacecraft operations given their complexity and cost. In an environment where a failure to detect and respond to potential hazards could result in the full or partial loss of spacecraft, anomaly detection is a critical tool to alert operations engineers of unexpected behavior.
Anomaly detection systems deployed today typically consist of tiered alarms indicating when values fall outside of pre-defined limits. There are also limited instances of expert systems and nearest-neighbour based approaches being tried, but their limitations prevented widespread adoption. A more accurate and scalable approach to anomaly detection that makes better use of limited engineering resources is required.
Any such system needs to work with data that is highly context dependent and often heterogeneous, noisy, and high-dimensional. Any anomalies reported should come with a degree of interpretability to aid diagnosis, and a balance must be struck between false positives and false negatives. This paper focuses on reported anomalies and telemetry data for the Soil Moisture Active Passive (SMAP) satellite and the Mars Science Laboratory (MSL) rover, Curiosity.
An open source implementation of the the methods described in this paper, together with incident data and telemetry, is available at https://github.com/khundman/telemanom.
LSTMs to the rescue?
In the terminology of this paper there are three categories of anomaly of interest:
- Point anomalies are single values that fall within low-density regions of values
- Collective anomalies are sequences of values that are anomalous, whereas any single value in the sequence by itself might not be, and
- Contextual anomalies are single values that do not fall within low-density regions of values overall (i.e., they’re not ‘out of limits’), but they are still anomalous with regards to the sequence of local values they are embedded in.
Compared to previous generations of automated anomaly detection, recent advances in deep learning, compute capacity, and neural network architectures hold promise of a performance breakthrough:
LSTMs and related RNNs represent a significant leap forward in efficiently processing and prioritizing historical information valuable for future prediction…. The inherent properties of LSTMs makes them an ideal candidate for anomaly detection tasks involving time-series, non-linear numeric streams of data. LSTMs are capable of learning the relationship between past data values and current data values and representing that relationship in the form of learned weights.
Other advantages of LSTMs for anomaly detection include:
- they can handle multivariate time-series data without the need for dimensionality reduction
- they don’t require domain knowledge of the specific application, allowing for generalisation
- they can model complex non-linear feature interactions
- there is no need to specify time windows for shared data values
NASA’s LSTM-based system has three parts:
- LSTM-based value prediction, learned in an unsupervised fashion from normal command and telemetry sequences.
- An unsupervised thresholding method that looks at the differences between the value predictions and the actual values to determine whether prediction errors are indicative of true anomalies
- A set of filters to further mitigate false positives
Value prediction
The LSTM models used for value prediction use input sequences of length 250 and are configured as follows:
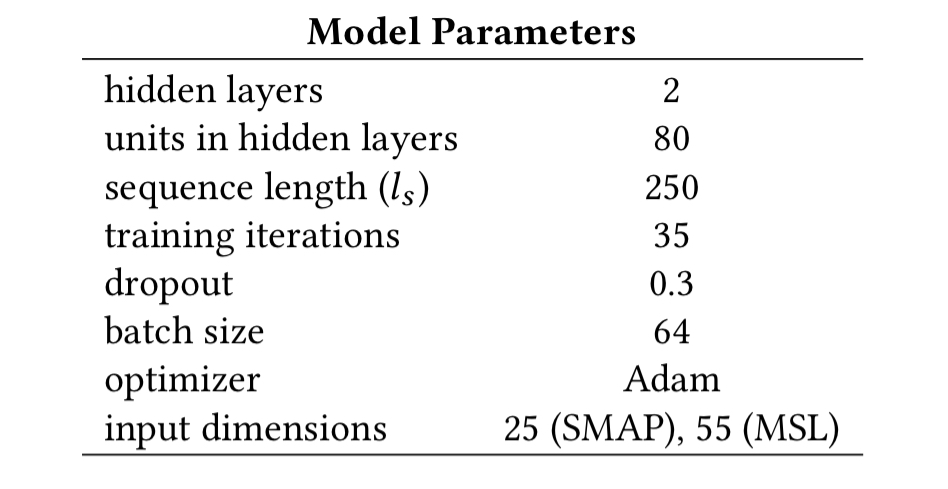
A single model is created for each telemetry channel and used to predict values for that channel only. This helps with traceability when investigating reported anomalies (versus predicting m values from a single model) and avoids LSTM problems with accurately predicting m-dimensional outputs for large m.
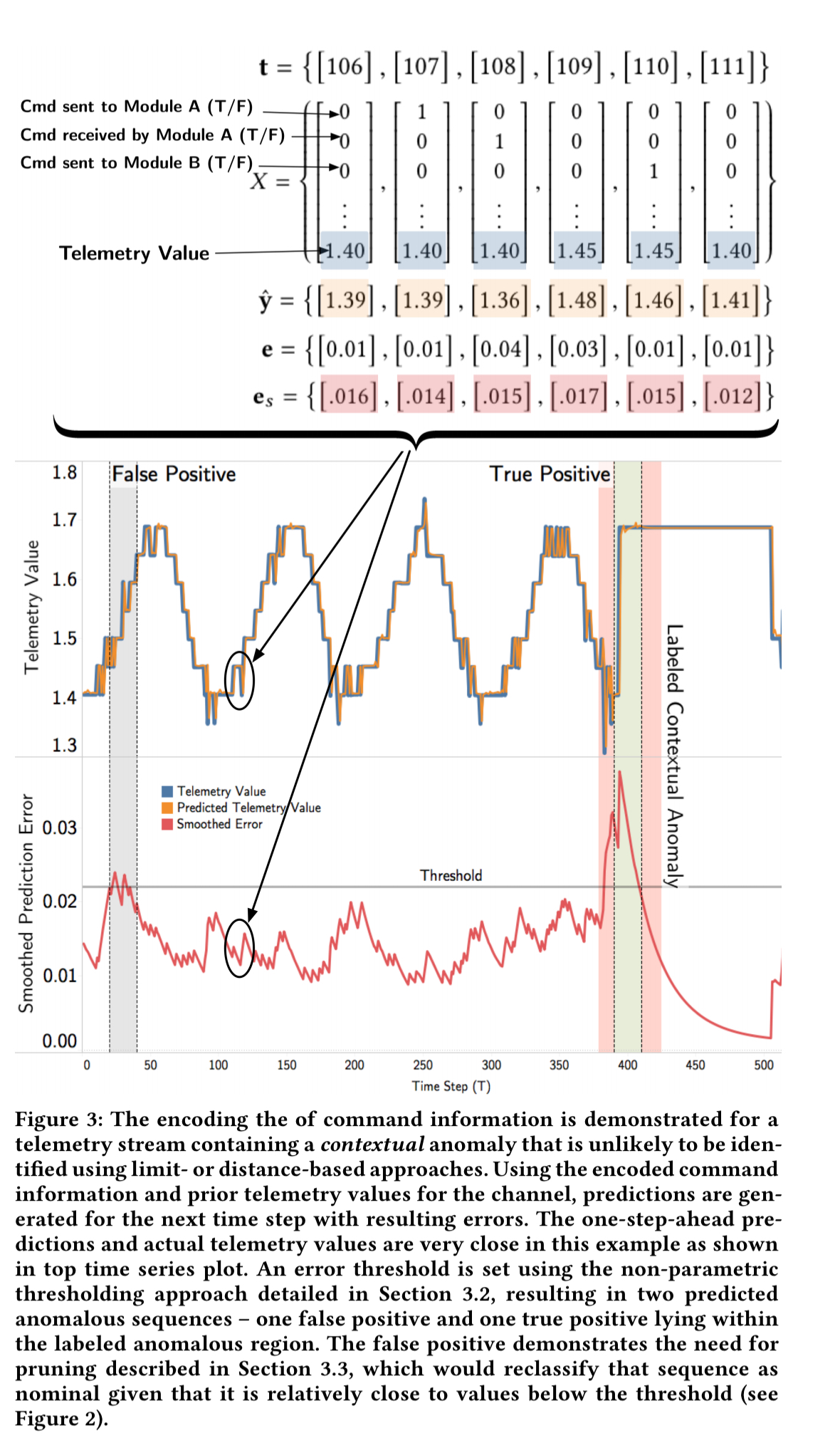
The time series inputs comprise the telemetry values together with a one-hot encoding of the commands sent to the spacecraft.

Each model is tasked with predicting only the next value (i.e., an output sequence of length 1).
Dynamic error thresholds
Taking the delta between the predicted value and the actual next value in the telemetry stream gives us a stream of prediction errors. A window of h historical error values is then used to smooth these errors using an exponentially-weighted moving average:
The set of errors are smoothed to dampen spikes in errors that frequently occur with LSTM-based predictions — abrupt changes in values are often not perfectly predicted and result in sharp spikes in error values even when this behavior is normal.
Given the smoothed values, we can now apply a simple threshold test to detect candidate anomalies. But how should we set the threshold?
Let the sequence of smoothed error values be . The threshold
is selected from the set
using the argmax function, where z is drawn from an ordered set of positive values representing the number of standard deviations above . The evaluation used { 2.5, 3.0, 3.5, … 10.0 }.
Once has been determined from this set, it is used to compute an anomaly score indicating the severity of the anomaly.
In simple terms, a threshold is found that, if all values above are removed, would cause the greatest percent decrease in the mean and standard deviation of the smoothed errors. The function also penalises for having larger numbers of anomalous values and sequences to prevent overly greedy behavior. Then the highest smoothed error in each sequence of anomalous errors is given a normalized score based on its distance from the chosen threshold.
Mitigating false positives
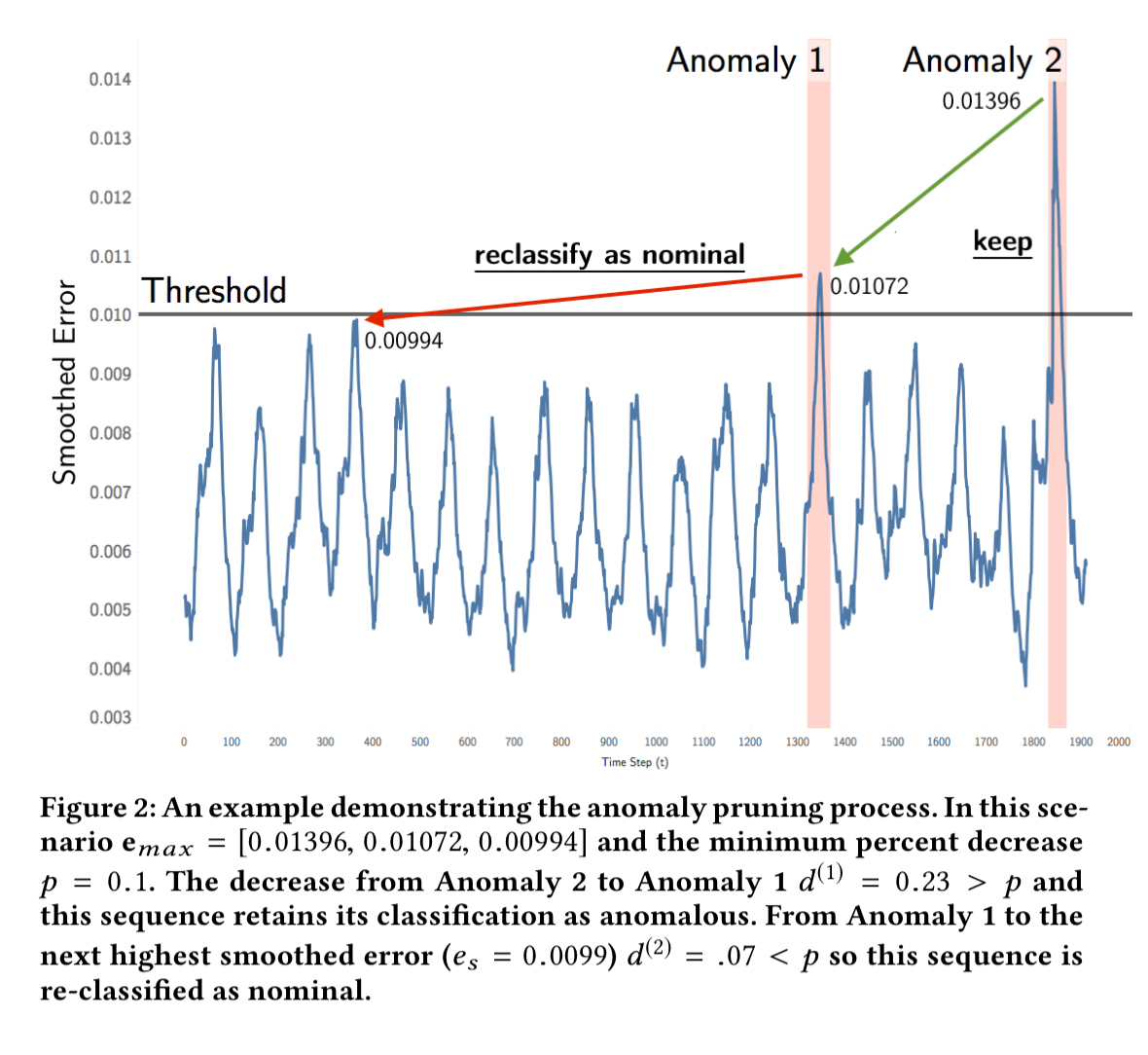
Since false positives are expensive a further pruning stage is now applied. We map max over each anomaly-containing smoothed window of prediction errors, and finally add the maximum smoothed error that isn’t anomalous to the resulting set, . Now
is sorted in descending order. From the sorted sequence, the percentage decrease
at each step
is calculated. E.g., if we have a max sequence (10, 8, 6, 3, 1) then the first percentage decrease will be (10-8)/10 = 20%.
A threshold p is now chosen to represent the minimum percent different between subsequent anomalies (p = 0.13 in the evaluation). When a decrease exceeds the threshold p, all preceding sequences remain flagged as anomalous. If a decrease does not exceed p, and nor do any subsequent decreases, then the following smoothed error sequences are reclassified as nominal.
With sufficient historical data, it is also possible to set a minimum anomaly score threshold such that any anomaly scoring below this is reclassified as nominal.
Evaluation
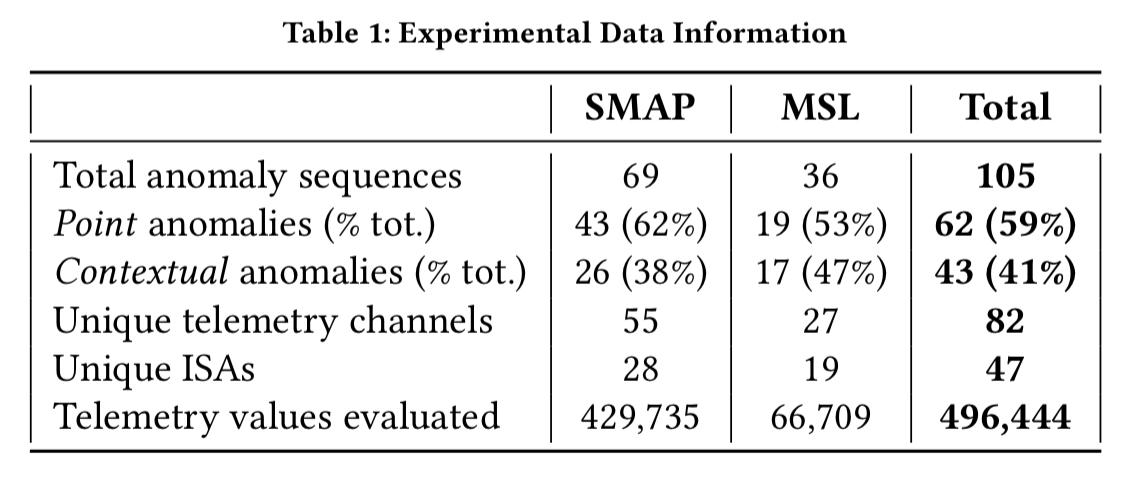
The evaluation is done base on telemetry data from SMAP and MARS, coupled with information on anomalies from Incident, Surprise, Anomaly (ISA) reports. For each unique stream of data containing one or more anomalous sequences a 5 day window of data is constructed around the primary anomaly. This window of data becomes part of the test data set. A further 2 day window immediately prior to the start of the test window is used for training.
Telemetry values are aggregated into one minute windows and evaluated in batches of 70 minutes, which matches the downlink schedule for SMAP. The size of the smoothing window, h , is set at 2100. Here are the results for each spacecraft:
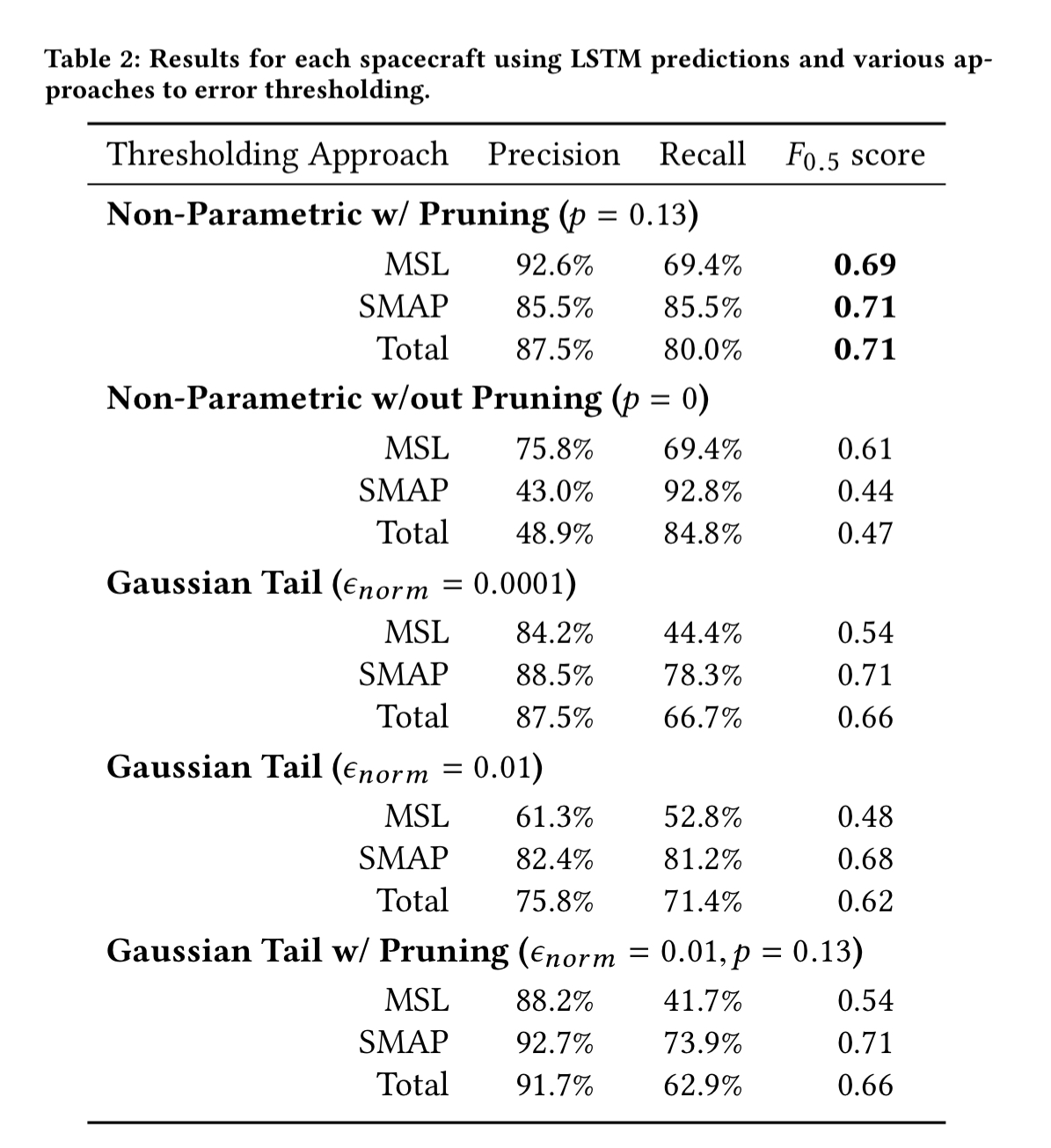
The LSTM models achieved an average normalized absolute error of 5.9% predicting telemetry values one time step ahead…. The high proportion of contextual anomalies (41%) provides further justification for the use of LSTMs and prediction-based methods over methods that ignore temporal information. Only a small subset of the contextual anomalies — those where anomalous telemetry values happen to fall in low-density regions — could theoretically be detected using limit-based or density-based approaches.
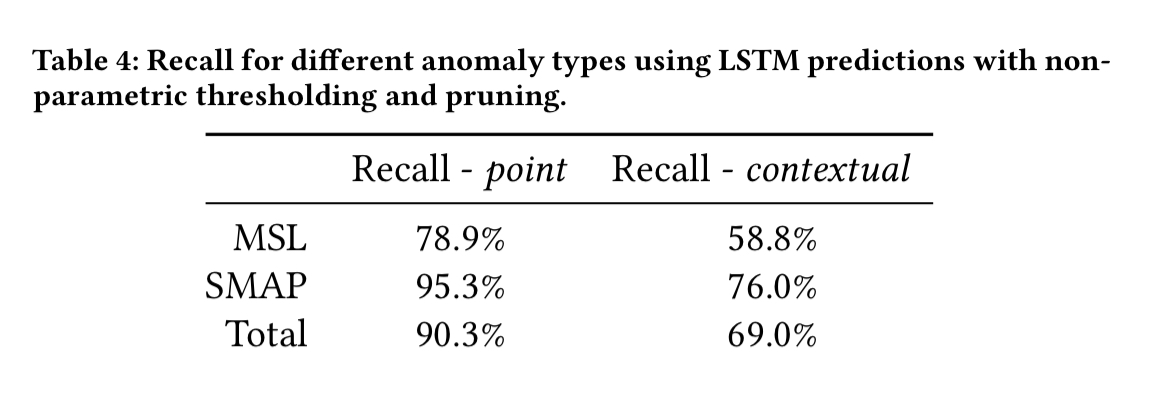
MSL performs a much wider set of behaviours than SMAP, with varying regularity, which explains the lower precision and recall for MSL ISAs.
Deployment
The methods presented in this paper have been implemented into a system that is currently being piloted by SMAP operations engineers. Over 700 channels are being monitored in near real-time as data is downloaded from the spacecraft and models are trained offline every three days with early stopping. We have successfully identified several confirmed anomalies since the initial deployment in October 2017.
The major issue being worked on now is to reduce the number of false positives (the bane of many an alerting system!): “Investigation of even a couple of false positives can deter users and therefore achieving high precision with over a million telemetry values being processed per day is essential for adoption.”
Also in future work is investigating the interactions and dependencies between telemetry channels, giving a view onto the correlation of anomalies across channels (which feels like it also ought to help reduce the false positive rate as well).