Fairness without demographics in repeated loss minimization Hashimoto et al., ICML’18
When we train machine learning models and optimise for average loss it is possible to obtain systems with very high overall accuracy, but which perform poorly on under-represented subsets of the input space. For example, a speech recognition system that performs poorly with minority accents.
We refer to this phenomenon of high overall accuracy but low minority accuracy as a representation disparity… This representation disparity forms our definition of unfairness, and has been observed in face recognition, language identification, dependency parsing, part-of-speech tagging, academic recommender systems, and automatic video captioning.
For systems that are continually trained and evolved based on data collected from their users, the poor performance for a minority group can set in place a vicious cycle in which members of such a group use the system less (because it doesn’t work as well for them), causing them to provide less data and hence to be further under-represented in the training set…
… this problem of disparity amplification is a possibility in any machine learning system that is retrained on user data.
An interesting twist in the problem is that the authors assume neither the number of groups (K), nor group membership, is known. An online speech recognition system for example, is unlikely to collect demographic information on its users. We simply assume that there will be groups, and then bound the worst-case risk for any group.
Our work can be seen as a direct instantiation of John Rawl’s theory on distributive justice and stability, where we view predictive accuracy as a resource to be allocated. Rawls argues that the difference principle, defined as maximizing the welfare of the worst-off group, is fair and stable over time since it ensures that minorities consent to and attempt to maintain the status quo.
After showing that representation disparity and disparity amplification are serious issues with the current status quo, the authors go on to introduce a method based on distributionally robust optimization (DRO) which can can control the worst-case risk.
We demonstrate that DRO provides a upper bound on the risk incurred by minority groups and performs well in practice. Our proposed algorithm is straightforward to implement, and induces distributional robustness, which can be viewed as a benefit in and of itself.
Representation disparity and disparity amplification
We have a population with latent groups. Each group
is a proportion
of the overall population, and has a distribution
. We have some trained model with parameters
used to make predictions based on an input
arising from one of the latent groups. When a user makes a query, they incur some expected loss, which is termed the risk
in this paper.
Representation disparity occurs when there is a meaningful gap between the overall risk and the maximum (worst-case) group risk
. I.e., good overall performance, but poor performance (higher expected loss) for the worst-case group in K. In the evaluation example, the task is text prediction for autocomplete and the training data set contains a mix of African-American English (AAE) and Standard-American English (SAE) tweets. If the AAE data is in the minority, we would expect worse than average model performance when autocompleting African-American English. The measure of the representation disparity is given by
.
Disparity amplification is the process by which unbalanced group risk gets worse over time.
Consider a system which learns from its users, with periodic re-training. Say there are T rounds of such training. Within each round we might gain some new users and lose some existing users (aka churn). The authors make the reasonable assumption that user retention within a group is a strictly decreasing function of risk level (i.e., the worse the system performs for a group, the fewer users of that group are retained). The decrease in user retention for a minority group as compared to the average causes the group size to shrink, meaning that in the next round it will receive even higher losses due to having fewer samples from the group in the training data.
To keep a handle on the representation disparity, we want to control (minimize) the worst-case group risk over all time periods in
.
Roughly speaking, minimizing the worst-case risk should mitigate disparity amplification as long as lower losses sead to higher user retention.
For a system to be fair over the long term there needs to be a stable and fair fixed-point for the expected user counts over time. That is, risk minimisation needs to maintain the same population fraction over time. It’s easy to violate this condition when minimising overall risk (the standard empirical risk minimization, ERM, approach), even when we start out with two groups that have identical population size and initial risk.
In the following example we have two initially equal groups (one on the left, one on the right), and a classifier tasked with classifying points as red or black. Start out with a classifier with boundary (optimal for this data set). Now let optimisation play out over
rounds. At some point in the earlier rounds, due to random fluctuations in sampling accuracy, we took slightly fewer samples from the cluster on the right, meaning that ERM improves the loss for the left cluster at the expense of the right-hand one (see e.g. the
line). This increases churn in the right-hand cluster, reducing its representation in future rounds. Once the scales have tipped even slightly like this the disparity is amplified until at
there are nearly no samples from the right-hand cluster and it ends up suffering high loss.
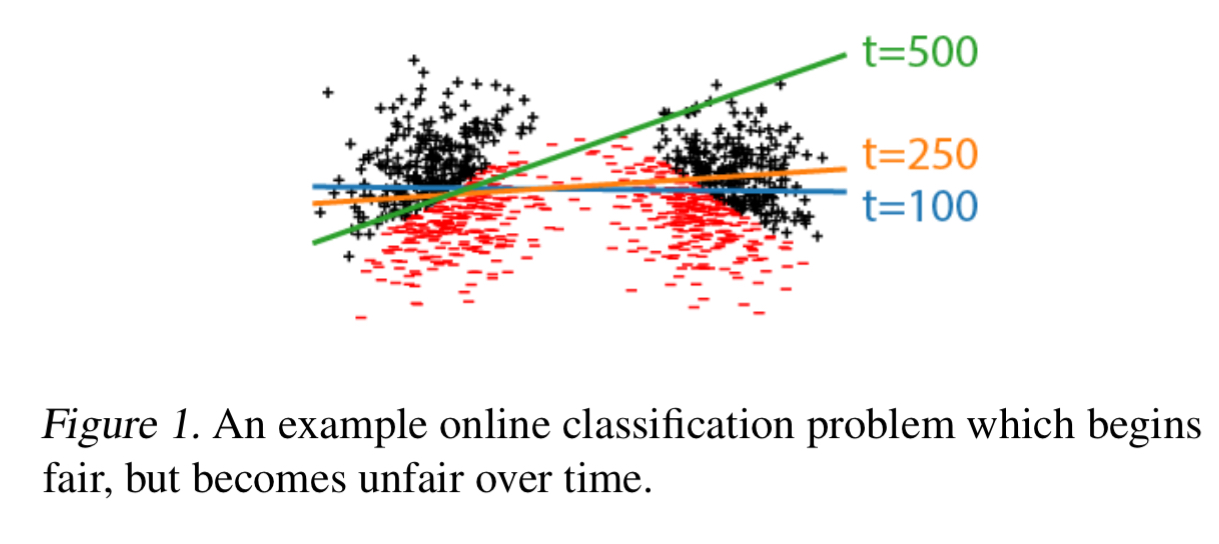
Whenever decreasing the risk for one group increases the risk for others sufficiently the fixed point will be unstable and the model will converge to a different, possibly unfair, fixed point.
Distributionally robust optimization
Clearly we might not want to use ERM if we are concerned about representation disparity and its amplification. But what should we use instead? We need something that minimises the worst-case risk over time. If we can control the worst-case risk in one time step, then by an induction-like argument you can see that we can control it over all time steps.
The fundamental difficulty in controlling the worst-case risk over a single time step comes from not observing the group memberships from which the data was sampled… To achieve reasonable performance across different groups, we postulate a formulation that protects against all directions around the data generating distribution.
Distributionally robust optimization, DRO, has roots going back to 1958 (Ye, ‘Distributionally robust stochastic and online optimization’ ) and deals with optimisation in situations where you are not sure of (or an adversary controls, within some bounds), the true underlying distribution.
In this case, what the authors do is consider all possible distributions within a distance r of the overall population distribution
, where r is the chi-squared divergence measure between the two distributions. The result is a ‘chi-squared ball’. Let
be the worst-case loss over all the r-perturbations around P. The authors show that this bounds the risk of the group
and hence the overall worst-case risk.
If the smallest minority group proportion we want to consider is , then we can control the worst-case group risk by minimizing the upper bound of
with
. See §4.1 in the paper for details. Under the covers what happens is that small levels of loss get ignored, and large losses above a threshold are upweighted due to a square term. My statistics knowledge isn’t good enough to take you any deeper here!
Fortunately, if you just want to put this into practice without diving into all the underlying theory, you just need to need to use the following optimisation objective:
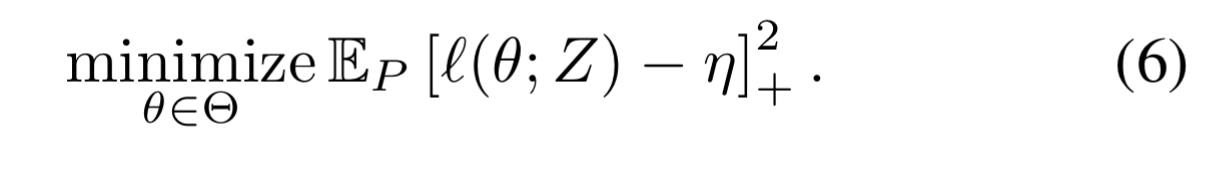
Where is a hyperparameter.
Evaluation
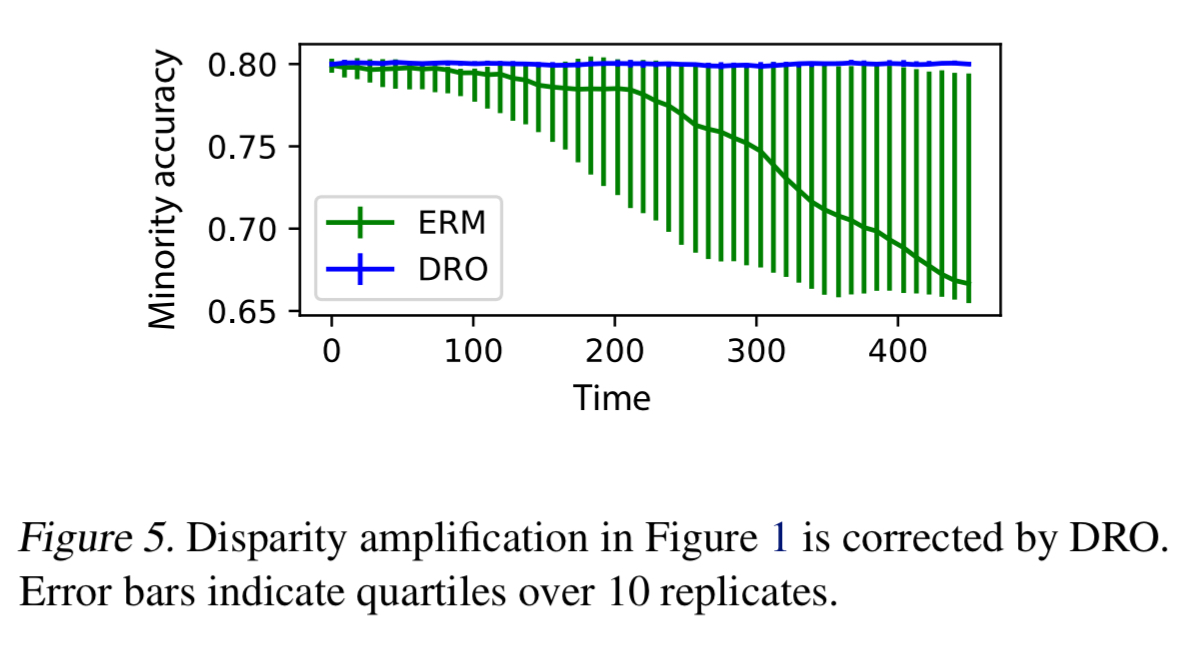
Recall the experiment with two equal left and right groups and a red/black classifier that we looked at earlier. This was unstable under ERM, with a minority group emerging and classification accuracy for that minority group getting worse over time. If we run the same experiment with DRO, the disparity amplification effect disappears.
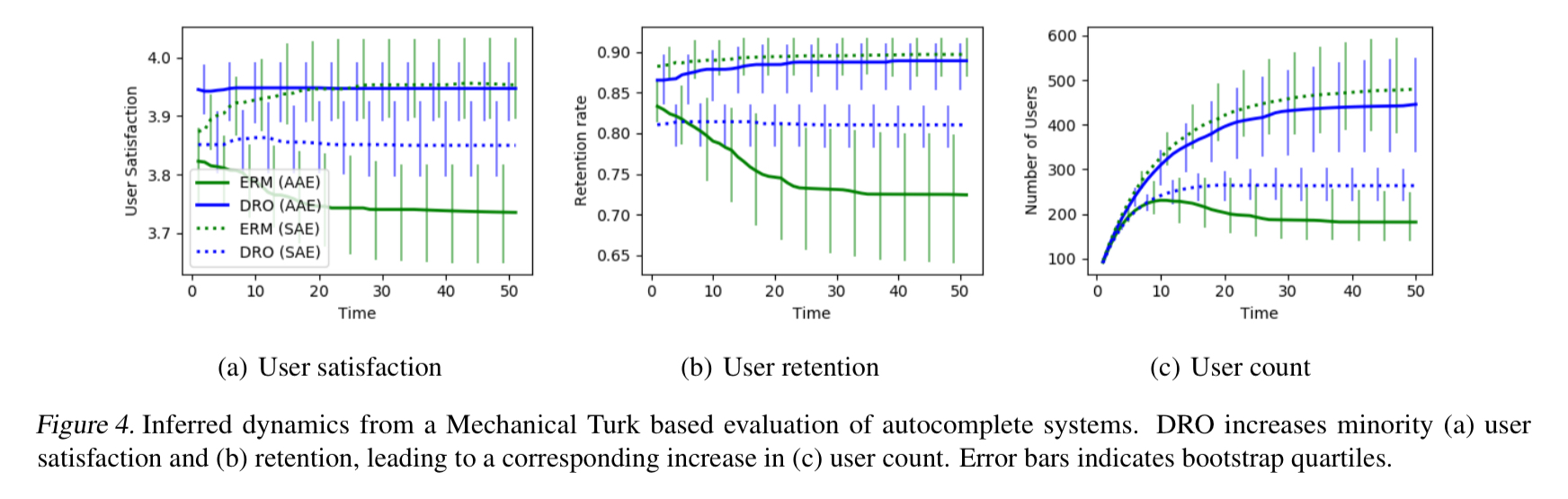
The authors also complete a real-world human evaluation of user retention and satisfaction on a text autocomplete task (with a mix of African-American Engish and Standard-American English training examples as described earlier).
For both ERM and DRO, we train a set of five maximum likelihood bigram language models on a corpus with 366,361 tweets total and a
fraction of the tweets labelled as AAE. This results in 10 possible autocomplete systems a given Mechanical Turk user can be assigned to during a task.
The results show an improvement in both minority satisfaction and retention rate with DRO, with only slightly decreasing scores for the SAE group.
(Enlarge)
The code to generate results is available on CodaLab. (CodaLab itself looks pretty interesting btw. – ‘a collaborative platform for reproducible research’).
5 thoughts on “Fairness without demographics in repeated loss minimization”
Comments are closed.