Bounding data races in space and time Dolan et al., PLDI’18
Yesterday we looked at the case for memory models supporting local data-race-freedom (local DRF). In today’s post we’ll push deeper into the paper and look at a memory model which does just that.
Consider a memory store 
Every thread has a frontier, F, which is a map from non-atomic locations to timestamps.
Intuitively, each thread’s frontier records, for each nonatomic location, the latest write known to the thread. More recent writes may have occurred, but are not guaranteed to be visible.
For atomic locations, the memory store records a pair (F,x), with a single data value x rather than a history. F is a frontier, which will be merged with the frontiers of threads that operate on the location. This is expressed in the rules READ-AT and WRITE-AT in the operational semantics below. The READ-AT rule, for example, should be read as “when a thread with frontier F reads a memory location A with content (Frontier-A, x), then the memory location is unchanged and the new frontier of the thread is F union Frontier-A”.
(Enlarge)
The rules for reading and writing non-atomic locations are given by READ-NA and WRITE-NA. A thread can read an arbitrary element of the history of a non-atomic location, so long as the timestamp is greater than or equal to the timestamp in the thread’s frontier. A write to a non-atomic location by a thread must specify a timestamp later than that in the writing thread’s frontier.
Note a subtlety here: the timestamp need not be later than everything else in the history, merely later than any other write known to the writing thread.
The reduction rules for the small-step operational semantics operate on machine configurations consisting of a store S and a program P. A program is a finite set of threads, each with a frontier and an expression. Silent transitions are those that reduce expressions without involving memory operations. For transitions that involve memory (rule MEMORY), then the memory operation involved determines the thread’s new frontier and the new contents of the memory location.
A trace is a sequence of machine transitions starting from an initial state in which all locations have a timestamp 0. A trace is sequentially consistent if it contains no weak transitions. A weak transition is a machine step performing a memory operation at a non-atomic location where one of the following holds:
- the thread does not read the latest write to the location (reads a value with timestamp greater than its frontier, but not the very latest)
- the thread writes a value to the location with a timestamp greater than the thread’s frontier, but not greater than the largest timestamp in the location history (i.e., it is not the latest write to that location)
Two transitions conflict if they access the same atomic location and at least one is a write. If there is no happens-before relation between the two transitions then we have a data race. A happens-before relation can take one of two forms: either the transitions happen on the same thread, or the location involved is atomic and at least one of the transitions is a write.
If instead of considering the whole memory store we focus in on a subset of locations L, then a transition is L-sequential if it is not a weak transition, or if it is a weak transition but not on a location in L.
A machine is L-stable if all of the L-sequential transitions in its traces are data race free.
Intuitively, M is L-stable if there are no data races on L in progress when the program reaches state M. There may be data races before reaching M, and there may be data races after reaching M, but there are no data races between one operation before M and one operation afterwards.
From an L-stable machine M, the local DRF theorem tells us that we can reason locally over a set of transitions starting from M. If all of those transitions are L-sequential then the program is data race free through those transitions.
Mapping to hardware
To facilitate mapping the operational model defined above to hardware (x86 and ARMv8) the authors also define an axiomatic semantics in terms of read and write events. Events are generated during program execution and form an event graph G. Three binary relations are defined over events:
- program order (po): E1 po E2 if E1 and E2 occur on the same thread and E1 is ordered before E2 on that thread.
- reads from (rf): E2 rf E1 if E1 is a write event and E2 is a read event, and both events have the same location and value
- coherance (co): E1 co E2 if E1 and E2 are write events to the same location
In addition, a from-reads (fr) relation is defined in terms of rf and co. E1 fr E2 if E1 reads a value which is later overwritten by E2.
The axiomatic semantics are mapped to the operational semantics to show that they define the same memory model.
We now show that our memory model can be compiled efficiently to the x86 and ARMv8 memory models, and define the optimisations that are valid for a compiler to do… In our memory model, not all of the po relation is relevant, which is an important property for both compiler and hardware optimisations. For instance, there is no constraint that two nonatomic reads must be done in program order.
There are some constraints on program (re-)order(ing) though:
- operations must not be moved before prior atomic operations
- operations must must be moved after subsequent atomic writes
- prior reads must not be moved after subsequent writes
- conflicting operations must not be reordered.
These constraints still permit a number of peephole optimisations including:
- Sequentialisation:
[P || Q] => [P ; Q](which is surprisingly invalid under C++ and Java memory models) - Redundant load (elimination):
[r1 = a; r2 = a;] => [r1 = a; r2 = r1] - Store forwarding:
[a = x; r1 = a] => [a = x; r1 = x] - Dead store (elimination):
[a = x; a = y] => [a = y] - Common subexpression elimination:
[r1 = a*2; r2 = b; r3 = a*2] => [r1 = a*2; r3 = r1; r2 = b] - Loop-invariant code motion:
[while(...) { a = b; r1 = c*c; ...}] => [r2 = c*c; while(...) { a = b; r1 = r2; ... }] - Dead store elimination through reordering:
[a = 1; b = c; a = 2] => [b = c; a = 1; a = 2] => [b = c; a = 2] - Constant propagation via store forwarding:
[a = 1; b = c; r = a] => [b = c; a = 1; r = a] => [b = c; a = 1; r = 1]
Furthermore, if a program fragment satisfies the local DRF property, then the compiler is free to apply any optimisations valid for sequential programs, not just the ones permitted by the memory model, to that program fragment.
Compilation to x86 looks like this (with details in section 7.3 of the paper):
And compilation to ARMv8 is as follows (details in section 7.3 of the paper):
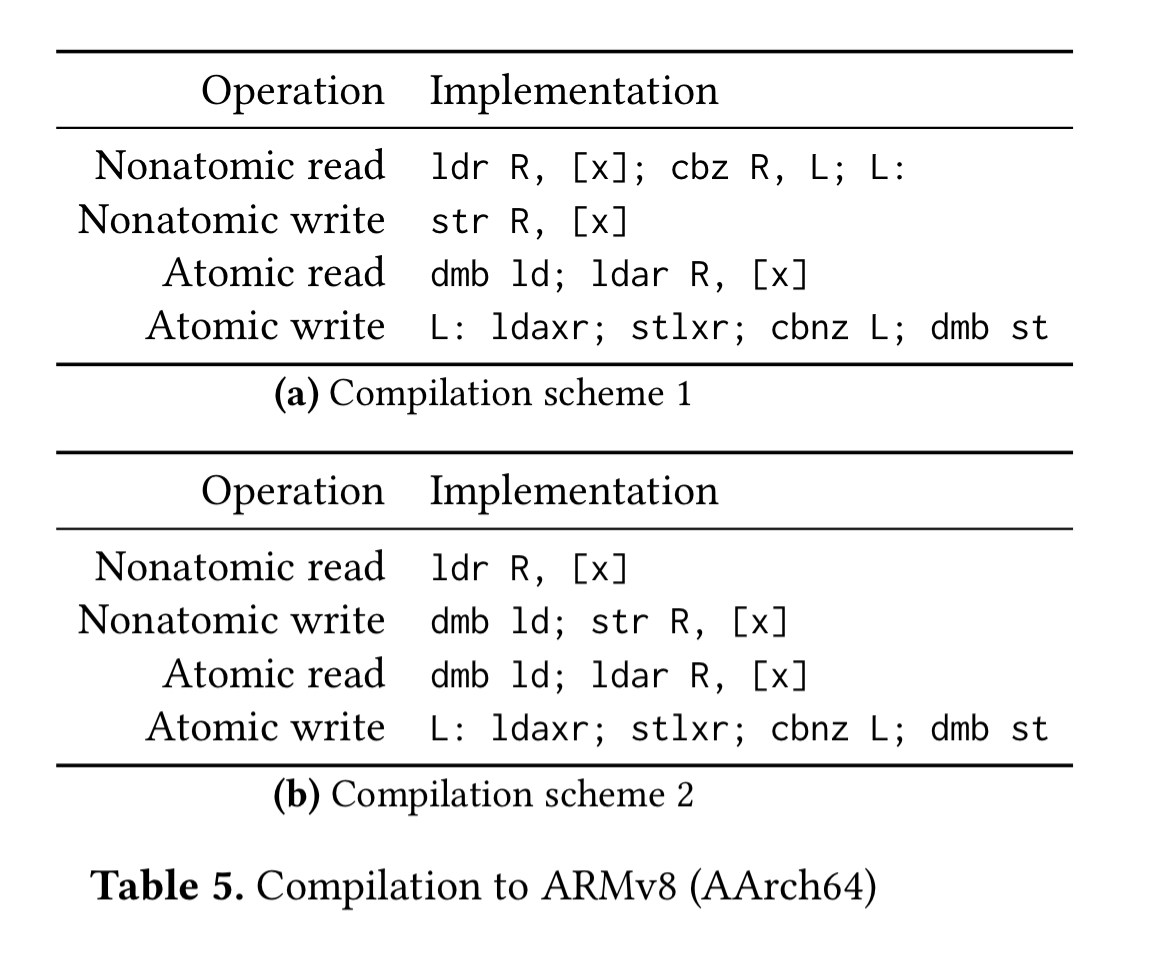
In all cases compilation is sound: every behaviour that the hardware model allows of a compiled program is allowed by the software model of the original program.
What price do we pay for local DRF?
We focus on quantifying the cost of nonatomic accesses on ARM and POWER architectures, since nonatomics in our memory model are free on x86. We leave the evaluation of the performance of our atomics for future work. Our aim is to evaluate the suitability of the memory model to be the default one in Multicore OCaml, a parallel extension of OCaml with thread-local minor heaps and shared major heap.
A suite of OCaml benchmarks are run looking at the overheads of the two ARMv8 compilation schemes (one using branch-after-load, and one using fence-before-store). The comparison also includes a strong release/acquire model which is strictly stronger than both.
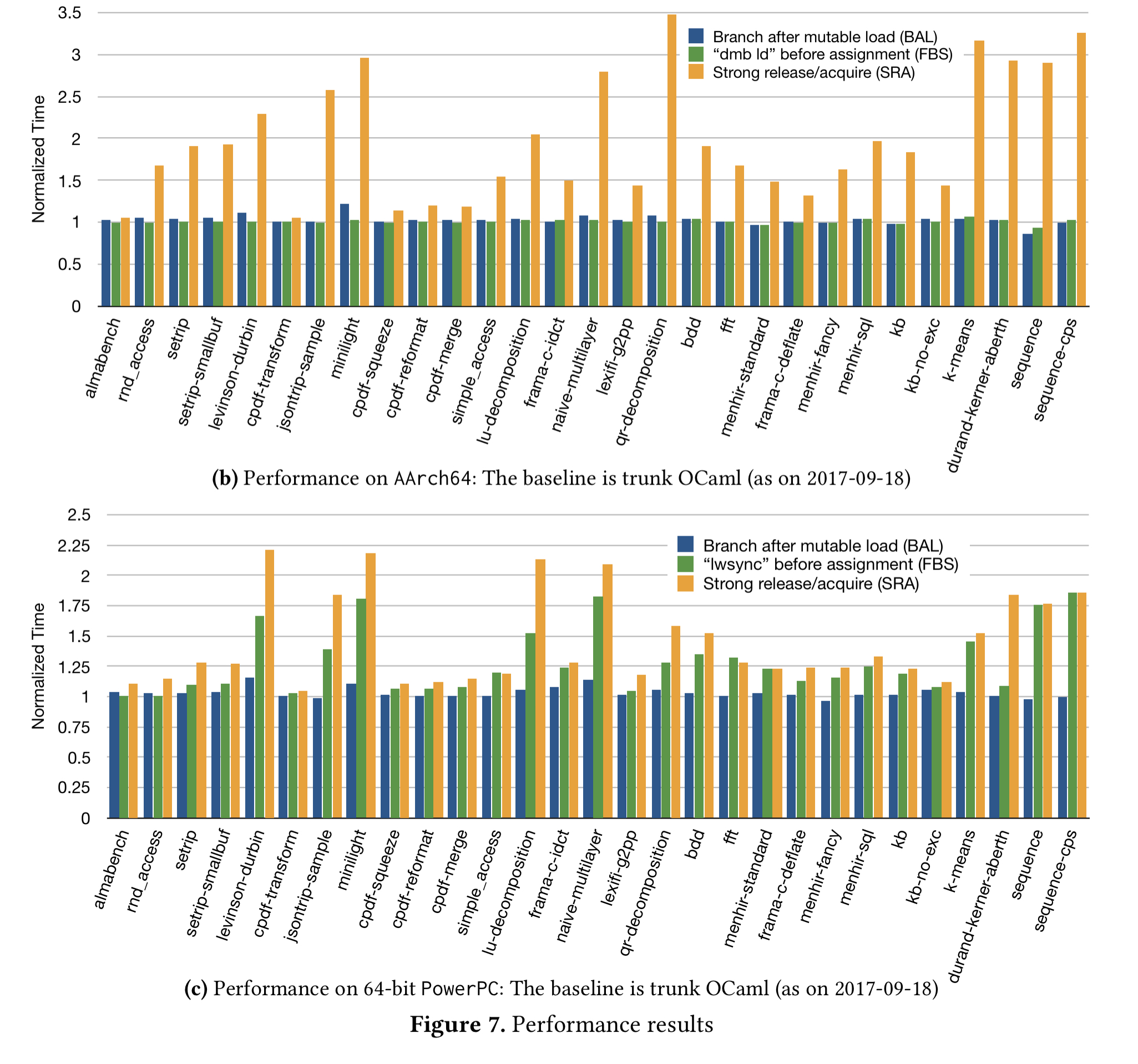
On average, branch-after-load is 2.5% slower than the (non-parallel) OCaml baseline, and fence-before-store is 0.6% slower.
Our memory model is simpler than prevalent mainstream models and enjoys strong reasoning principles even in the presence of data races, while remaining efficiently implementable even on relaxed architectures… In future work we plan to extend our currently spartan model with other types of atomics. In particular, release-acquire atomics would be a useful extension: they are strong enough to describe many parallel programming idioms, yet weak enough to be relatively cheaply implementable.