Improving the expressiveness of deep learning frameworks with recursion Jeong, Jeong et al., EuroSys’18
(If you don’t have ACM Digital Library access, the paper can be accessed either by following the link above directly from The Morning Paper blog site).
Last week we looked at the embedded dynamic control flow operators in TensorFlow. In today’s paper choice, Jeong et al. make the case for support of an additional control flow construct: recursion. A little recursion it turns out, can go a long way. Implemented on top of TensorFlow (and with a design that should also work for other embedded control flow machine learning frameworks e.g. Theano, Caffe, MXNet), support for recursion enables cleaner expression of a class of model architectures, and improved performance. The performance gains come from the increased opportunities to exploit parallelism within the recursive definitions.
In this paper, we introduce recursive definitions into the programming model of existing embedded control flow frameworks, adding first-class support for recursion. By allowing users to directly express recursive definitions in application code with enhanced programmability, models with recursive data structures such as trees or graphs can be written without requiring users to use a separate complex API to express the control flow. Also, optimization opportunities can be exploited to boost performance, such as concurrently executing child nodes in tree structures that have no dependencies between each other.
The case for recursion
If you have a naturally recursive model structure today, your choices are to translate the recursion into an iterative form, and potentially then also unroll the loop. This can be a non-trivial conversion process and lead to code with quite some conceptual distance from the design. Consider the case of a TreeLSTM:
TreeLSTM is a widely used recursive neural network based on LSTMs that is known to perform well for applications with tree-shaped data instances such as parse trees for natural language processing and hierarchical scene parsing.
As the name suggests, in a TreeLSTM, LSTM cells are combined to form a tree, often mimicking the shape of the input data tree. With only iterative control flow forms available, a TreeLSTM model must be encoded using loops. Here’s an example:

For the approach above to work, the input tree must be preprocessed so that its nodes are assigned with topologically sorted indices (i.e., it’s ok to process the nodes in iterative order). This process loses the parent-child relationships of the tree.
Since the recursive nature of the tree structure cannot be directly represented by iteration, it is difficult to write and understand this code… A recursive formulation, on the other hand, would be able to utilize the information on parent-child relationships to concurrently execute nodes, and is inherently more suitable for representing recursive neural networks, preserving their recursive nature.
SubGraphs and InvokeOps
Working with embedded control flow systems, it is clear that if we are to support recursion, we need to do it via operators in the dataflow graph. The first step is to provide a way of encapsulating and naming a subset of the computation graph (i.e., declaring a ‘function’). The authors call this unit of recursion a SubGraph. This encapsulation support is a powerful capability in its own right. Once we have a way of declaring a subgraph, we also need a way to invoke it, which is where InvokeOp comes in.
Here’s the TreeLSTM example rewritten as a recursive subgraph:

When creating a subgraph, any inputs and outputs of operations connected to outer operations (i.e., operations that fall outside of the subgraph) are bundled up as inputs and outputs of the SubGraph itself. During execution, the inputs are passed to the appropriate operations, and the outputs are shipped out as SubGraph outputs. SubGraphs may invoke other SubGraphs, including themselves.
The InvokeOp operation takes a set of tensors as input, runs an associated SubGraph with the provided inputs, and returns the resulting tensors as output.
InvokeOps are execution objects instantiated from SubGraph invocations; as SubGraphs are semantically close to function definitions, InvokeOps can be considered as function calls to the functions specified by SubGraphs.
In general an InvokeOp looks just like any other operation in the graph, except that instead of performing a mathematical calculation, it abstracts the execution of an entire SubGraph.
This difference also affects a process called automatic differentiation, a core functionality provided by modern deep learning frameworks for training models. Instead of calculating mathematical derivatives of some numerical function like other operations, the framework must take into account the associated SubGraph of an InvokeOp.
Automatic differentiation
The feedforward output of an InvokeOp is the execution output of its associated subgraph. Therefore the gradient of an InvokeOp can also be generated from the gradients of the associated subgraph. For a single invocation of a subgraph, we can collect the subgraph gradient operations inserted by automatic differentiation and add them to the backpropagation path. In the case of recursion though, we need to take care to track the gradients for inner recursive computations as well. The solution is to make a differentiation subgraph wrapping the gradient operations…
… we wrap each set of gradient operations from SubGraphs with yet another SubGraph. If a feedforward SubGraph contains a recursive invocation to itself, then its corresponding backpropagation SubGraph will also hold a recursive invocation, at the same position. Later, InvokeOps are inserted at SubGraph invocation points for both the feedforward SubGraph and the backpropagation SubGraph to complete the computation graph.
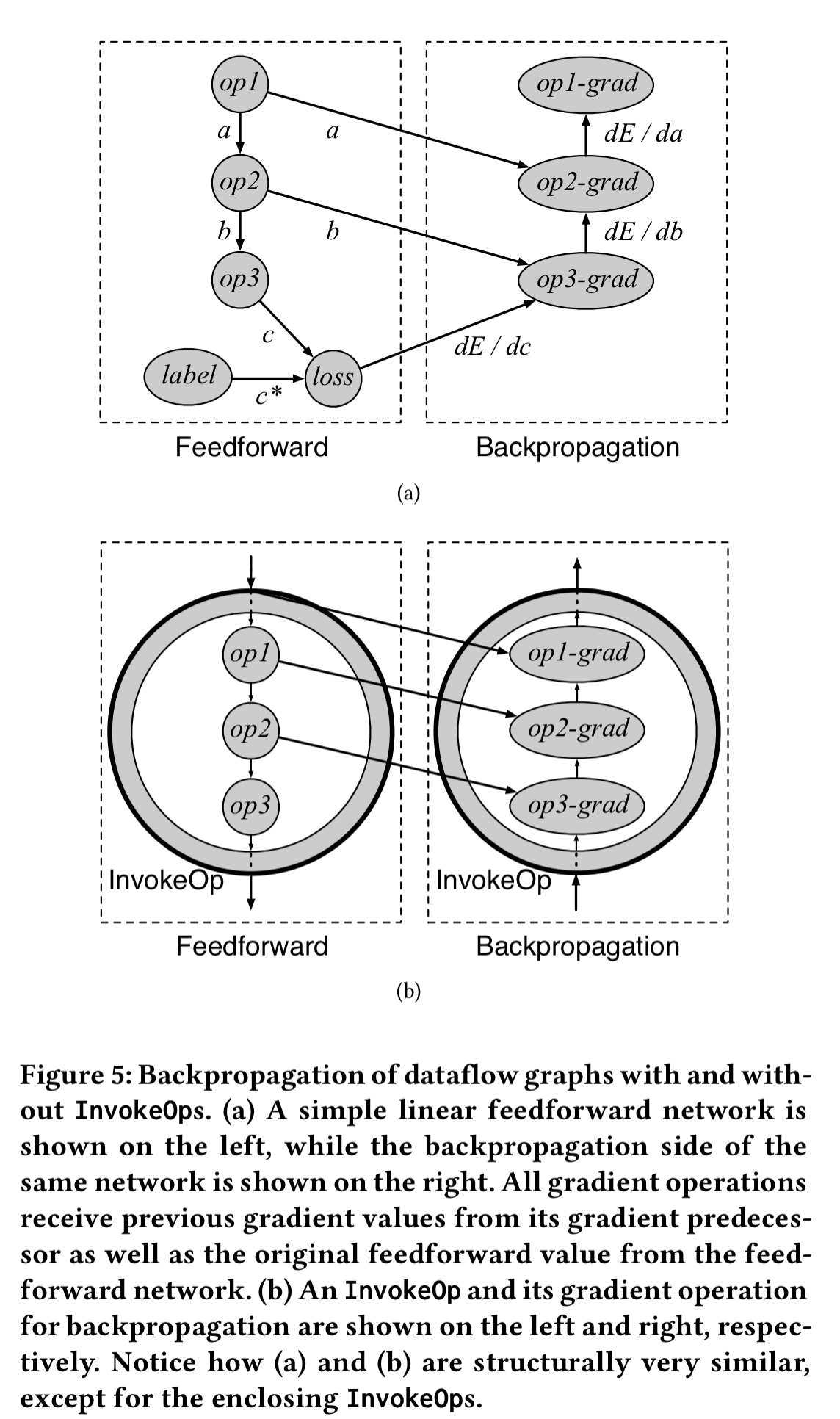
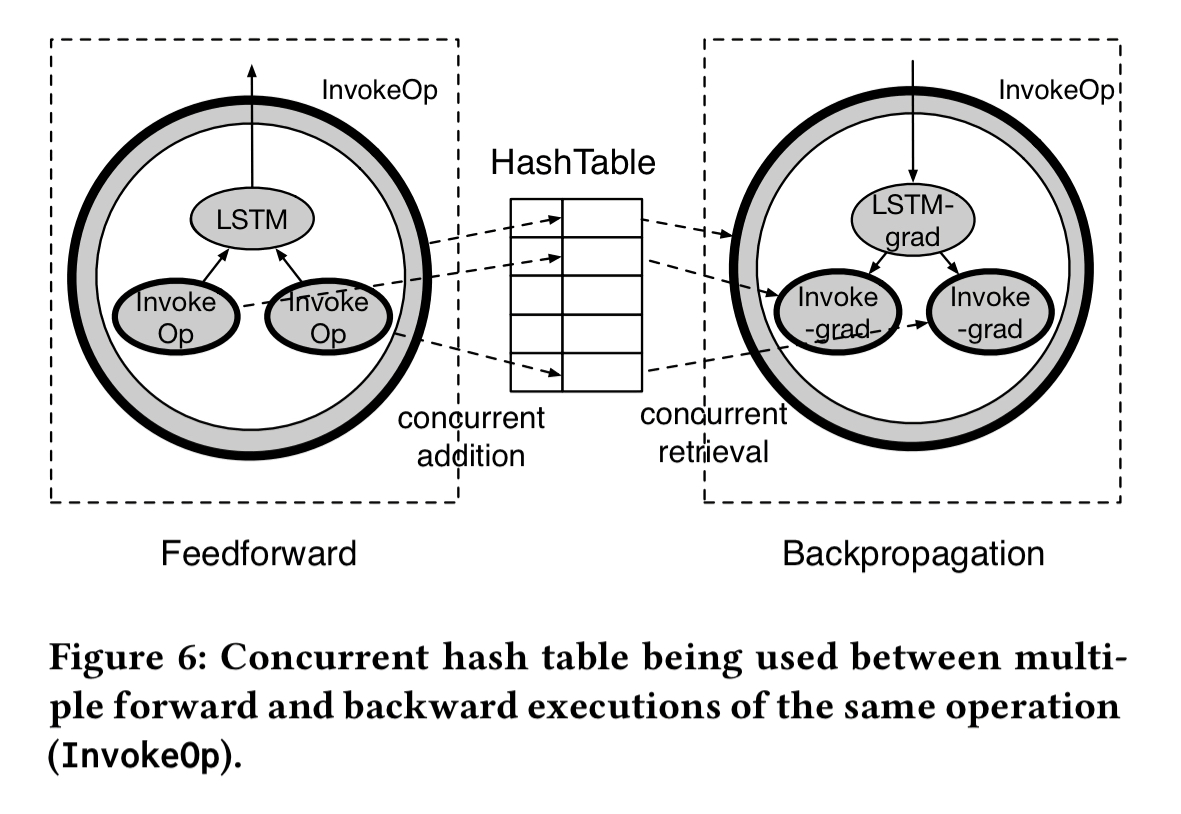
Recall that the output values of the feedforward phase are also fed into gradient operations, so we need to keep track of these. The implementation uses a concurrent hash table to store and fetch SubGraph outputs. Keys into the hash table are constructed based on the InvokeOp’s topological position within the SubGraph, combined with the key of the parent InvokeOp. During feedforward value are inserted into the hash table, and they are subsequently fetched during backpropagation.
Evaluation
The authors compare three different models (TreeRNN, RNTN, and TreeLSTM) trained using the Large Movie Review dataset. Each model is encoded in three ways: using the recursive constructs outlined in this paper, using iterative loops, and unrolled. Training was done with batch sizes of 1, 10, and 25.
Thanks to the parallelism exploited by recursive dataflow graphs, our implementation outperforms other implementations for the TreeRNN and RNTN models at all batch sizes, by up to 3.3x improved throughput over the iterative implementation, and 30.2x improved throughput over the static unrolling approach.
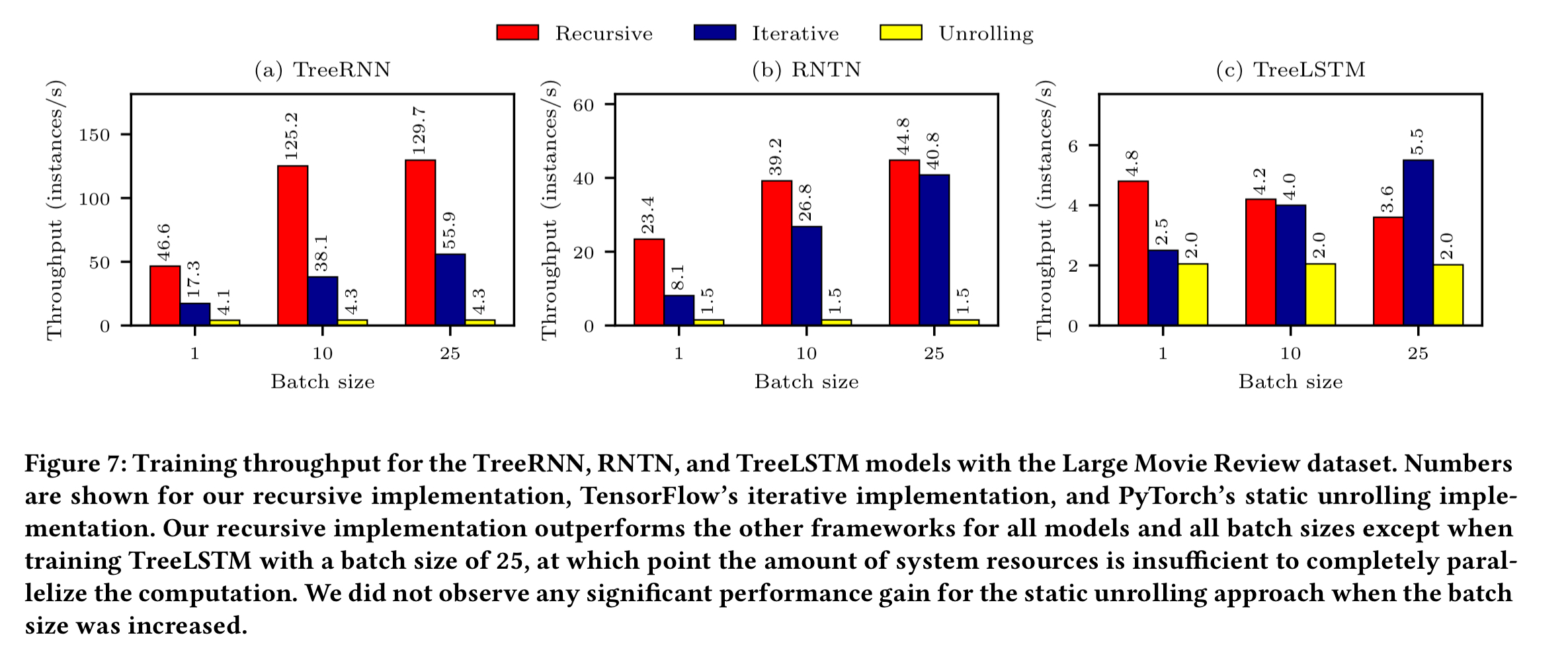
With the TreeLSTM model, recursion wins until we get to a batch size of 25, at which point iteration does better. The authors put this down to the high resource utilisation of the recursive implementation in backpropagation when computing large batches.
It’s also interesting to look at inference throughput (i.e., using the trained model to make predictions). This uses the feedforward phase, but no backpropagation. On inference, the recursive implementation wins across the board, with up to 5.4x throughput compared to iterative approaches, and 147.9x higher throughput compared to unrolling.
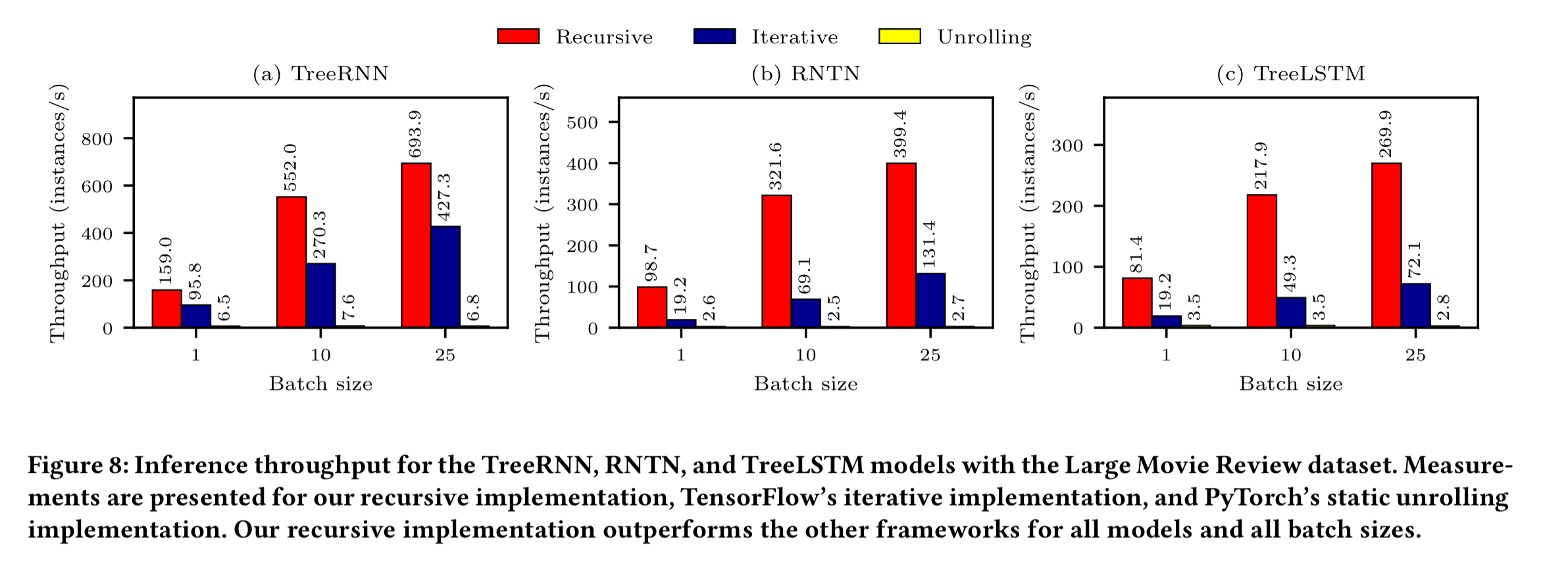
The performance difference between the iterative and recursive implementation of the same recursive neural network mainly comes from the parallelization of recursive operations.
In short, with the recursive implementation we have more opportunity to process tree cells concurrently, whereas the iterative approach can only process one cell at a time.