Quantum algorithms: an overview

~ Adrian Colyer

Quantum algorithms: an overview Montanaro,  npj Quantum Information 2016

This is a paper that Preskill cited in his keynote address (see yesterday’s post). It covers some of the same ground that we looked at yesterday, but also has some additional material and perspective of interest — and I’ll focus on those parts today. We’ll touch on Grover’s algorithm, amplitude amplification, and quantum walks among others. The first fun thing to know is that the Quantum Algorithm Zoo maintains a catalog of all known quantum algorithms – and there are a lot of them! For each algorithm you get the name, speedup, and a short description. A great resource. In ‘Quantum algorithms: an overview’, Montanaro offers a broad sweep of potential applications rather than details on how particular applications work. He also introduces us to a couple of complexity classes we haven’t seen before in The Morning Paper, BPP and QMA:

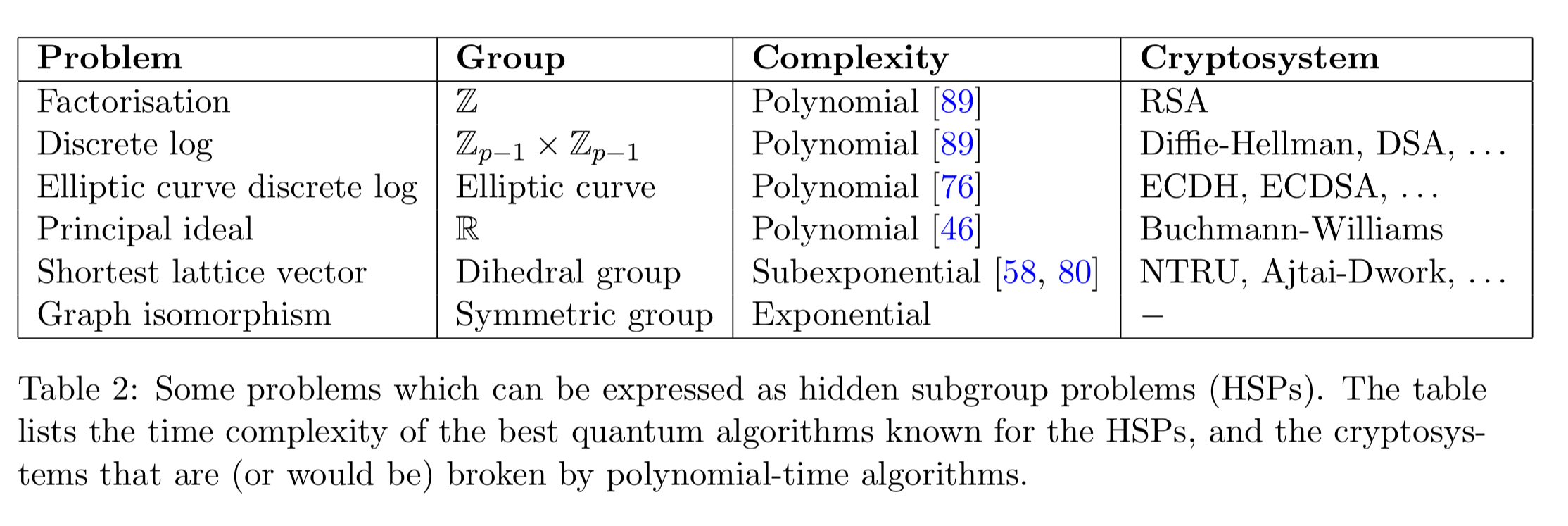
Shor’s algorithm, which we looked at last week, turns out to solve a special case of a mathematical problem known as the hidden subgroup problem (HSP).

For Shor’s algorithm, G = \mathbb{Z}. But if we use other groups G, the same quantum HSP algorithm can also attack other cryptosystems:

Grover’s algorithm

Beyond Shor’s algorithm, the best known quantum algorithm must be Grover’s algorithm. It’s a pretty amazing result for the unstructured search problem:

A classical algorithm must evaluate f 2^n times in the worst case, but Grover’s quantum algorithm solves the problem using O(\sqrt{N}) evaluations of f in the worst case. It is a bounded-error algorithm: it fails with probability \epsilon for some arbitrarily small (but fixed) \epsilon greater than 0. Grover’s algorithm does not rely on or exploit any internal structure in the function f.

Grover’s algorithm can be applied to any problem in the complexity class NP, since we can efficiently check if we have a solution in polynomial time (i.e., check whether f(x) = 1). In the following, we present a certificate which is a candidate proof of a solution, and the certificate can be verified in polynomial time:

Given a problem in NP that has a certificate length m, by applying Grover’s algorithm to A (the classical checking algorithm) and searching over all possible certificates, we obtain an algorithm which uses time O(2^{m/2}\ \mathrm{poly}(m)) rather than the O(2^m\ \mathrm{poly}(m)) used by classical exhaustive search over all certificates. This (nearly) quadratic speedup is less dramatic than the super-polynomial speedup achieved by Shor’s algorithm, but can still be rather substantial.

Amplitude amplification

The heuristic search problem is related to unstructured search, but starts with a probabilistic guessing algorithm to produce a guess which can then be tested:

The classical solution can find an answer in an average of O(1/\epsilon) evaluations of f, simply by repeatedly running A and checking the output each time. A quantum algorithm known as amplitude amplification, due to Brassard et al., can find w with only O(1/\sqrt{\epsilon}) uses of f, and a failure probability arbitrarily close to 0 — a quadratic speedup.

3-SAT is an NP-complete problem that runs in time O((4/3)^n \ \mathrm{poly}(n)). Applying amplitude amplification to the problem gives a quantum algorithm with runtime O((4/3)^{n/2} \ \mathrm{poly}(n)), “illustrating that quantum computers can speed-up non-trivial classical algorithms for NP-complete problems.”

Combinations…

Grover’s algorithm and amplitude amplification are powerful subroutines which can be used as part of more complicated quantum algorithms, allowing quantum speedups to be obtained for many other problems.

For example: finding the minimum of an unsorted list of N integers (quantum computers can do this in O(\sqrt{N})); determining graph connectivity, and pattern matching (find a pattern P of length M within a text T of length N).

If we can find the minimum of an unsorted list of N integers in O(\sqrt{N}), we can also find the minimum of an arbitrary and initially unknown function f : {0,1}^n \rightarrow \mathbb{Z} with O(\sqrt{N}) evaluations of f.

Adiabatic optimisation

The adiabatic optimisation algorithm can be applied to any constraint satisfaction problem (CSP) where we are given a sequence of constraints applied to some input bits, and are asked to output an assignment to the input bits which maximises the number of satisfied constraints…. Unlike the algorithms described in the rest of this survey, the adiabatic algorithm lacks general, rigorous worst-case upper bounds on its runtime.

The neat thing about the adiabatic algorithm is that we can directly implement it on a physical system whose Hamiltonian can be varied smoothly between the desired initial and final Hamiltonians. This is the approach taken by the D-Wave Systems machines.

Quantum walks

In classical computer science the concept of the random walk or Markov chain is a powerful algorithmic tool, and is often applied to search or sampling problems. Quantum walks provide a similarly powerful and general framework for designing fast quantum algorithms… a quantum walk is based on the simulated coherent quantum evolution of a particle moving on a graph.

Quantum walks can outperform classical random walks in two ways:

  1. faster hitting: the time it takes to find a target vertex from a source vertex (for some graphs, this time can be exponentially less), and
  2. faster mixing: the time taken to spread out over all vertices after starting from one source vertex. The mixing speedup can be quadratic, but no more than this.

One application of quantum walks is in fast evaluation of boolean formulae – a formula on N binary inputs can be evaluated in ‘slightly more than’ O(N^{1/2}) operations (vs O(N^{0.753...}) in the worst case for classical algorithms).

Quantum walks can also be used to obtain a very general speedup over classical algorithms based on Markov chains.

Why aren’t there more exponential speedups?

There are a number of instances of quadratic speedups, but comparatively fewer exponential speedups. Why is this?

One reason is that strong lower bounds have been proven on the power of quantum computation in the query complexity model, where one only considers the number of queries to the input as the measure of complexity… in order to achieve an exponential speedup over classical computation in the query complexity model there has to be a promise on the input, i.e., some possible inputs must be disallowed.

(This is the hidden structure that Shor’s algorithm successfully exploits for example).

Another observation is that many quantum algorithms seem to be composed of just a few common building blocks (e.g., quantum walks and the quantum Fourier transform). It turns out (van Dam) that any quantum circuit can be approximated using only Toffoli and Hadamard quantum gates. The first of these is a purely classical gate, the second is equivalent to the Fourier transform over the group \mathbb{Z}^2.

Thus any quantum algorithm whatsoever can be expressed as the use of quantum Fourier transforms interspersed with classical processing. (However, the intuition behind the quantum algorithms described above is much more varied than this observation would suggest).