Bolt: anonymous payment channels for decentralized currencies Green and Miers et al., CCS’17

Yesterday we spent some time looking at what payment channels are, their role in helping Bitcoin to scale by taking some of the load off of the chain, and some payment channels constructions such as direct channels, indirect channels via an intermediary, and event payment routing over a network of payment channels.

Today we’ll be digging into Blind Off-chain Lightweight Transactions (Bolt) themselves: a set of techniques for constructing privacy-preserving payment channels for a decentralized currency.

Upon receiving a payment from some customer, the merchant learns no information beyond the fact that a valid payment (of some known positive or negative value) has occurred on a channel that is open with them. The network learns only that a channel of some balance has been opened or closed.

An anonymous payment channel scheme (an APC scheme) is constructed out of four main building blocks:

1. Key generation (KeyGen) and initialisation (Init) algorithms which are used to open a channel and escrow the initial balance. Merchants generate long-lived key pairs for use across all customers, customers generate a key pair per channel. The Init algorithm is run by both customer and merchant, resulting in a set of channel tokens for each. The tokens are transmitted to the payment network, together with a transaction to escrow the backing funds.
2. The Establish and Pay protocols which activate an channel (one time) and transfer payments. These are run between the customer C and the merchant M off of the chain. If the parties disagree about initial channel balances during an Establish exchange then the channel will not be activated and either party can subsequently close the channel.
3. Means of closing a channel that is no longer needed: Refund which is algorithm run by a customer to initiate channel closure, and Refute, the corresponding algorithm run by a merchant.
4. The Resolve protocol run by the network, which takes an input the customer and/or merchant close tokens, and disperses the funds. If any of the closure messages fail to verify, the balance of the channel is granted to the opposing party.

(Enlarge)

There are three variations of the protocols, in order of increasing complexity these enable:

1. Unidirectional payment channels — a customer can pay a merchant, but there is no facility for payments in the other direction (e.g., refunds).
2. Bidirectional payment channels — permit funds to flow in both directions along the channel
3. Third-party payments — indirect channels in which parties A and B can transact via an intermediary I.

Unidirectional payment channels

Unidirectional payment channels are based on a compact e-cash scheme. Such schemes enable the escrowed amount in the payment channel to be divided up into B separate coins. Initially the customer owns all the coins, and ‘pays’ the merchant through coin transfer. When the channel is closed, the escrowed funds are dispersed in proportion to the number of coins held by the customer and the merchant at the time.

To initiate a channel, a customer transmits a wallet commitment to the payment network along with the escrow funds and an ephemeral public signature verification key. The customer can now engage in the establishment protocol with the merchant.

• The customer generates B coin spend transactions, together with non-interactive zero-knowledge proofs that each coin is tied to the wallet commitment.
• The customer encrypts each of these transactions using a symmetric encryption scheme. Every transaction is encrypted with a unique key, and the transactions are ordered such that the key for transaction is embedded in the ciphertext for transaction . The resulting ciphertexts are signed using the customer’s secret key, and transmitted to the merchant.

The chain of encryption keys linked in the spend transactions is exploited to give an efficient way of closing the channel. Suppose a customer wants to close a channel with remaining balance N. Let i.e., the ‘index’ of the first unused spend transaction in the chain. The customer now posts a signed close message to the network with the channel ID, , and — the key for the ciphertext. The merchant can use this key to decrypt that ciphertext, thus obtaining the key for the next ciphertext in the chain, and so on until the end of the chain is reached.

If the customer cheats by revealing and invalid decryption key, or if any ciphertext decrypts to an invalid coin, or if the resulting transactions indicate that she has double-spent any coin, the merchant can post indisputable evidence of this cheating to the network — which, to punish the customer, will grant the full channel balance to the merchant.

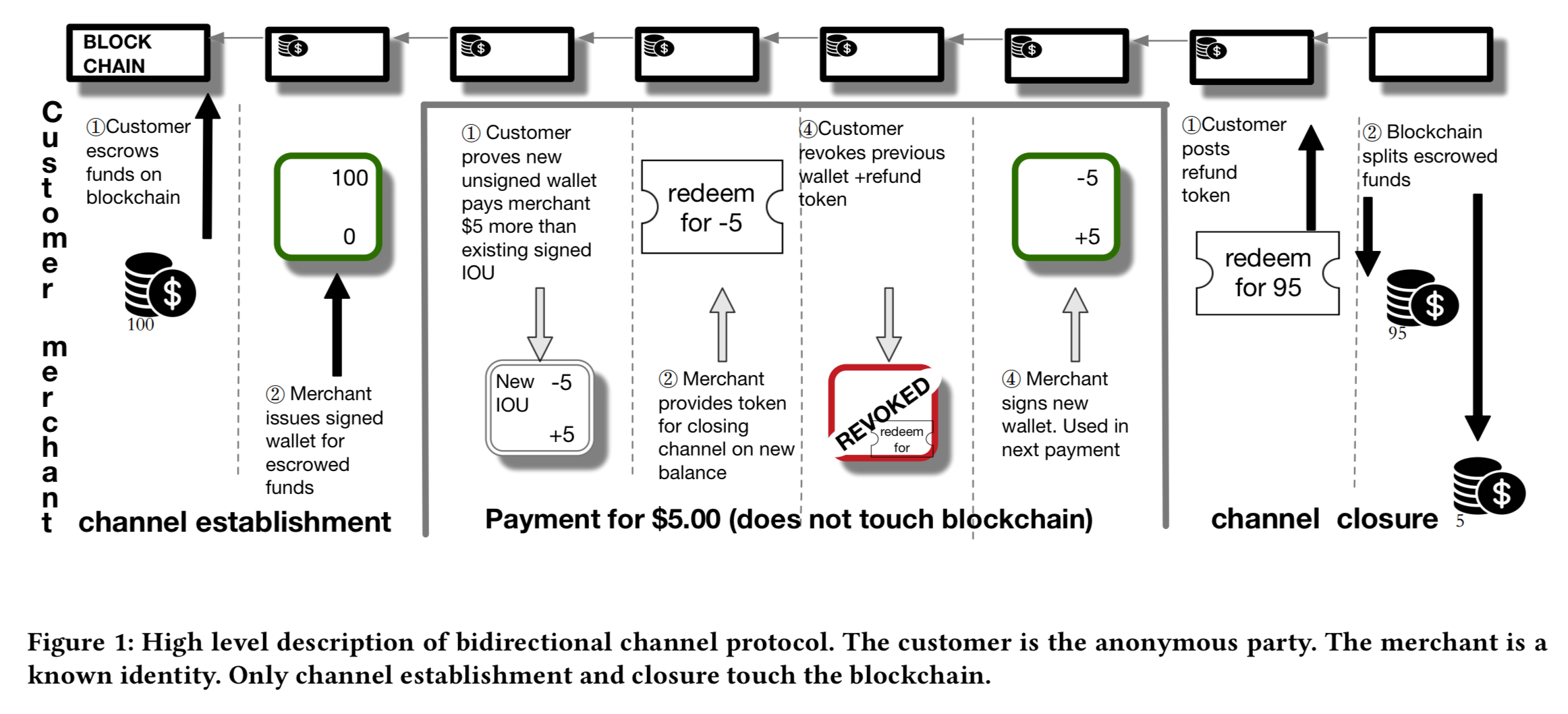
Bidirectional payment channels

Unidirectional channels support payments in only one direction, and only with fixed-value coins. The bidirectional channel construction allows payments in both directions, and the transfer of arbitrary values.

The key difference from the first protocol is that, instead of conducting the payment using a series of individual coins, each payment has the customer (1) prove that it has a valid signed wallet with balance of currency in it, and (2) request a blind signature on a new wallet for the amount (and embedding a fresh wallet public key ).

The value can be positive or negative. At the conclusion of the transaction, the customer reveals the public key of the old wallet to assure the merchant the wallet can’t be spent a second time, and the old wallet is also invalidate by the customer signing a “revoked” message. Closing a channel is done by posting a refund token signed by the merchant. End to end it looks like this:

(Enlarge)

Enabling third-party payments

One of the main applications of the bidirectional construction above is to enable third party payments. In these payments, a first party A makes a payment of some positive value to a second party B via some intermediary I with whom both A and B act as the customer for channel establishment, and I plays the role of the merchant.

The intermediary learns neither the identity of the participants, nor the amount being transferred. Nor does the intermediary need to be trusted to safeguard the participants funds. (Which is a pretty interesting set of properties when you think about it!).

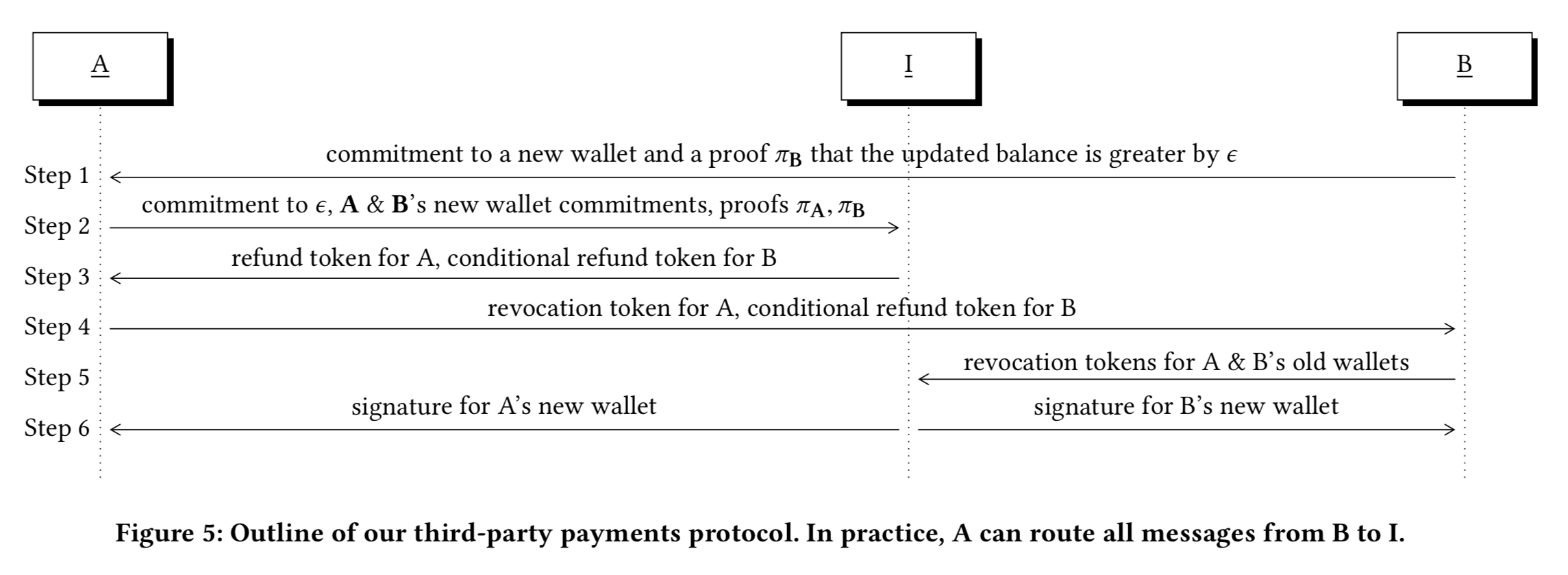
The payer A doesn’t want to pay the intermediary until the intermediary has paid B, but likewise the intermediary doesn’t want to pay B until funds from A have been received. “There is no purely cryptographic solution to this problem… however there are known techniques for using blockchains to mediate aborts.”

The first phase of the Pay protocol generates refund tokens that can be used to reclaim escrowed funds. For a chained transaction from A-I-B to be secure, it is enough that this first phase of both legs completes or fails atomically. To prevent B from claiming funds from I without a corresponding payment from A, then we add two conditions to B’s refund token:

1. B must produce a revocation message on A’s previous wallet. This prevents a payment from A to I being reversed once B forces a payment.
2. A must not have posted a revocation token containing the wallet key to the ledger. This prevents B forcing a payment if the payment from A to I has been reversed.

To hide the payment amount , instead of revealing it to the intermediary, the customer A now commits to and uses this value as a secret input in computing the payment.

End to end the payments protocol looks like this:

(Enlarge)

It’s possible to extend this protocol to allow payments that route through multiple intermediaries, but it is not possible to hide channel balances in such a setting.

The general approach is as follows: we use “hash locks” to enforce that either all refund and revocation tokens are valid or none are. Specifically, we attach to both the fund and revocation tokens a condition that they can only be used if one party reveals such that , where is picked by A. Because if one party releases , all parties may close their channels, this forces the entire sequence of payments to either go through or not. As with Lightning, the timeouts for each channel must be carefully chosen…