Popularity prediction of Facebook videos for higher quality streaming Tang et al., USENIX ATC’17
Suppose I could grant you access to a clairvoyance service, which could make one class of predictions about your business for you with perfect accuracy. What would you want to know, and what difference would knowing that make to your business? (For example, in the VC world you’d want to know which companies are going to make it big — that’s a hard one!). In many cases though, although perfect clairvoyance isn’t achievable, with some care and attention to data collection and modelling, you can get predictions that are useful.
Today’s paper looks at the problem of predicting the popularity of videos on Facebook. Why does that matter? As we saw yesterday, videos can be encoded at multiple different bitrates. Having a broader choice of bitrates means a better overall experience for clients across a range of bandwidths, at the expense of more resources consumed on the server side in encoding. In addition, Facebook’s QuickFire engine can produce versions of a video with the same quality but approximately 20% smaller than the standard encoding. It uses up to 20x the computation to do so though! Since video popularity on Facebook follows a power law, accurate identification of e.g. the top 1% of videos would cover 83% of the total video watch time, and allow us to expend server side effort where it will have the most impact.
The challenge in exploiting this insight is in scalably and accurately predicting the videos that will become popular. State of the art popularity prediction algorithms are accurate but do not scale to handle the Facebook video workload… Simple heuristics that exploit information from the social network scale, but are not accurate.
Facebook’s solution to this problem is CHESS: a Constant History, Exponential kernels, and Social Signals popularity prediction algorithm. Impressively, CHESS requires only four machines to provide popularity prediction for all of Facebook’s videos.
Compared to the heuristic currently used in production, CHESS improves the watch time coverage of QuickFire by 8%-30% using the same CPU resources for re-encoding. To cover 80% of watch time, CHESS reduces the overhead from 54% to 17%.
CHESS aligns with another theme of our times too. Whereas previous work on video popularity considered popularity on a daily (batch) basis, CHESS is able to make predictions quickly (on the order of minutes). This matters because if prediction takes longer than the interval between when a video is uploaded and when it peaks then much of the watch time will already be in the past by the time we figure out it would have been worth optimising.
So in summary we have scalable near-real time predictions to guide business decisions. Although CHESS has been applied here in a video context, the fundamental approach should generalize to predict popularity in other settings too.
Let’s jump straight into looking at the details of the CHESS prediction algorithm.
How the CHESS prediction algorithm works
A common theme in popularity prediction is exploiting past access patterns. The state of the art approaches do so by modeling the behavior as a self-exciting process that predicts future accesses based on all past accesses. A past access at time
is assumed to provide some influence on future popularity at time
, as modeled by a kernel function
.
Such self-exciting processes are based on the sum of the influence off all past requests from the current time to infinity. Power-law based kernels provide high accuracy predictions but require each new prediction to compute over all past accesses. Which in turn means linear growth of storage and computation with respect to past accesses. At the heart of CHESS is a new exponentially decaying kernel:
where represents a time window modelling how far into the future the influence of past requests extends.
Such a kernel allows us to simplify the computation of a new prediction to only require the last prediction,
, and its timestamp,
, which drastically reduces the space and time overhead.
Such an exponentially decayed watch time (EDWT) kernel is efficiently computable, but a weaker predictor than self-exciting processes with more powerful kernels.
We overcome this limitation of EDWTs with the second key insight in the CHESS design: combining many weak, but readily computable, signals through a learning framework achieves high accuracy while remaining efficient.
The learning framework is a neural network, and it’s refreshingly simple! The authors use a 2-layer network with 100 hidden nodes. Compared to linear models, using such a network reduces prediction error by 40%, but there was no further gain in moving to more complex network models. The inputs to the network are a combination of static and dynamic features. The static (stateless) features do not change dramatically during the life-cycle of a video – for example, the number of friends of the video owner, as well as things like the length of the video. The dynamic (stateful) features do change, and therefore we need state to track them. This include things such as the number of comments, likes, shares, saves, and so on. To keep the state constant per video, four exponential kernels with different time windows are used: 1, 4, 16, and 64 hours.
Values for some of the features can vary over a very wide scale: from 10-10^8 depending on video popularity.
Although linear scaling, in the form of standardization, is the commonly used method in statistical learning, we find that logarithmic scaling, i.e.,
, delivers much better performance for our workload.
Logarithmic scaling improves the coverage ratio of QuickFire by as much as 6% over linear scaling.
To generate training examples the authors use an example queue. The current state of a video is appended to the queue when it is accessed, and while it remains in the queue the watch time and feature values are tracked. After a prediction horizon amount of time has expired, the video is evicted from the queue again. A prediction horizon of six days is empirically found to give a good tradeoff between high accuracy and low overhead. To avoid the example queue being flooded by data points from the most popular videos, an additional constraint is that an example for a video is only admitted to the queue if at least D = 2 hours of time has elapsed singe the last example of the same video.
Putting it all together: the CHESS video prediction service
The CHESS video prediction service (CHESS-VPS) uses 8 workers distributed across 4 machines to generate predictions on the full Facebook workload.
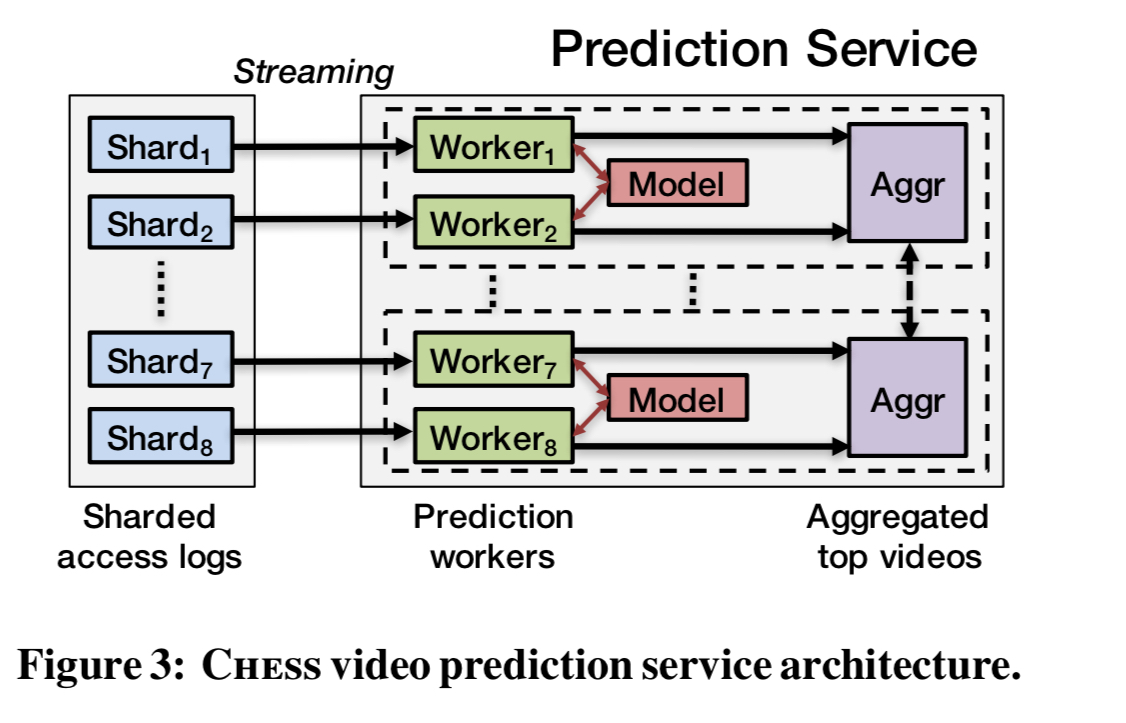
Facebook video accesses are logged to Scribe, and from there they are streamed to CHESS-VPS and sharded based on video ID into eight shards. Each worker queries TAO for the additional features that are needed. Queries are batched, and the results are cached for 10 minutes to reduce load. Workers maintain tables with their most recent predictions for the top 10 million most popular videos in its shard. Thus across the 8 shards there are 80 million videos that make up actively accessed video working set.
Every ten minutes each worker scans its table and sorts videos based on their predictions. An aggregator in each machine collects the top 1 million videos from the workers on that machine, and broadcasts these to all aggregators and waits for their predictions. When all the predictions have been received these are merged and sorted. These predictions are then used to answer queries for the next ten minutes.
Each video has 12 stateless features and 7 stateful features. These features, associated metadata, and current popularity prediction add up to a storage overhead of ~250 bytes per video. Thus, all 80 million videos use ~20GB RAM in total to maintain. This results in a total memory overhead of ~44GB RAM from models and metadata, or only ~11GB RAM per machine.