A model for reasoning about JavaScript promises

A model for reasoning about JavaScript promises§ Madsen et al., OOPSLA’17

As an antidote to callback-hell, ECMAScript 6 introduces Promises. Promises represent the value of an asynchronous computation, and the functions resolve and reject are used to settle the promise. Promises can be chained using then.

However, the semantics of JavaScript promises are quite complex, and since the feature is implemented by way of ordinary function calls, there are no static checks to ensure correct usage. As a result, programmers often make mistakes in promise-based code that leads to pernicious errors, as is evident from many reported issues on forums such as StackOverflow.

This paper introduces the notion of a promise graph, which can be used to visualise the flow in a promises-based program and help to detect a range of bugs. In order to have formal basis for such reasoning and program analysis the paper also introduces $\lambda_p$ , a calculus for the behaviour of promises, which is expressed as an extension to $\lambda_{JS}$ .

Promises essentials

A promise is an object that represents the result of an asynchronous operation.

A promise can be in one of three different states. Initially a promise is Pending, indicating that the operation has not yet completed and the promise holds no value. A Fulfilled promise is one in which the operation has succeeded and the promise holds a result value. A Rejected promise is one in which the operation has failed and the promise holds an error value. A promise that is either fulfilled or rejected is said to be settled.

A promise is constructed by passing a single callback function with two parameters: a resolve function that can be called to fulfil the promise, and a reject function that can be called to reject the promise. These parameters are named resolve and reject by convention.

[code lannguage=”javascript”]
var p = new Promise((resolve, reject) => {
resolve(42); // immediate resolution
});
[/code]

The then function can be used to register resolve reactions and reject reactions with promises, and creates in turn a dependent promise with the result computed by the resolve (reject) reaction.

Promises calculus

Section 3 of the paper defines a formal $\lambda_p$ calculus for all of this. The runtime state has five components:

A heap $\sigma$ that maps addresses to values
A promise state map $\psi$ that maps addresses to promise values (Pending, Fulfilled(value), or Rejected(value)).
A map $f$ that maps addresses to a list of fulfil reactions
A map $r$ that maps addresses to a list of reject reactions
And a queue $\pi$ that holds scheduled reactions – promised that have been settled and their reactions are awaiting asynchronous execution by the event loop.

A promisify expression in this language turns an object into a promise. Then there a bunch of reduction rules such as this one:

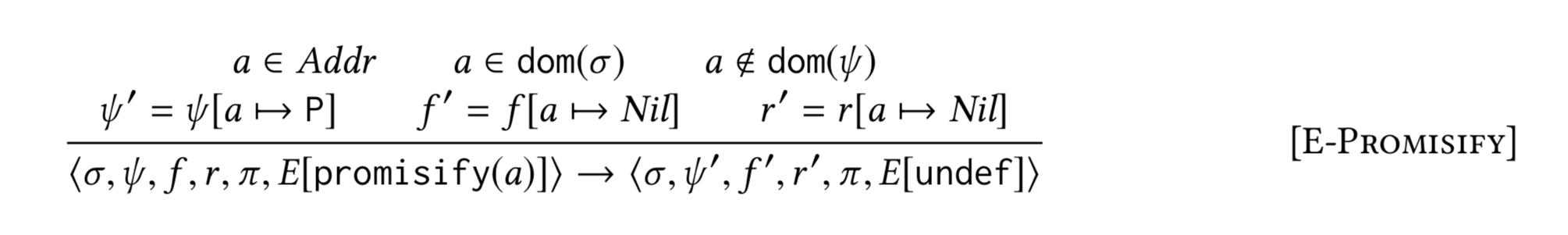
They can look a bit intimidating on first glance, but that’s mostly down to the syntax. For example, all this one says is that:

given $a$ is an address in the heap, that is not currently mapped to promise values, and an expression promisify(a)
then the system reduces to a new state where the expression value becomes undefined (the return value of a promisify expression),
and the promise state map is updated with a new entry for this address that holds the value Pending, the fulfil reaction and reject reaction maps get an empty entry for the address, and the rest of the state of the system is unaltered

The fun part of the paper for me though, is what happens when you create promise graphs off of the back of this formalism. So let’s get straight into that…

Promise graphs

The promise graph captures control- and dataflow in a promise-based program to represent the flow of values through promises, the execution of fulfil and reject reactions, and the dependencies between reactions and promises.

Promise graphs contain three different types of nodes:

Value nodes represent value allocation sites in the program
Promise nodes represent promise allocation sites in the program,
Function nodes represent every lambda or named function in the program.

There are four different types of edges between nodes as well:

A settlement edge (which can be labelled either ‘resolve’ or ‘reject’) from a value node $v$ to a promise node $p$ indicates that the value $v$ is used to resolve or reject the promise $p$ .
A registration edge (with label ‘resolve’ or ‘reject’) from a promise node $p$ to a function node $f$ indicates that the function $f$ is registered as a fulfil or reject reaction on the promise $p$ .
A link edge from a promise $p_1$ to a dependent promise $p_2$ represents the dependency that when the parent promise $p_1$ is resolved or rejected, the dependent promise will be resolved or rejected with the same value.
A return edge from a function node $f$ to a value node $v$ represents the function $f$ returning the value allocated at $v$ .

In the examples that follow, the subscript numbers (e.g., $v_{21}$ indicate the line number in the program on which the corresponding object is declared. At this point on first read I admit to thinking it would be easier just to read the code, but bear with me, it will all make more sense very soon.

Here’s a small example of a program and its corresponding promise graph:

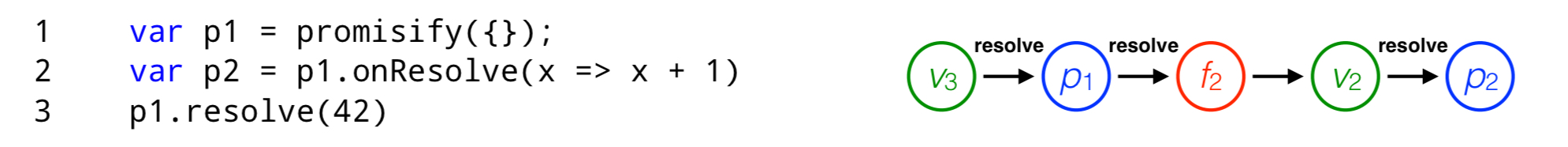
You can read the graph forward: the value on line 3 (42) is used to resolve the promise declared on line 1 (p1), and flows into the fulfil reaction function declared on line 2. Inside that function, the newly computed value ($v_2$) is then used to resolve the second promise $p_2$ . You can also read it backwards to trace the resolution of $p_2$ to understand how and why it was resolved.

Here’s an example with branching:

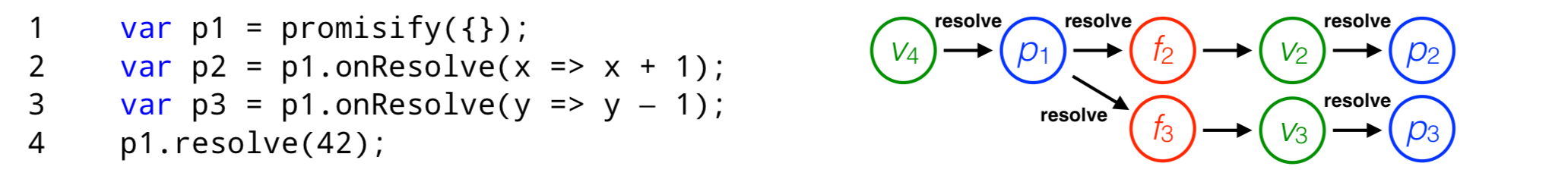
A real world example

Here’s some code from a StackOverflow question (Q42408234) and it’s corresponding promise graph. The poster had spend a full two hours trying to figure out why the promise from mongoose.find (on line 15) was returning undefined.

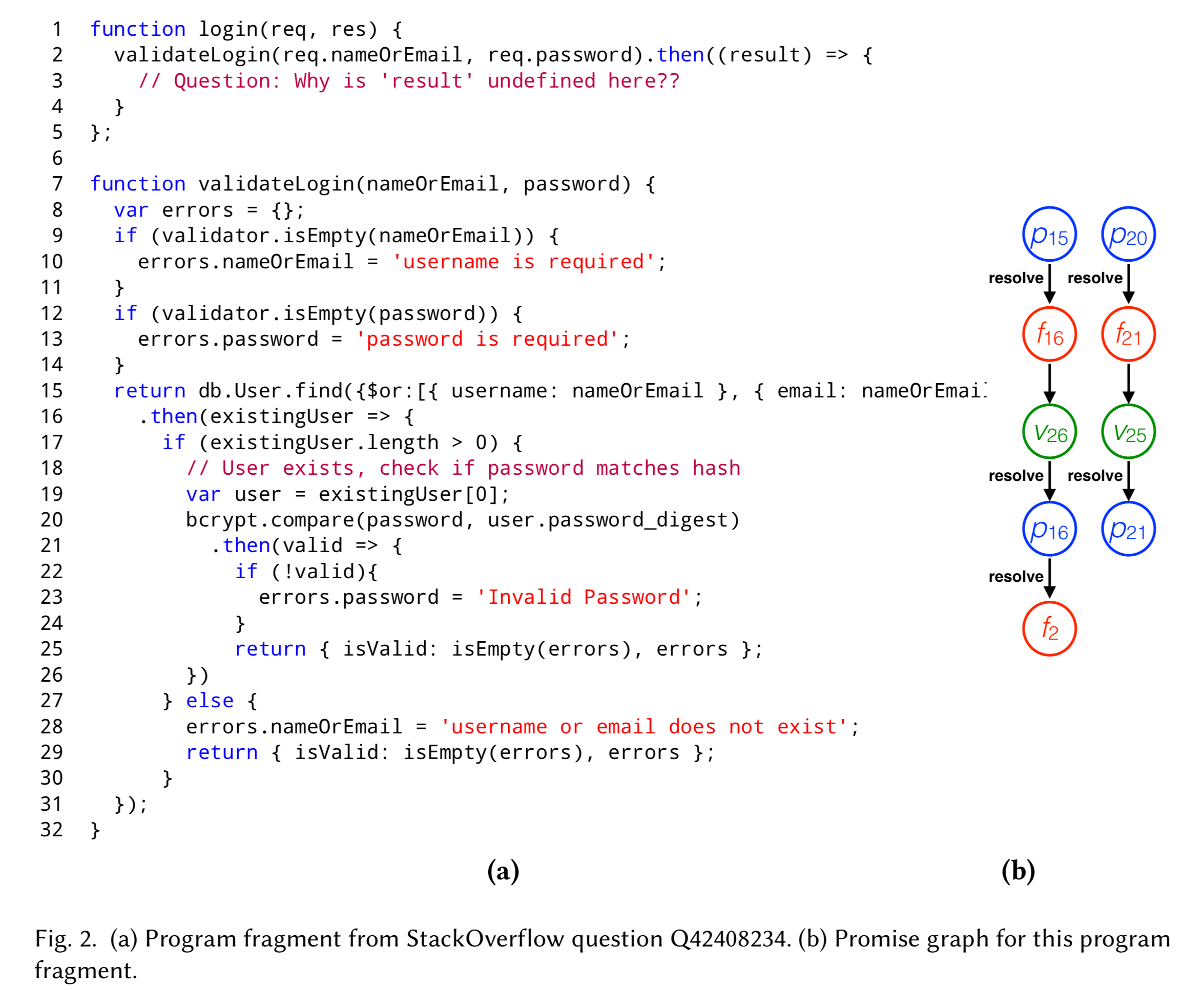
Immediately the promise graph shows us two disconnected chains. The value returned on line 25 is used to resolve the promise on line 21, but then doesn’t go anywhere else. The function declared on lines 16-31 does not explicity return a value, so it will implicitly return undefined. The fix is to explicitly return the the value of bcrypt.compare as computed on line 20.

A catalog of Promise-related bugs

Armed with the ability to create promise graphs, we can now detected a variety of promise-related bugs.

A Dead Promise occurs when an object enters the Pending state and never transitions to either a fulfil or reject state. A promise node with no resolve, reject, or link edges is dead.

A Missing resolve or reject reaction occurs when a promise is resolved with a non-undefined value, and the promise lacks a fulfil (or reject) reaction. This is a promise node with no outgoing edges.

A Missing exceptional reject reaction occurs when a promise is implicitly rejected by throwing an exception. These are promise nodes with a reject edge, but to reject registration edge.

A Missing return occurs when a fulfil or reject reaction unintentionally returns undefined and this value is used to resolve or reject a dependent promise.

A Double resolve or reject occurs when a promise enters the fulfilled or rejected state, and later the promise is again resolved (or rejected). This can be detected in the graph by multiple resolve (or reject) edges leading to the same promise.

An Unnecessary promise is a promise whose sole purpose is to act as an intermediary between two other promises.

A Broken promise chain occurs when a programmer inadvertently creates a fork in a promise chain.

Promise graphs and StackOverflow

The authors looked at the most recent 600 StackOverflow questions tagged with both promise and javascript (out of over 5,000 total). They focused on those with code fragments of at most 100 lines, a genuine promises-related issue, and an answer. This boiled things down to quite a small list, show below:

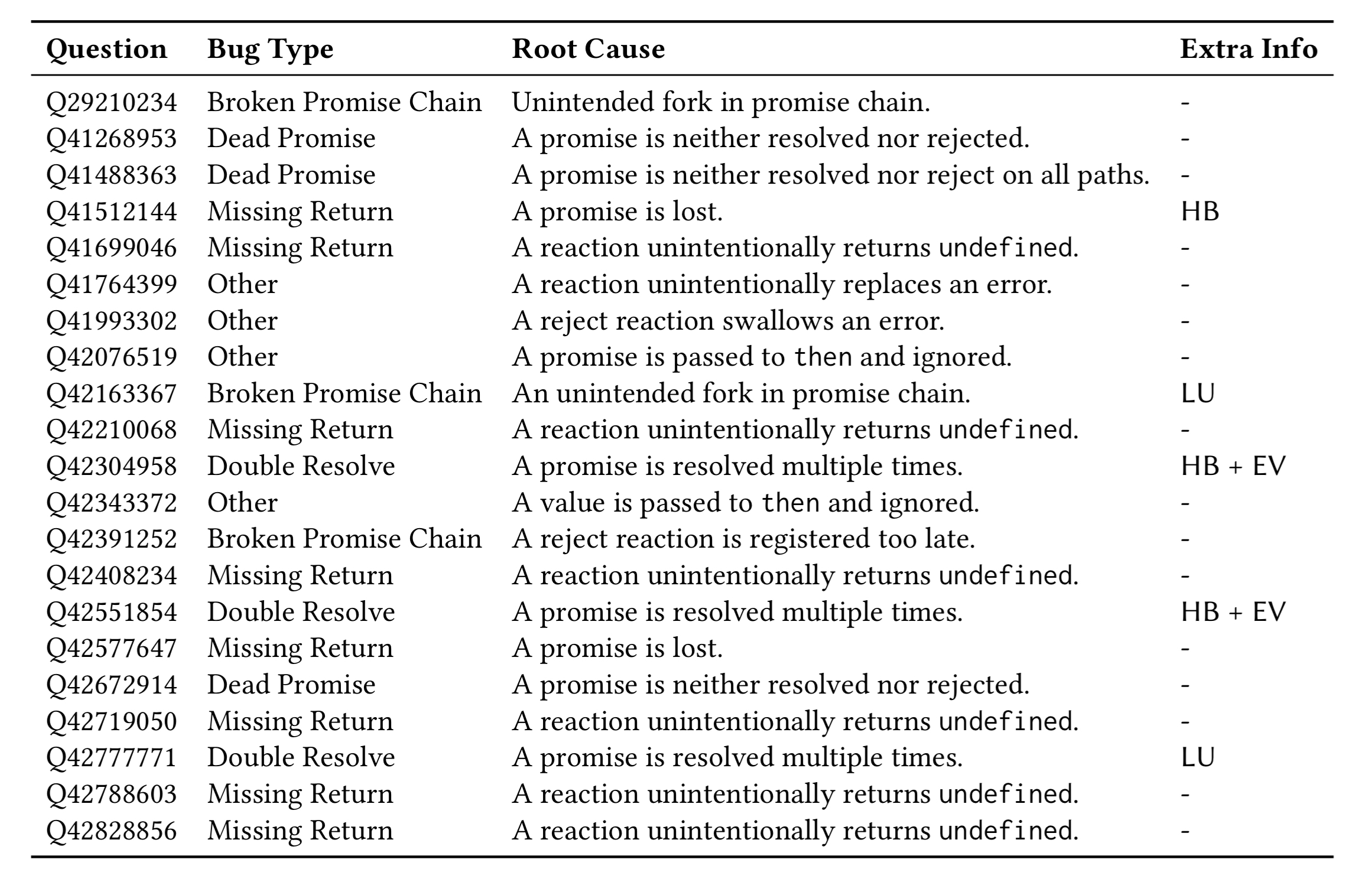
The fourth column in the table above shows the additional information — above and beyond the promise graph — that was needed to pinpoint the bug (if any).

HB indicates that happens-before information is needed – i.e., the knowledge that one statement in the program always executes before another.
LU indicates that loop unrolling is necessary to debug the root cause (i.e., what happens in one iteration affects a promise created in a subsequent one).
EV indicates that event reasoning is needed to debug the root cause – e.g., the knowledge that an event handler for a button can fire multiple times.

Here’s an example analysis:

Q41268953. The programmer creates a promise, but never resolves or rejects it. As a result, the reactions associated with the promise are never executed. The programmer gets lost in the details and mistakenly believes the bug to be elsewhere in the program. He or she then proceeds to add additional logging and reject reactions in all the wrong places and these are never executed. In this scenario, the promise graph immediately identifies that the initial promise in the promise chain is never resolved or rejected, and hence that no reaction on chain is ever executed.

There are plenty more examples in section 5.3, and in appendix A.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic