Log20: Fully automated optimal placement of log printing statements under specified overhead threshold

Log20: Fully automated optimal placement of log printing statements under specified overhead threshold Zhao et al., SOSP’17

Logging has become an overloaded term. In this paper logging is used in the context of recording information about the execution of a piece of software, for the purposes of aiding troubleshooting. For these kind of logging statements there always seem to be a trade-off between log verbosity, logging overhead, and the log actually containing enough useful information to help you diagnose a problem that occurs in the wild. As developers of the system, we tend to put logging statements in places where we think they’ll be useful – often as a retrospective action after a problem occurred that couldn’t easily be diagnosed!

So it’s interesting to step back for a moment and consider this: if you were starting to instrument a system from scratch, what would an optimal set of logging statements look like? Where would you place those statements and what criteria would you use to decide? If we assume great filtering and searching tools such that log verbosity is less of an issue, then a strawman would be to log every possible branch of execution. That’s optimal from the perspective of having the information needed in the log in order to diagnose any given problem. But we don’t do that because the performance overhead would be unacceptable. This gives us a clue for reframing the problem: what is the most useful information to log given a maximum logging overhead constraint?

This paper presents Log20, a tool that determines a near optimal placement of log printing statements under the constraint of adding less than a specified amount of performance overhead. Log20 does this in an automated way without any human involvement.

Throughout the paper, the abbreviation LPS is used to refer to a Log Printing Statement.

Logging the manual way

Here’s an analysis of the number of LPSes at different severity levels in Cassandra, Hadoop, HBase, and ZooKeeper, indicating that developers seem to find plenty of value in recording non-error information in addition to error conditions:

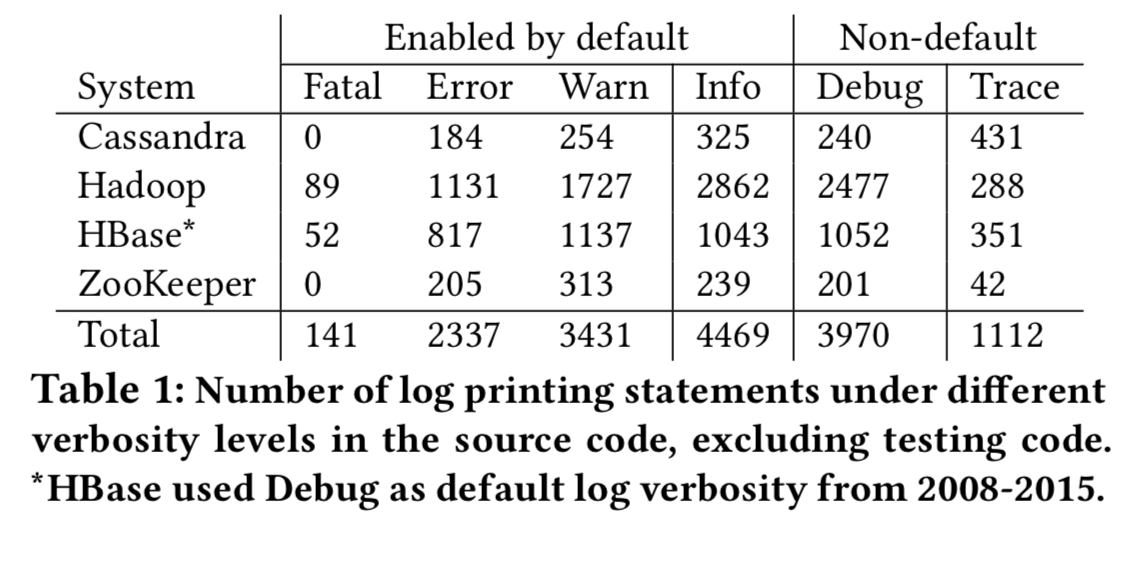
Looking at the revision history of these systems, and following some of the discussion in bug reports, reveals that:

Logging statements are often added retrospectively – 21,642 revisions have the sole purpose of adding log statements, presumably after finding they were needed to diagnose a problem.
Balancing information and overhead is hard – at what level should a given piece of information be logged? Battles rage back and forth on this in comment threads (and commits!). 2,105 commits only modify a severity level.
Setting the right verbosity level is also hard subjectively – whether something is an Error or Info for example can depend on the particular workload.

How much information is that set of log statements providing?

The first and most significant puzzle piece on the journey towards optimal logging is figuring out how much information we’re getting from a particular log statement. Given the placement of a set of logging statements, the authors use an entropy-based model to capture the amount of uncertainty (unpredictability) that remains in figuring out which execution path was taken. We want to place log statements in such a way that entropy is minimised.

Log20 considers execution paths at the block level. That is, an execution path is a sequence of the blocks that the system traversed at runtime. Consider this program:

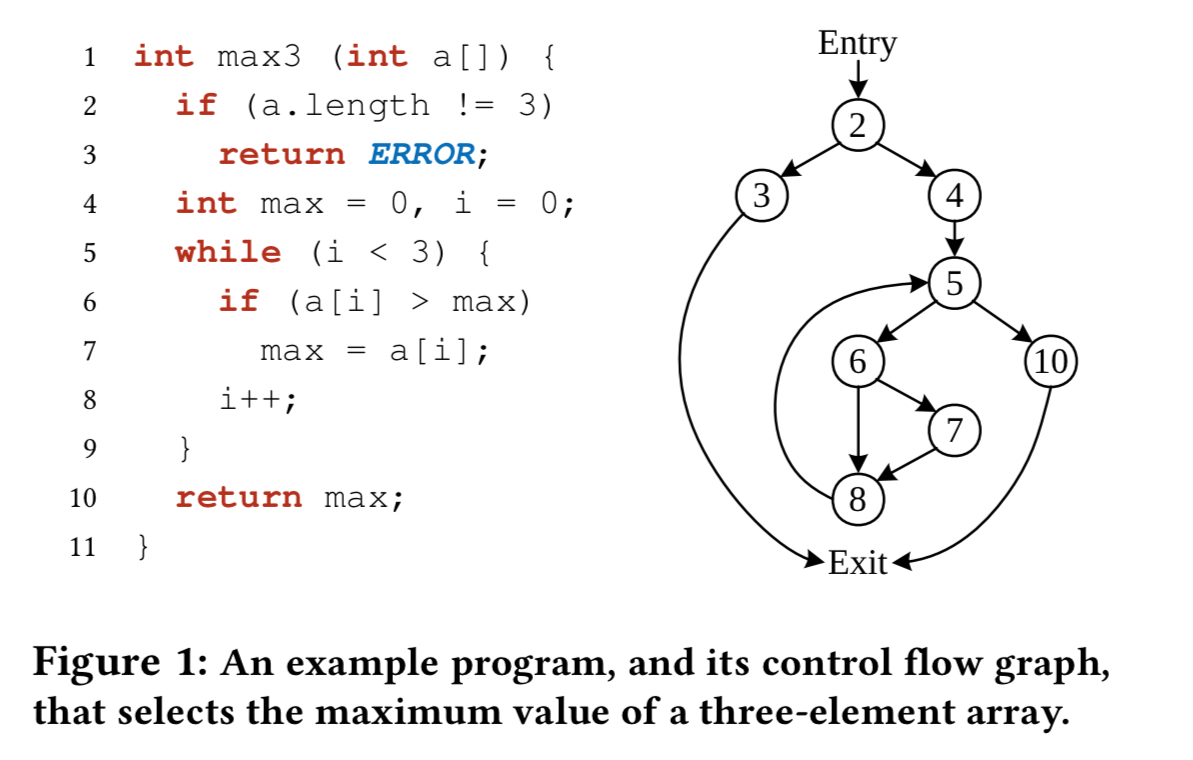
Here are some possible execution paths for the program, where blocks are identified by the line number on which they start:

Log20 samples the production system to collect path profiles. Let $p(x)$ be the number of occurrences of path $x$ divided by the total number of paths sampled in the system. In other words, $p(x)$ is an estimate of the probability of observing execution path $x$ . Using Shannon’s entropy we can measure the overall unpredictability in the system as:
$\displaystyle H(X) = - \sum_{x \in X} p(x) \log_2 p(x)$

We instrument a subset of the blocks. When execution follows a given path, it produces a log sequence containing log entries for the instrumented blocks only. Given a log sequence and a placement of log statements, it’s possible therefore that multiple execution paths may give rise to the same log sequence. As a trivial example, suppose that in our placement we have just one LPS in the block on line 2 – then any of the paths $P_1$ through $P_9$ will result in the same log sequence.

Let the Possible Paths of a log sequence $L_i$ , $PP(L_i) = {P_i, ..., P_j}$ be the set of paths that would output $L_i$ when executed.

Given a placement of log statements $S$ , then we can use entropy to model how much information we are getting from those log statements. Consider a particular log output $L$ , the entropy $H_L$ is:
$\displaystyle H_{L}(X) = - \sum_{x \in PP(L)} \frac{p(x)}{p(L)} \log_2 \frac{p(x)}{p(L)}$

Where $p(L)$ is the probability of the program taking a path that outputs L. $\frac{p(x)}{p(L)}$ is therefore telling us the probability that we took path $x$ given that we saw $L$ , $P(x | L)$ .

Now consider all possible log outputs produced by the placement $S$ . We can measure the entropy of the placement, $H_S$ as $H_{S}(X) = \sum_{L \in O(S)} p(L)H_L$ , where $O(S)$ is the set of all possible log sequences under placement $S$ . This reduces to:
$\displaystyle H_{S}(X) = - \sum_{x \in X} p(x) \log_2 \frac{p(x)}{p(L_x)}$

What’s the overhead of a log statement?

If we assume a fixed cost each time we emit a log statement, then the cost of given log statement placement is directly proportional to the number of times we expect it to be executed. We can figure this out from the production sampling, and assign each placement a weight $w$ representing that cost.

The Log20 placement algorithm

Given a set of basic blocks, BB, where each block has a weight, $w$ , the problem of placement is to find a subset of BB, $S \subset BB$ , such that the sum of the weights of all basic blocks in $S$ is under a threshold, $W_T$ , and entropy $H_S$ is minimized.

A brute force search is O(2^N), where N is the number of basic blocks, so that’s not going to work! Instead Log20 uses a greedy approximation algorithm. Sort the basic blocks in ascending order of weight (i.e., cheapest to instrument first). Considering them in this order, add them to the current placement if and only if adding the block under consideration both reduces the entropy and causes us to remain under the weight threshold.

One nice consequence of this is that all of the very rarely executed (and hence likely to be buggy) code paths tend to get instrumented.

Considering the example program we looked at earlier, with a weight threshold of 1.00 (on average there should be no more than 1.00 log entries printed by an execution path), then a single LPS should be placed at line 3 giving entropy 2.67. With a budget of 2.00, logging should be placed at lines 3 and 7.

Section 4.3 in the paper details an extension to the scheme I have just described which considers also logging variable values in LPSes. When these disambiguate later execution paths, logging such a value can reduce the number of downstream log statements required.

Implementation details

Log20 comprises an instrumentation library, a tracing library used for both request tracing and logging, and an LPS placement generator using the algorithm we just examined. The instrumentation library uses Soot for bytecode instrumentation.

The tracing library has low overhead and consists of a scheduler and multiple logging containers (one per thread), each with a 4MB memory buffer. Log entries are of the form timestamp MethodID#BBID, threadID plus any variable values. In the evaluation, each logging invocation takes 43ns on average, compared to 1.5 microseconds for Log4j.

If you’re feeling brave, you can even have Log20 dynamically adjust the placement of log statements at runtime based on continued sampling of traces.

Evaluation

The following charts show the relationship between overhead and entropy when using Log20 with HDFS, HBase, Hadoop YARN, and ZooKeeper. You can also see where the current manual instrumentation sits.

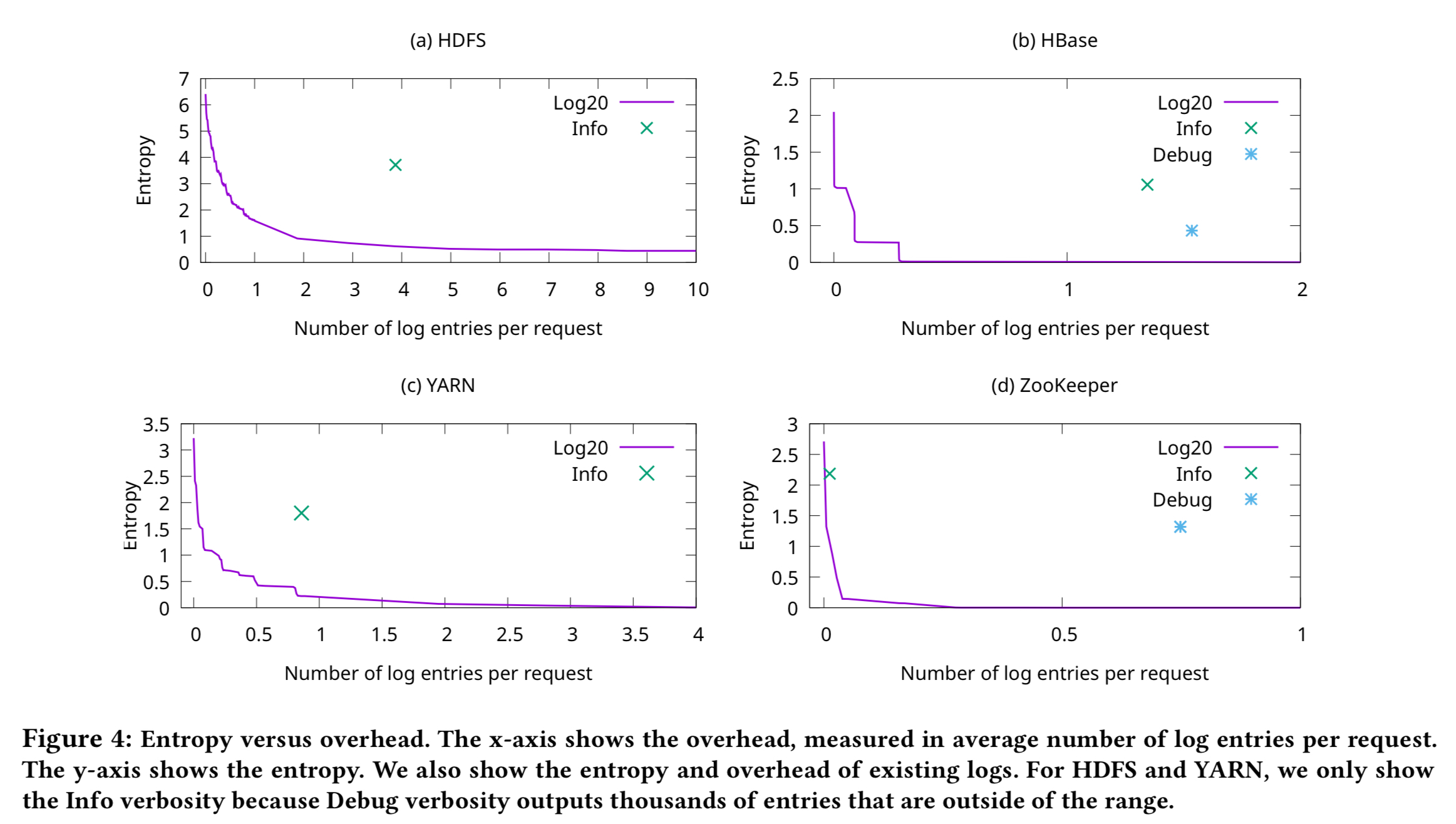
In HDFS, Log20’s placement can reduce the entropy from 6.41 to 0.91 with fewer than two log entries per request. Intuitively, this means that with two log entries per request, Log20 can reduce the number of possible paths from 2^6.41 (85) to 2^0.91 (2)… Log20 is substantially more efficient in disambiguating code paths compared to the existing placements.

For the same information level as existing Info logs, Log20 needs only 0.08 entries per request, versus 1.58 in the current system. If we consider Debug, Log20 needs just 0.32 log entries per request to achieve the same entropy as HDFS current 2434.92 log entries per request!

The real-world usefulness of Log20 for debugging was evaluated by looking at 41 randomly selected user-reported HDFS failures. Log20 was configured to hit the same performance threshold as the existing logs. Log20’s output is helpful in debugging 28 out of the 41. The existing log instrumentation helps in debugging 27.

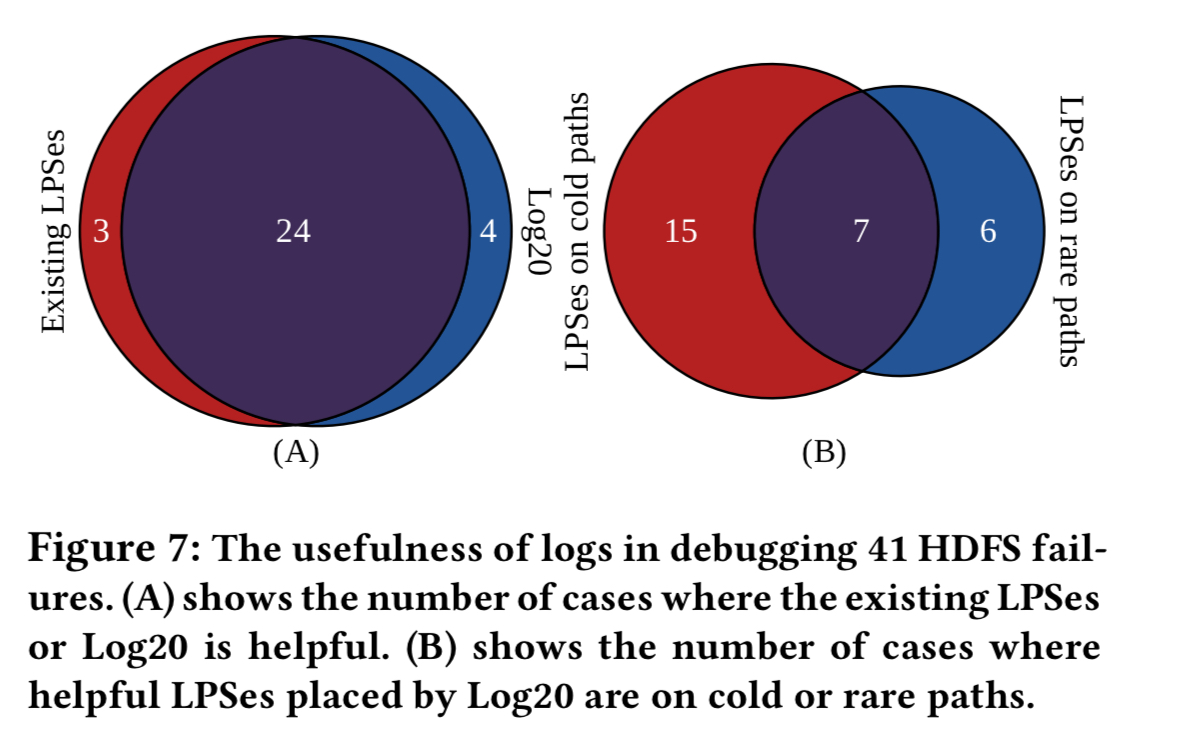
After all that work, it’s a little disappointing that for the same performance cost, Log20 doesn’t do much better overall. However, when we zoom into cold or rarely executed paths (see B) above, Log20 does indeed give much better coverage.

Guided by information theory, [Log20] measures how effective each logging statement is in disambiguating code paths. We have shown that the placement strategy inferred by Log20 is significantly more efficient in path disambiguation than the placement of log printing statements in existing programs.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic