Why does the neocortex have columns, a theory of learning the structure of the world Hawkins et al., bioRxiv preprint, 2017
Yesterday we looked at the ability of the HTM sequence memory model to learn sequences over time, with a model that resembles what happens in a single layer of the neocortex. But the neocortex has six layers. Today’s paper builds on the previous work to show how pairs of layers can learn predictive models of static objects, when the sensory input changes due to our own movement. For example, when our fingers touch an object.
Our research has focused on how the brain makes predictions of sensory inputs. Starting with the premise that all sensory regions make predictions of their constantly changing input, we deduced that each small area in a sensory region must have access to a location signal that represents where on an object the column is sensing. Building on this idea, we deduced the probable function of several cellular layers and are beginning to understand what cortical columns in their entirety might be doing.
Anatomical evidence
A few general rules have been observed for cellular layers in the neocortex:
- Cells in layers that receive direct feedforward input don’t send their axons outside the local region, and don’t form long distance horizontal connections within their own layer.
- Cells in layers driven by input layers do form long range connections within their layer, and also send an axonal branch outside of the region, representing an output.
The two layer input-output circuit thus formed appears between layer 4 and layer 2/3 of the six layers in the neocortex. Layers 6 and 5 may be a second instance of the pattern.
The prevalence of this two-layer connection motif suggests it plays an essential role in cortical processing.
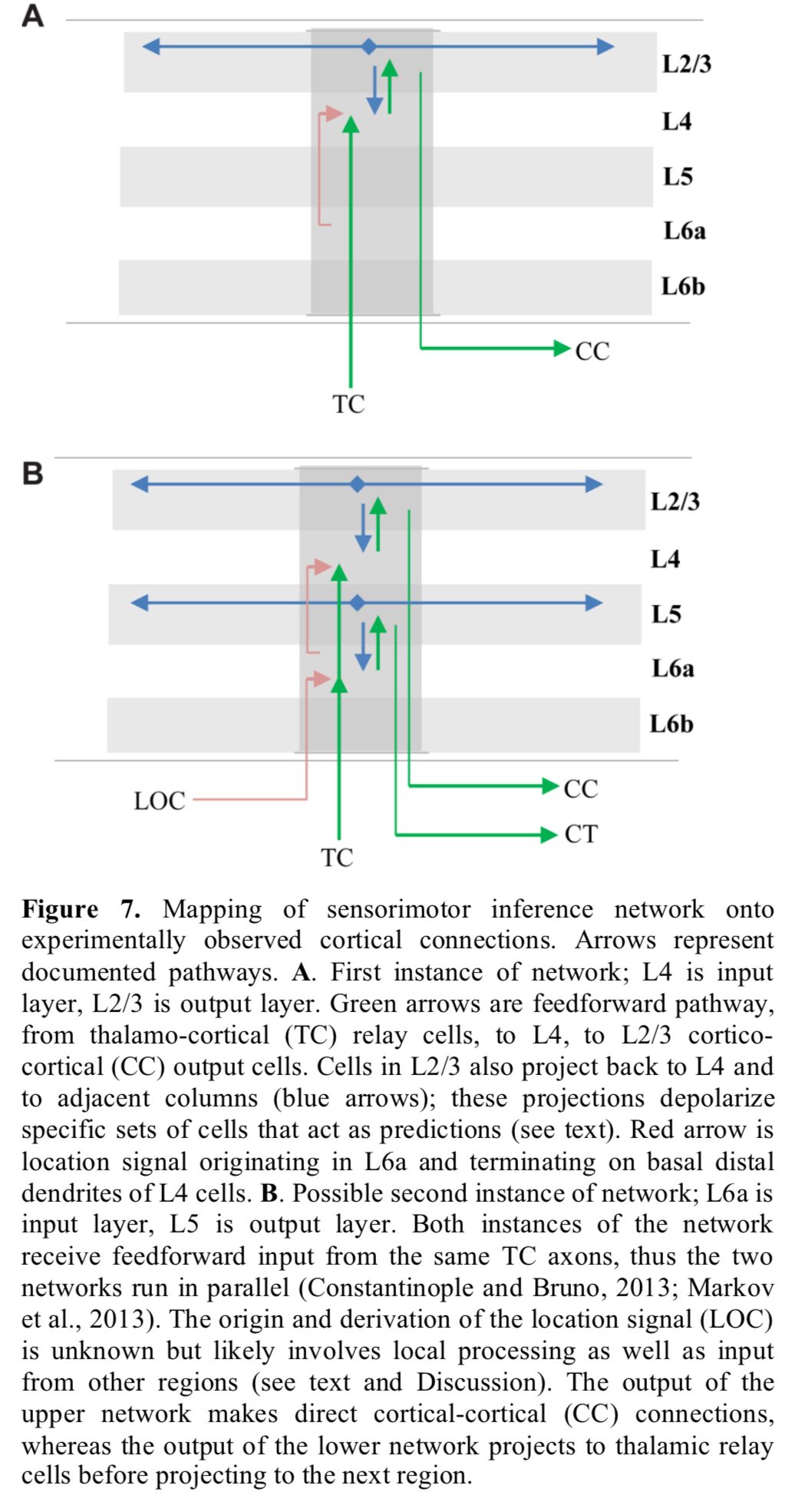
A key component of our theory is the presence in each column of a signal representing location. The location signal represents an “allocentric” location, meaning it is a location relative to the object being sensed.
The neurons effectively have to compute a predicted new location from the combination of current location, object orientation, and movement. That sounds a tall order, but we already know that grid cells in the entorhinal cortex perform these types of transformations, encoding the location of an animal’s body relative to an external environment.
These analogs, plus the fact that grid cells are phylogenetically older than the neocortex, lead us to hypothesize that the cellular mechanism used by grid cells were preserved and replicated in the sub-granular layers of each cortical column.
Enough of the biology, let’s now turn to the model it inspired.
Multi-layer model
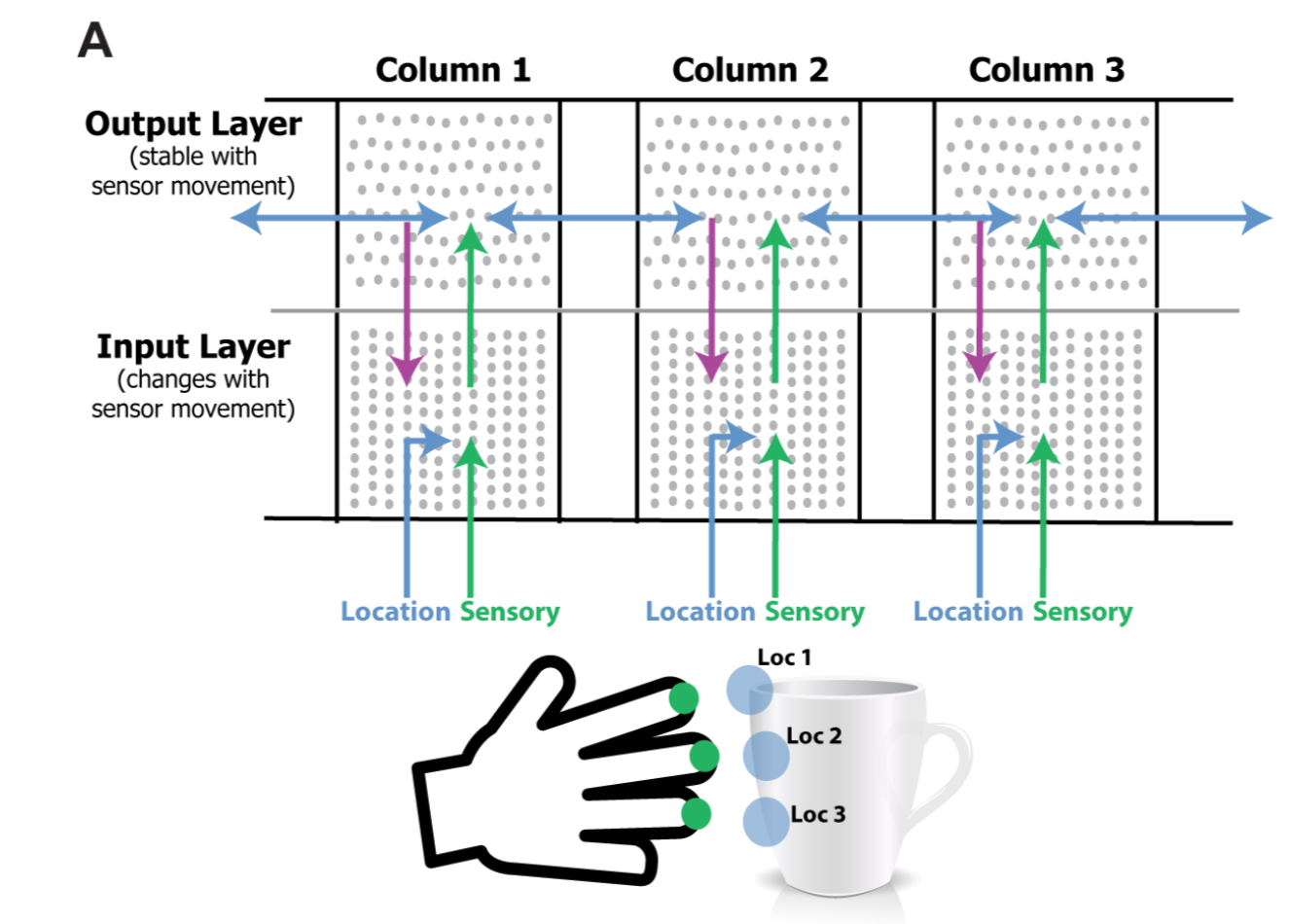
The current model consists of two layers of pyramidal neurons arranged in a column. The model has one or more of these columns. Each cortical column processes a subset of the sensory input space and is exposed to different parts of the world as the sensors move.
The neurons used in the model are HTM model neurons as we looked at yesterday.
Input layer
The input layer of each column consists of HTM neurons arranged in mini-columns. It receives a sensory input as a feedforward input, and a location input as a basal modulatory input. The sensory input is a sparse binary array representing the current feature in input space.
During inference, cells that recognize both the modulatory location input and the feedforward driving input will inhibit other cells in the mini-column.
In this way, the input layer forms a sparse representation that is unique for a specific sensory feature at a specific location on the object.
Neurons in the input layer also receive feedback connections from the output layer. These carry information about the object detected, which combined with modularity input representing the anticipated new location, allow the input layer to more precisely predict the next sensory input.
Output layer
The output layer is also made up of HTM neurons. The set of cells that are active in the output layer represent objects. Output layer cells receive feedforward input from the input layer, and modulatory input from other output cells representing the same object, both within the column and also from neighbouring columns.
During learning, the set of cells representing an object remains active over multiple movements and learns to recognize successive patterns in the input layer. Thus, an object comprises a representation in the output layer, plus an associated set of feature/location representations in the input layer.
Cells representing the same object positively bias each other. Say at time t, a column has feedforward support for objects A and B. And at time t+1 it has feedforward support for objects B and C. Due to the modulatory input from time t, the output layer will converge on the representation for B.
Example: cubes and wedges
The following figure shows two layers of a single cortical column collaborating to disambiguate between a cube and a wedge shape that have shared features. The first sensed feature f1 is ambiguous so the output layer supports both object patterns, but with repeated sensations the output layer quickly narrows down on the correct choice (the cube in this case).
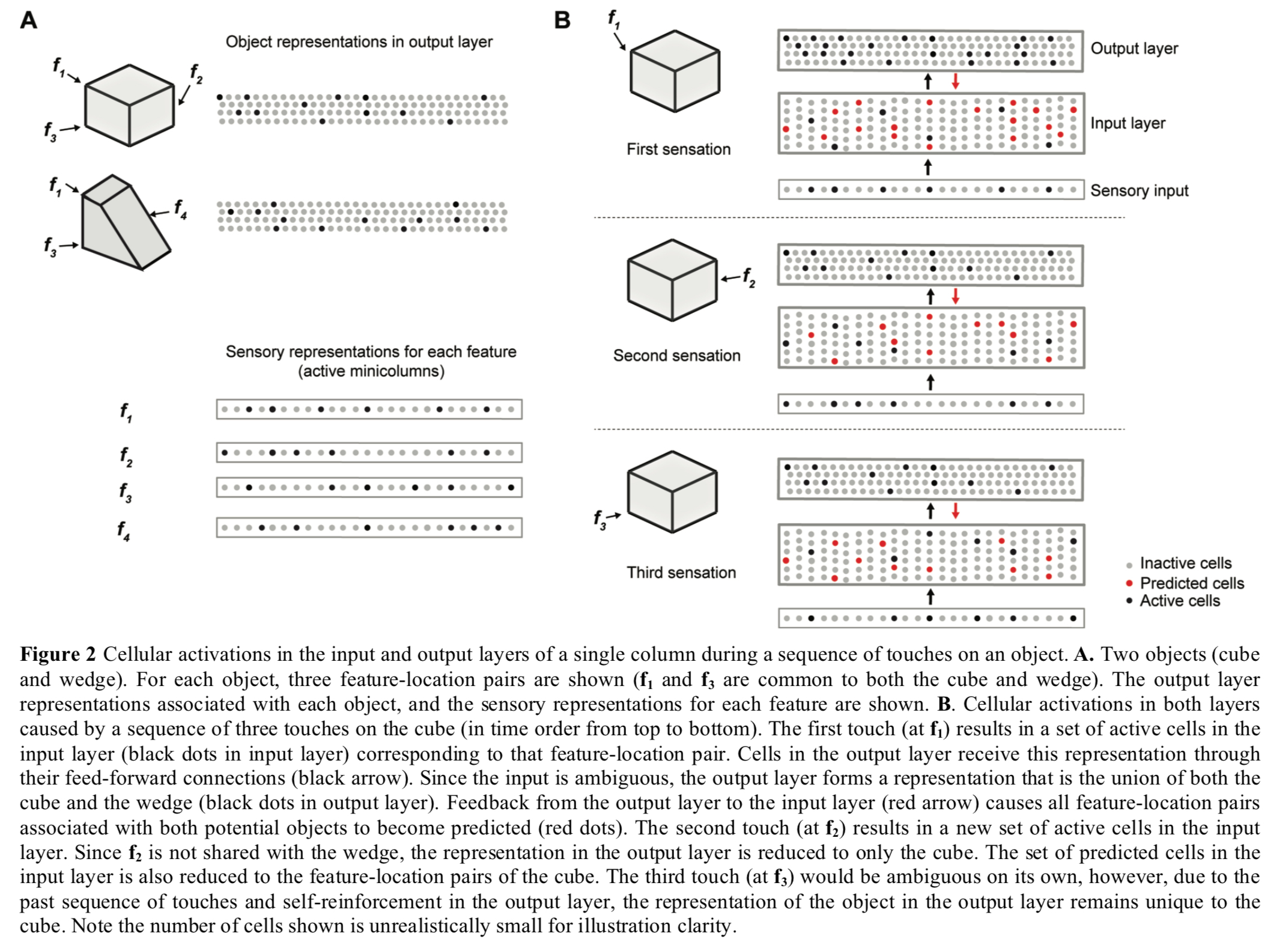
(Enlarge)
Learning
Learning is based on Hebbian-style adaptation as we saw yesterday. The input layer learns specific feature/location combinations, and if the current combination has not yet been learned, then one cell from each mini-column (the one with the best modulatory input match) is chosen as the winner and becomes active. Winner cells learn by forming and strengthening modulatory connections with the current input location.
The output layer learns representations that correspond to objects:
When the network first encounters a new object, a sparse set of cells in the output layer is chosen to represent the new object. These cells remain active while the system senses the object at different locations. Feed forward connections between the changing active cells in the input layer and unchanging active cells in the output layer are continuously reinforced.
Simulation results
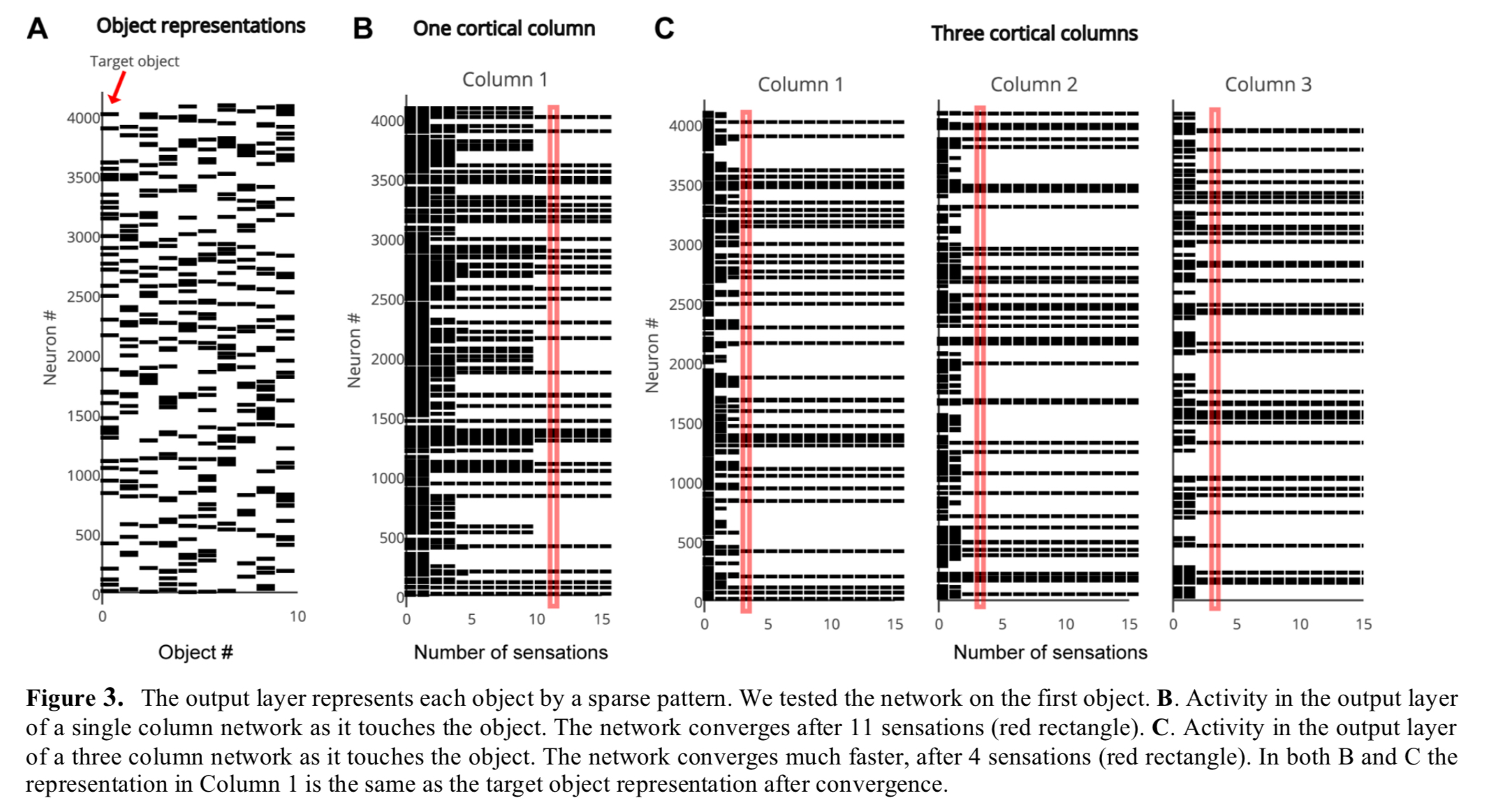
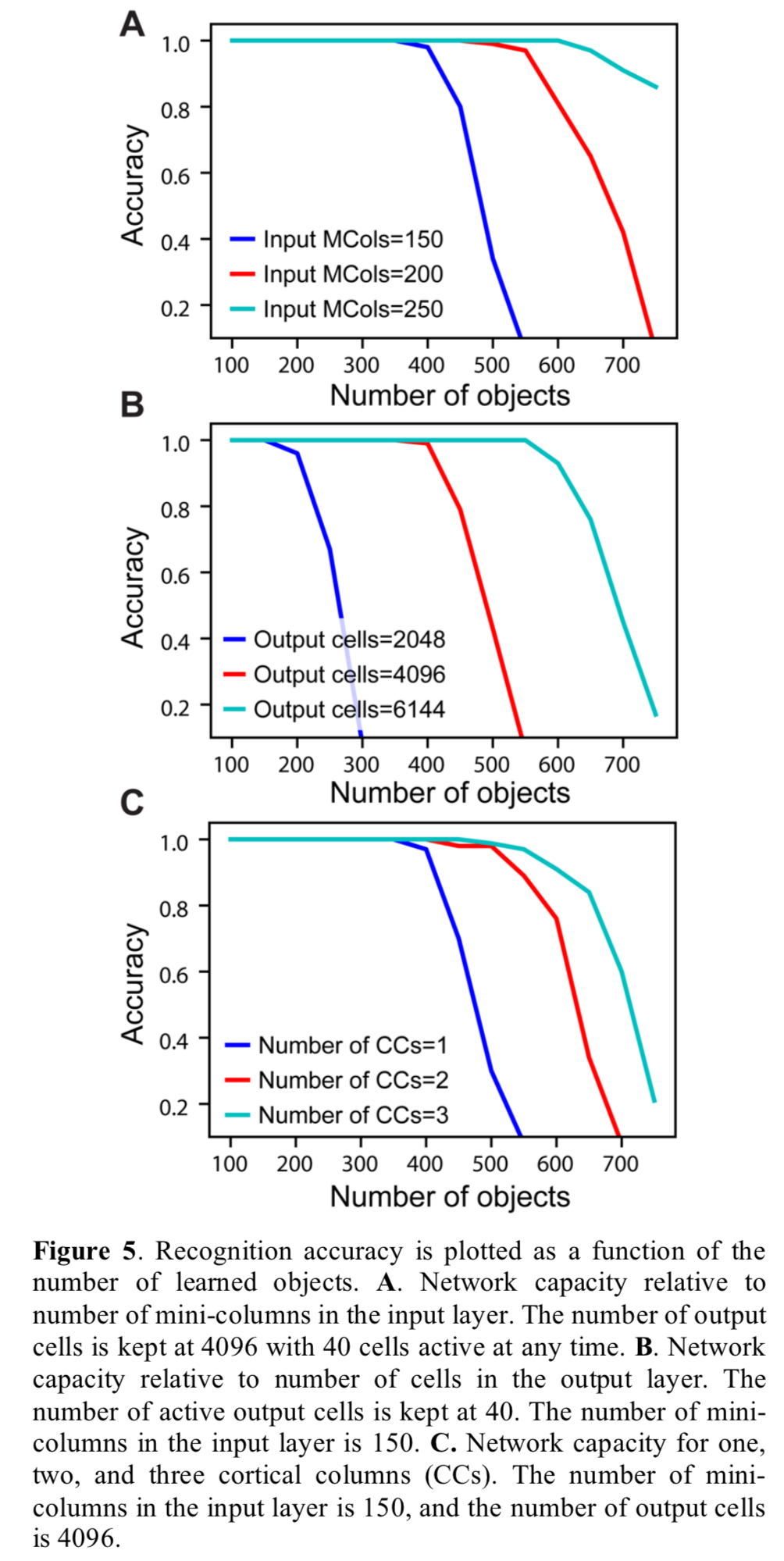
Networks are constructed with one or more two-layer cortical columns. In each column the input layer comprises 150 mini-columns, 16 cells tall each. The output layer consists of 4096 cells, which are not arranged in mini-columns. One-column and three-column variations of the network are trained on a library of 500 objects. As can be seen below, both variations converge on a single object representation over time, but the three-column version gets there faster.
The capacity of the network is defined as the number of objects it can learn and recognise without confusion. It is influenced by the representational space of the network, the number of mini-columns in the input layer, the number of neurons in the output layer, and the number of cortical columns. 150 mini-columns with 16 cells per mini-column, and 10 simultaneously active mini-columns, turns out to be enough to uniquely represent about 10^15 sensory features, each represented at 16^10 unique locations.
As the number of learned objects increases, neurons in the output layer form increasing numbers of connections to neurons in the input layer. If an output neuron connects to too many input neurons, it may be falsely activated by a pattern it was not trained on. Therefore, the capacity of the network is limited by the pooling capacity of the output layer. Mathematical analysis suggests that a single cortical column can store hundreds of objects before reaching this limit.
Figure 5 below explores the various dimensions of network capacity.
The network shows no drop in recognition accuracy with up to 20% noise in the sensory input, and 40% noise in the location input, though it does take longer to converge.
Mountcastle’s conjecture
In 1978 Mountcastle postulated that since the complex anatomy of cortical columns is similar in all of the neocortex, then all areas of the neocortex must be performing a similar function…
The model of a cortical column presented in this paper is described in terms of sensory regions and sensory processing, but the circuitry underlying our model exists in all cortical regions. Thus if Mountcastle’s conjecture is correct, even high-level cognitive functions, such as mathematics, language, and science would be implemented in this framework. It suggests that event abstract knowledge is stored in relation to some form of “location” and that much of what we consider to be “thought” is implemented by inference and behavior generating mechanisms originally evolved to move and infer with fingers and eyes.