An efficient bandit algorithm for realtime multivariate optimization Hill et al., KDD’17

Aka, “How Amazon improved conversion by 21% in a single week!”

Yesterday we saw the hard-won wisdom on display in ‘seven myths‘ recommending that experiments be kept simple and only test one thing at a time, otherwise interpreting the results can get really complicated. But sometimes the number of combinations you might need to test can grow really big really fast. Consider the problem of trying to find a near-optimal version of a promotional message such as this one, which has 5 variable parts and 48 different combinations in total.

Based on the Amazon success rate and traffic size, the authors calculated it would take 66 days to conduct a 48 treatment randomized experiment. Often this isn’t practical.

Even a small set of decisions can quickly lead to 1,000’s of unique page layouts. Controlled A/B tests are well suited to simple binary decisions, but they do not scale well to hundreds or thousands of treatments.

Amazon adapted a multi-armed bandit approach with Thompson sampling (balancing exploration and exploitation) to work in a realtime multivariate optimization setting. Or in plain English, they test lots of different things all at once and use a controlled search through the space to converge on a near-optimum.

We name our approach multivariate bandits to distinguish from combinatorial bandits which are used to optimize subset selection.

The approach was deployed in a live production setting at Amazon, to optimise the promotions box we saw above. Within just one week it found a combination that increased purchased by 21% compared to the median performing layout. In a world of intense competition where faster feedback wins, that’s a noteworthy result.

We are actively deploying this algorithm to other areas of Amazon.com to solve increasingly complex decision problems.

If you want to move at the speed of Amazon, here’s how it works…

An abstract model of the problem

We want to select a layout A of a web page under a context X in order to maximise the expected value of a reward R. Here R is the value of an action taken by a user after viewing the web page. In the simplest case R is binary, the user either takes the desired action or they don’t (the technique can be extended to numerical or categorical outcomes). Unlike in A/B testing where we typically try to control all other variables, here the context X explicitly models user or session information that may impact a layout’s expected reward: things like time of day, device type, user history and so on.

To keep things simple again, let’s say that the layout A has D components or widgets, each of which has N alternative variations (accommodating differing numbers of variations for the different widgets is entirely possible, as was done in the production experiment).

We can represent a layout A as a D-dimensional vector, where denotes the content chosen for the widget. X and_A_ can be combined (possibly non-linearly) to form a feature vector .

The reward for a given layout and context depends on some linear scaling of by a fixed but unknown vector of weights .

This all sounds quite fancy. But all we’ve really got going on here is a system of the form:

Where etc, are constants (weights) in the vector , are the context variables, and are the layout variables.

We now define a stochastic contextual multi-armed bandit problem. We have N^D arms, one per layout.

At each time step , we select an arm and observe the reward . We always have a best-so-far arm, and the overall aim is to estimate the coefficients while minimising the regret we feel from sometimes choosing an arm that isn’t as good as the best-so-far.

The contextual bandit with linear reward problem has been well studied…

Since we’re dealing with binary rewards, we can use the probit function in regression. To avoid combinatorial explosion (N^D) the model only captures pairwise interactions and ignores any higher order effects. It all ends up looking like this, but for our purposes it’s enough to get the general idea:

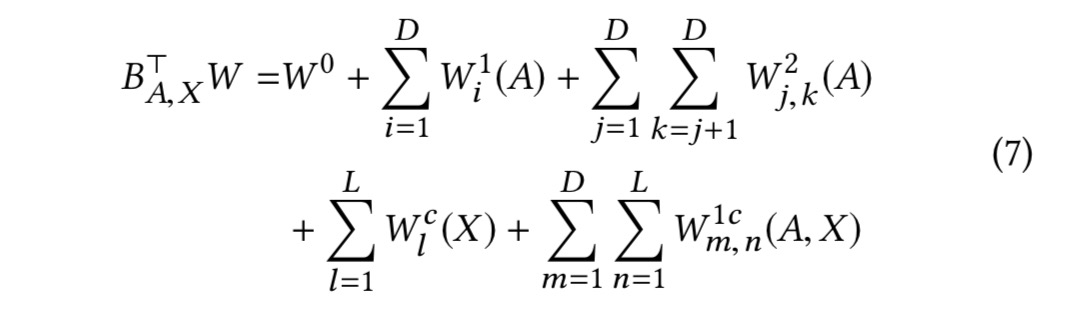
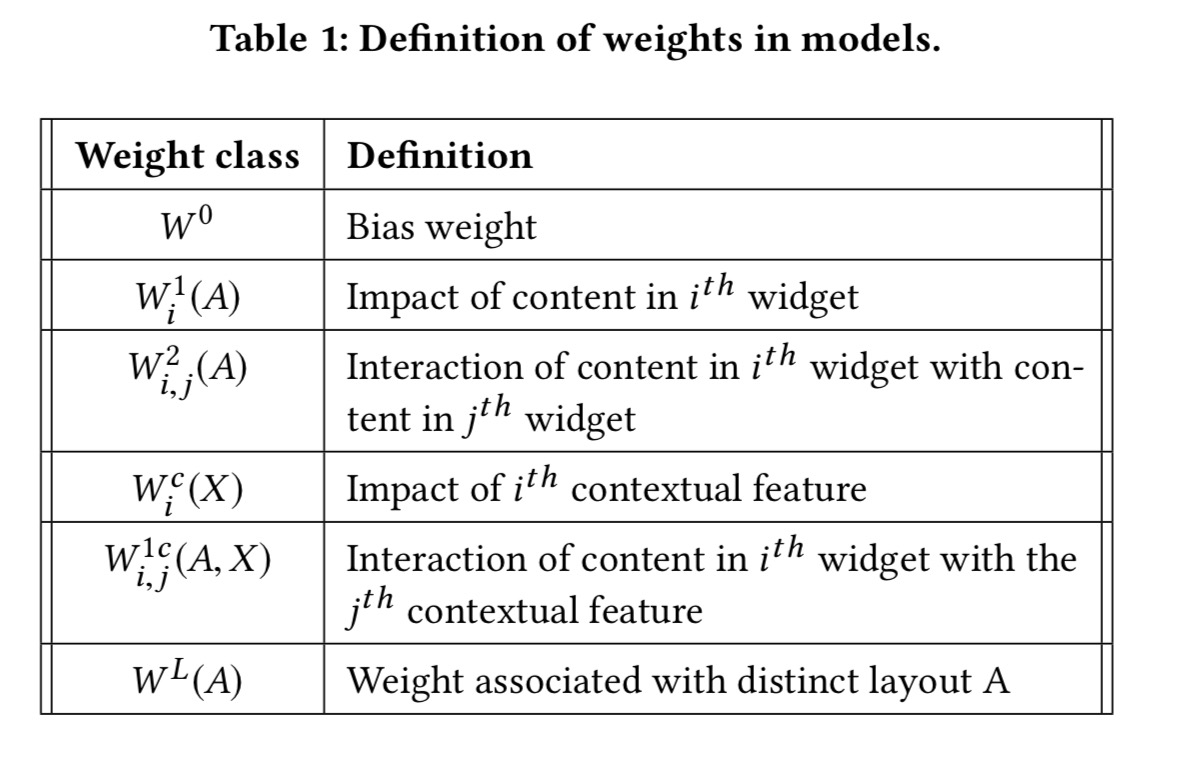
Thomson sampling is used to balance exploration (choosing an arm that isn’t the best so far) and exploitation of the best so far.

Thomson sampling selects a layout proportionally to the probability of that layout being optimal conditioned on previous observations… In practice this probability is not sampled directly. Instead one samples model parameters from their posterior and picks the layout that maximizes the reward.

The only slight issue here is that line 4 is an NP-hard problem (the maximum edge-weighted clique problem). But all is not lost! We can approximate it with a greedy hill climbing algorithm.

We perform hill climbing S times where each iteration s uses a different initial random. We return the best layout among the S hill climbs…

Results from production

Section 4 in the paper contains a whole set of simulation results that I’m going to skip right over, because the bottom line is always how well it works in production. The version actually used for the production test (MVT2) didn’t include any context vector though.

We applied MVT2 to optimize the layout of a message promoting the purchase of an Amazon service. The message was shown to a random subset of customers during a visit to Amazon.com on desktop browsers. The message was constructed from 5 widgets: a title, an image, a list of bullet points, a thank-you button, and a no-thank-you hyperlink. Each widget could be assigned one of two alternative contents except for the image which had three alternatives. The message thus had 48 total variations.

As a baseline, MVT2 was also compared against a multi-armed bandit model with 48 arms (but no interactions between widgets) – dubbed N^D-MAB – and a model using one multi-armed bandit per widget, testing each of the options just for that one widget (D-MAB).

The experiment ran for 12 days, with tens of thousands of impressions per algorithm per day. Layouts were selected in real-time using Thomson sampling, and the model was updated once a day using the previous day’s data.

Here are the results for the three algorithms, where convergence is the proportion of trials on which the algorithm played its favourite layout. By the time you reach a convergence value of 1, the algorithm is always making the same (hopefully optimal!) choice.

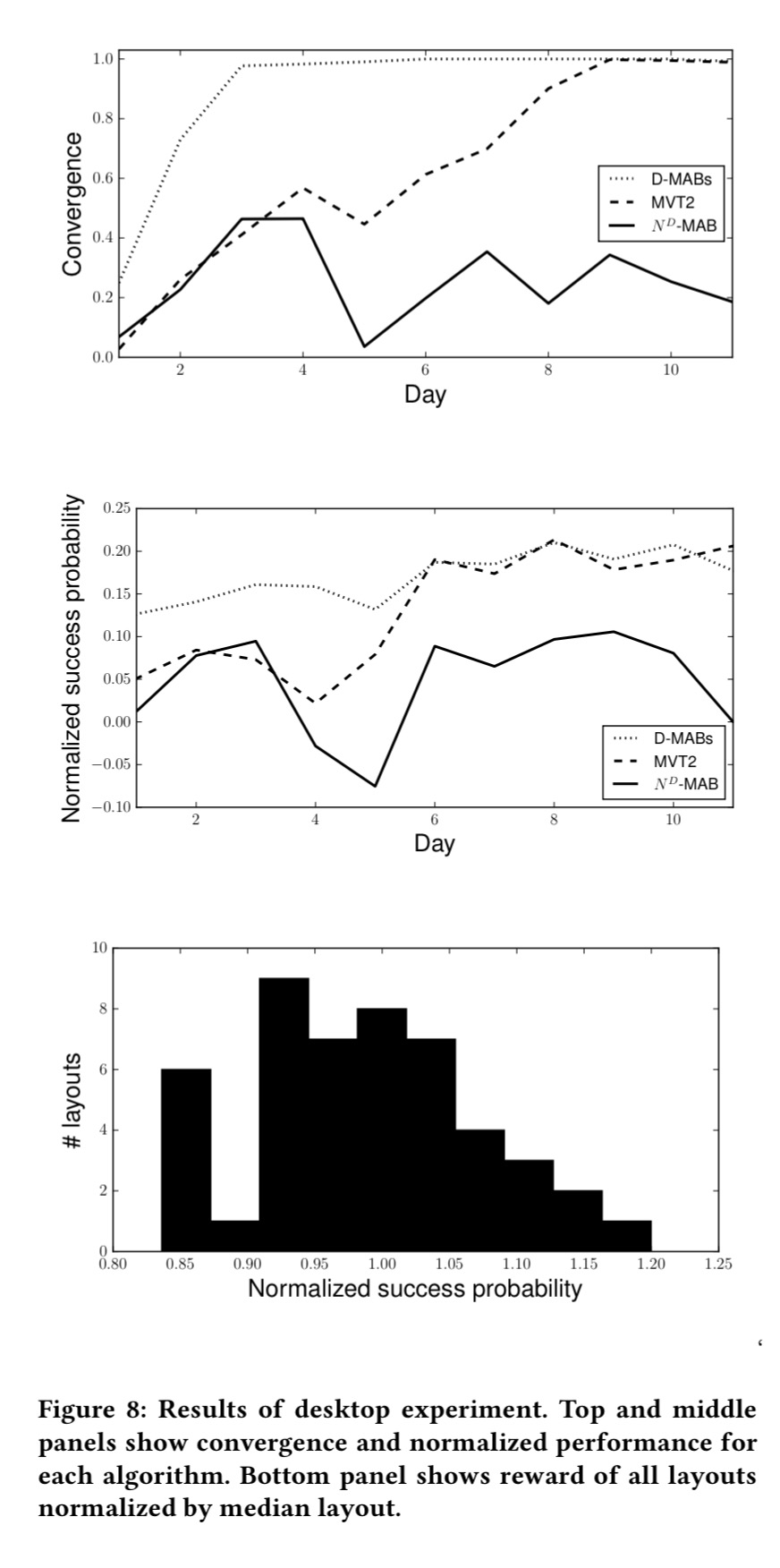
The normalised success probability chart tells you the percentage increase (e.g., 0.2 = 20%) over the performance of the median layout.

… the winning layout for this experiment showed a 21% lift over the median layout and a 44% lift over the worst performing layout. If different content had a negligible impact on customer behaviour, no algorithmic approach would provide much benefit in optimization. However, given these surprisingly large lifts, there appears to be a large business opportunity in combinatorial optimization of web page layouts.

The uplift is clearly something Amazon are very happy with, but it’s a little disappointing that after all that effort building a model where including contextual inputs and capturing widget interactions are both major features, the former wasn’t used at all and the latter didn’t seem to make much difference. (The D-independent multi-armed bandit baseline did just as well if not better). However:

While we did not find significant 2nd or 3rd order interactions in this experiment, this observation does not generalize. In a follow-up experiment, we applied MVT2 to the mobile version of the promotional page. The template… has a total of 32 possible layouts. In this case, we found that 2nd order (p \ … our algorithm can be applied to any problem that involves combinatorial decision making. It allows for experimental throughput and continuous learning that is out of reach for traditional randomized experiments. Furthermore, by using a parametric modeling approach, we allow business insights to be extracted directly from the parameters of the trained model.

A recent article on the ConversionXL website has a nice succinct discussion of the differences between A/B, multivariate, and bandit algorithms and advice on when to use each of them.

The authors finish with a very interesting point – because the multi-variate approach allows faster testing of lots of different ideas and it can rapidly filter out bad choices, it encourages exploring a few riskier and more creative options. Most of these may turn out to be bad, but I suspect the winners are more likely to have outsized returns.