Enabling signal processing over data streams Nikolic et al., SIGMOD ’17
If you’re processing data coming from networks of sensors and devices, then it’s not uncommon to use a mix of relational and signal processing operations.
Data analysts use relational operators, for example, to group signals by different data sources or join signals with historical and reference data. They also use domain-specific algorithms such as Fast Fourier Transform (FFT) to do spectral analysis, interpolation to handle missing values, or digital filters to recover noisy signals.
This can be accomplished in environments such as SQL Server, Greenplum and Spark through integration with R. The trouble is that there’s an impedance mismatch between the world of relational query processing and the world of R / signal processing. General purpose streaming engines support relational and streaming queries over relational or tempo-relational data, whereas numerical tools typical support offline operations on arrays. This leads to a lot of inefficiency every time you cross between the two worlds. For real-time processing of streaming data, the overheads can easily be unacceptable.
TrillDSP, which builds on top of the Trill streaming analytics engine from Microsoft, provides a deep integration of digital signal processing (DSP) operations and the Trill general purpose query processor. It provides a nice example of the benefits and elegance of doing so, so let us hope we see similar developments for other stream processing engines following suit.
We have built a query engine, named TRILLDSP, that deeply integrates relational and signal processing… (1) it provides a unified query language for processing tempo-relational and signal data; (2) its performance is comparable to numerical tools like MATLAB and R and orders of magnitude better than existing loosely-coupled systems; (3) it provides mechanisms for defining custom DSP operators and their integration with the query language; (4) it supports incremental computation in both offline and online analysis.
An example of mixed relational and signal processing
Consider an IoT application receiving a stream of temperature readings from different sensors in time order. We want to run a five-stage processing pipeline on the signal coming from each source:
- Grouping by source, while retaining time order inside each group
- Interpolation to provide a uniformly sampled signal suitable for feeding to a DSP algorithm
- Windowing to create 512-sample windows of data with a 256 sample hop size
- Spectral analysis of each window using FFT: a frequency representation is computed at each hopping point, and then a user-defined function (e.g., retaining only the top-k spectrum values) operates on the frequency representation. Finally, an inverse FFT operation is performed to transform the samples back again.
- Unwindowing, to restore the original signal form – projecting output arrays back to the time axis and summing up the overlapping values.
Here’s how we can express the computation in TrillDSP:

And for comparison, this is what it would look like in native R:
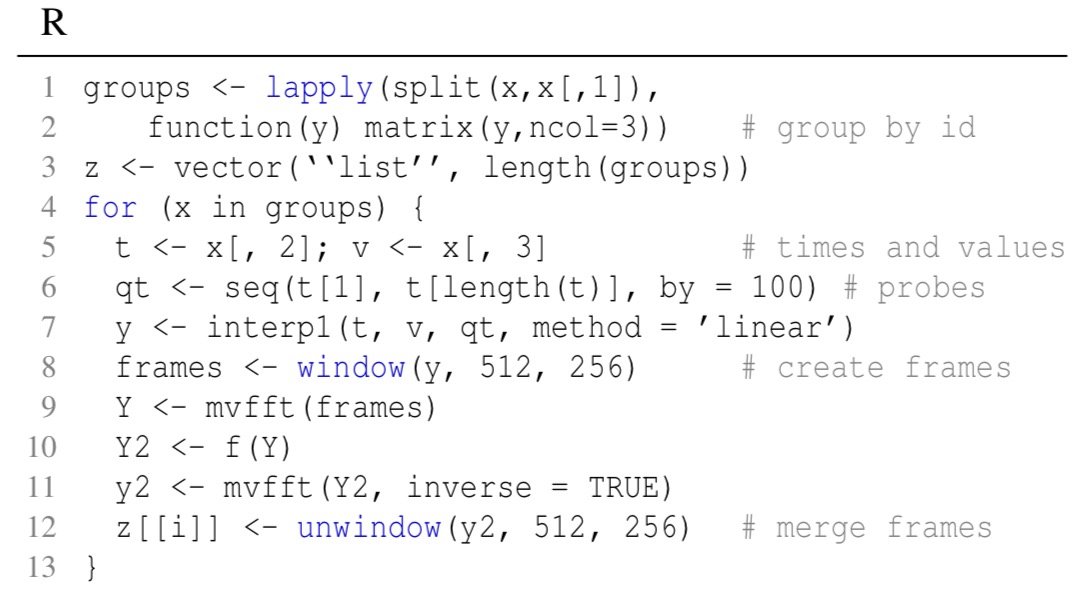
And in SparkR:

For pure DSP tasks, TrillDSP is comparable with or better than best-of-breed signal processing systems such as MATLAB, Octave, and R. It also outperforms WaveScope, another streaming engine with DSP support.
For queries mixing relational and signal processing, TrillDSP shows up to 146x better performance than loosely-coupled systems such as SparkR and SciDB-R.
TrillDSP: From streams to signals
We know that we need data in array format for DSP operations, but TrillDSP chose not to make arrays first-class citizens in the data model. Instead, arrays are exposed only through designated DSP operators that hide the complexity of on-the-fly translation between relational and array models. This preserves the performance and query language for the existing relational API, while still giving DSP experts what they need. An initial loose coupling design (shelling out to R) spent more than 91% of the total execution time just in translation between relational and array formats. Supporting DSP operations in-situ is required for good performance:
IoT applications run the same query logic over many sensor devices. For that reason, we design signal operations to natively support grouped processing and implement them as stateful operators that internally maintain the state of each group. Coupling these operators with Trill’s streaming temporal MapReduce operator is key to efficient grouped signal processing, as seen in experiments.
Signals are treated as a special kind of stream in which stream events have no overlapping lifetimes. If a stream does has events which overlap in time, on simple way to convert the stream to a signal is to average overlapping stream events on the value field. In TrillDSP:
var s0 = steam.Average(e => e.Value)
We’ll see how to create uniformly sampled signals in the next section.
Signal payloads can be of arbitrary structure, including complex and real-valued signals, so long as the payload type implements the following interface:

Thus customized signal payloads can be used for processing in different application domains. As well as discrete-time signals users may also want to work with more general continuous signals whose values can be expressed as a function of time.
For example, in amplitude modulation, users multiply a signal with a continuous carrier signal, which is usually a sine wave of a given frequency and amplitude… To capture continuous signals efficiently, TrillDSP introduces functional signal payloads that carry a lambda function for computing signal values at any point in time.
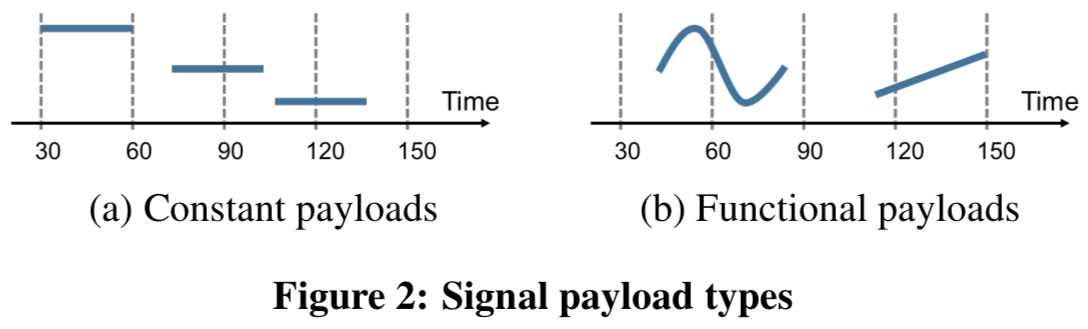
You can either specify a function per event, or the more efficient function per signal.
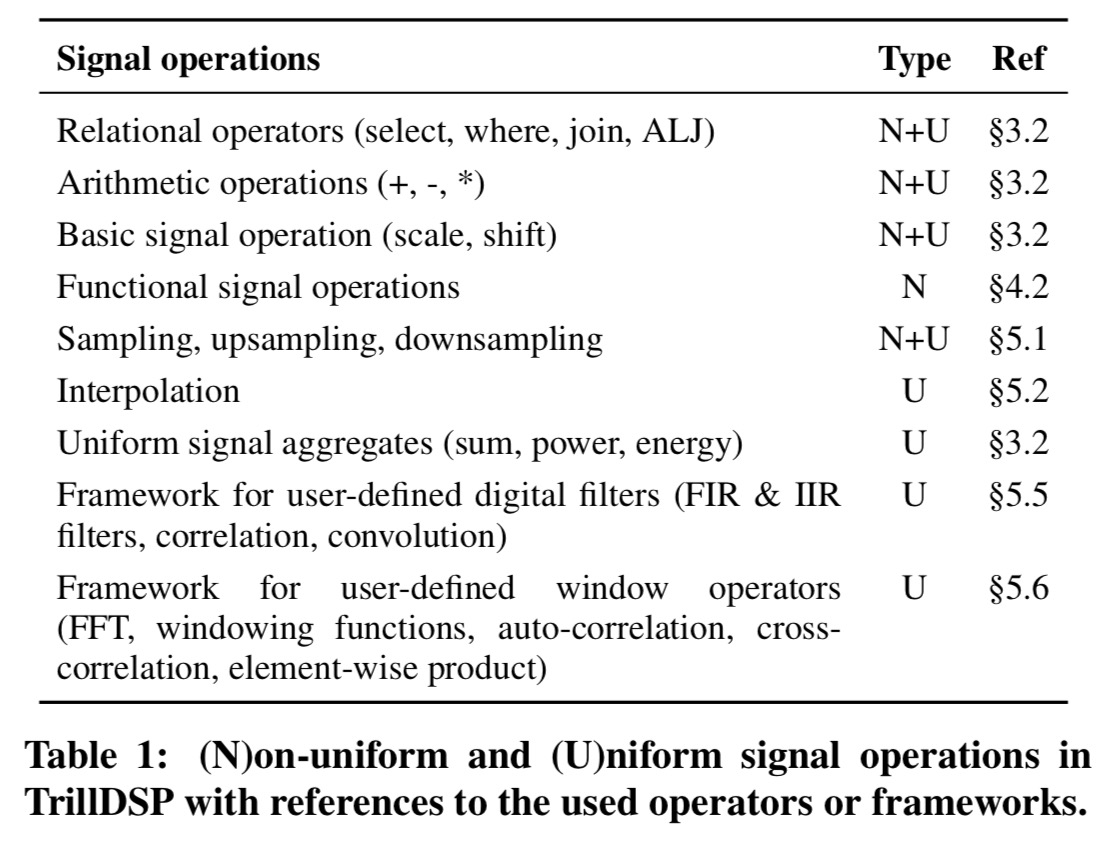
TrillDSP supports a wide range of operations on signals as shown in the following table:
Uniformly-sampled signals
Most DSP algorithms expect signals of equally spaced samples. Uniform signals in TrillDSP are defined by a sampling period and a sampling offset. The offset defines the initial time shift of samples and is useful for correlating. The TrillDSP Sample operator produces a uniform signal by sampling a non-uniform one. To handle irregular events, the Sample operator can be passed an interpolation policy, that specifies the rules for computing missing values. A policy consists of an interpolation function and an interpolation window size determining the maximum time distance among reference samples used for interpolation.
TrillDSP provides a set of common interpolation functions: constant, last-valued, step (zero-order), linear (first-order), and second-degree polynomial (second-order), and also supports user-defined interpolation functions.
Signal windows are implemented as fixed-size circular arrays to efficiently support offline and online processing with overlapping windows.
For binary operation on uniformly sampled signals the operands need to share the same sampling period and offset. TrillDSP provides resampling operations (upsample, downsample, and resample) that allow users to change these properties on the fly.
Digital filters
Custom digital filters can be written by specifying the sizes of the feed-forward and feeb-backward windows, how to interpret missing values, and the filtering function itself. Such filters implement the following interface:

As an example, a finite impulse response (FIR) filter produces outputs which are the weighted sums of the most recent inputs. It uses only the feed-forward loop, and can be implemented in TrillDSP as follows:

Windowing
We briefly saw the windowing support when we looked at an example pipeline earlier. The Window operator supports the fundamental windowing workflow when analyzing uniform signals.
The workflow consists of three steps: (1) the first step splits the signal into smaller, possibly overlapping components, (2) the second step transforms each component using a sequence of operations, and (3) the third step recombines the processed components into the final signal.
The transformations in step 2 are expressed as a pipeline of operators. Each pipeline operator implements an interface providing support for incremental computation and re-evaluation. For many signal operations, re-evaluation is the only option.
Evaluation
TrillDSP’s pure DSP performance is evaluated against MATLAB, Octave, and R. For workloads combining relational and signal processing (i.e., the target workloads), TrillDSP is evaluated against Spark with R integration, SciDB with R integration, and WaveScope (the system closest in spirit to TrillDSP).
Here’s a pure DSP example based on FIR filtering (note the log axis):
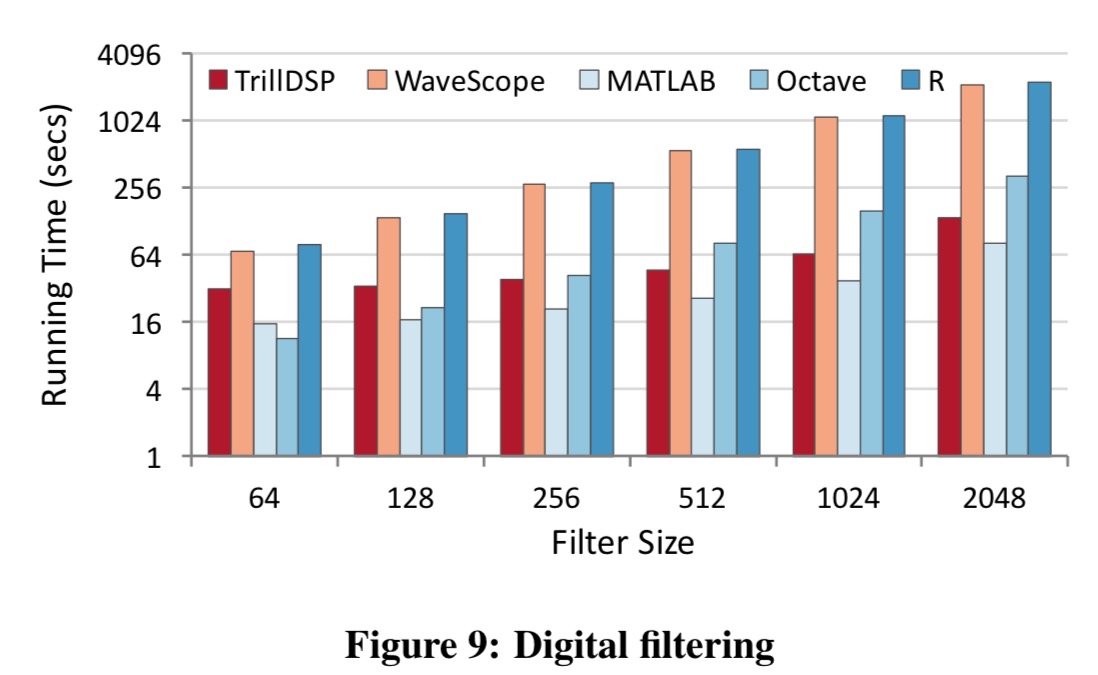
TrillDSP’s SIMD implementation of dot product outperforms the naïve loop implementation in WaveScope and R by a wide margin. TrillDSP stays competitive with Octave while being up to 1.8x slower than MATLAB. In contrast to the offline tools, TrillDSP incurs additional overheads from copying stream events into arrays and checking for missing values. These experiments demonstrate that TrillDSP can easily integrate with 3rd-party libraries to deliver performance competitive with or even better than the state-of-the-art tools used by practitioners in offline analysis.
Of course, beyond just performance, TrillDSP also offers true online support and tight integration with relational operators. Consider an example of grouped signal interpolation and filtering. The task is to take two uniformly sampled signals with different sampling periods, group them by sensor id, and in each group upsample the first signal to match the sampling period of the second before reporting events at which both group signals have simultaneously extreme values.
The following chart shows the running time of various systems normalized by the running time of TrillDSP with 16 cores over varying numbers of groups. (So for example, a value of 4 on the y-axis means that configuration is 4x slower than TrillDSP with 16 cores on the same task). Note again the log scale on the y-axis.
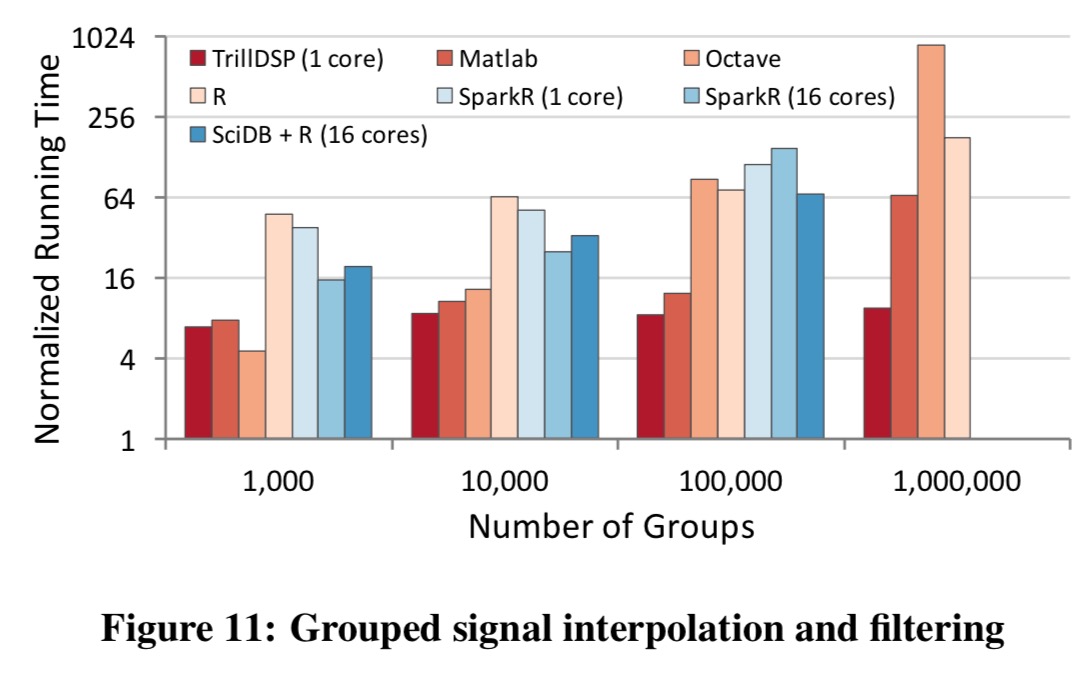
We note that even the single-threaded TRILLDSP program outperforms all the other systems in all but one cases due to its group-aware interpolation operator simultaneously processing multiple subsignals. Running TRILLDSP using 16 cores accelerates the single-threaded performance by up to 9.4 times, which leads to much better performance overall, up to 146x faster than SPARKR and up to 67x faster than SCIDB-R. Both of these systems behave poorly for large numbers of groups, eventually crashing when processing one million groups. Such bad performance was primarily caused by expensive reshuffling operations, which in SPARKR also involve writing to disk.