Semi-supervised knowledge transfer for deep learning from private training data Papernot et al., ICLR’17

How can you build deep learning models that are trained on sensitive data (e.g., concerning individuals), and be confident to deploy those models in the wild knowing that they won’t leak any information about the individuals in the training set? As ML/DL is increasingly integrated into every aspect of modern businesses, this becomes a really important question. ‘Semi-supervised knowledge transfer for deep learning from private data’ shows us a broadly applicable and easily understandable technique for doing just this, based on the gold standard of differential privacy. It won a best paper award at ICLR’17, and rightly so!

The trouble with training on sensitive data

Some machine learning applications with great benefits are enabled only through the analysis of sensitive data, such as users’ personal contacts, private photographs or correspondence, or even medical records or genetic sequences. Ideally, in those cases, the learning algorithms would protect the privacy of users’ training data, e.g., by guaranteeing that the output model generalizes away from the specifics of any individual user. Unfortunately, established machine learning algorithms make no such guarantee…

During model training, it’s difficult not to end up with some degree of overfitting, in which specific training examples can be implicitly memorised. It is possible to recover private/sensitive training data in this case. This has been shown to be possible even without access to the model’s parameters. “For example, Fredrikson et al., used hill climbing on the output probabilities of a computer-vision classifier to reveal individual faces from the training data.”

A private aggregation of teacher ensembles

The approach to privacy outlined in this paper is called PATE, for Private Aggregation of Teacher Ensembles. It provides differential privacy guarantees even in the worst case of a model’s architecture and parameters being leaked. The fundamental idea is that you can’t leak information you never knew in the first place. The authors set up such a situation using a level of indirection.

First the training data is partitioned into disjoint subsets, and n instances of a classifier are trained, one per subset. (In fact, you don’t even need to use the same learning approach for each training partition, you can use an ensemble of different techniques if you so desire). At the end of this stage, we have teacher models. The teacher models are then combined as an ensemble which makes predictions on inputs by querying each teacher for a prediction and aggregating the results into a single prediction.

When combining the ensemble’s votes to make the prediction, we don’t want to end up in a situation whereby a single teacher’s vote can make an observable difference (i.e., the top two predicted labels with vote counts differing by at most one). To introduce ambiguity, random noise is added to the vote counts. If the prediction of model on input is given by , then the prediction of the ensemble is given as:

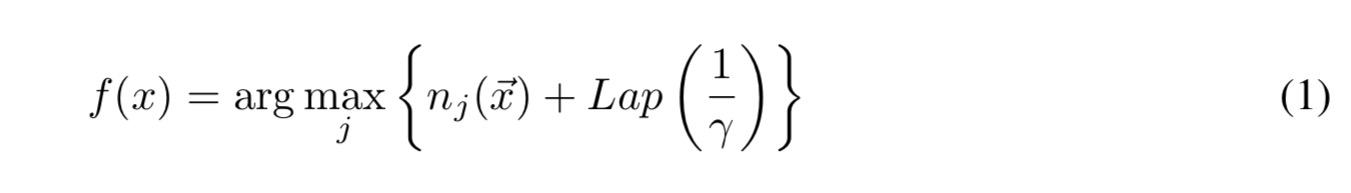
The privacy parameter influences the privacy guarantee that we can prove – the larger the value ofd the stronger the privacy guarantee, but the less accurate the predictions become. in the above equation refers to the Laplacian distribution with location 0 and scale .

The teacher ensemble is not deployed in any end-user facing application as its members were trained directly on sensitive data. Instead, a student model is trained to predict the output of the ensemble using auxiliary, unlabelled non-sensitive data. This approach does therefore require the availability of such unlabelled and non-sensitive data:

This assumption should not greatly restrict our method’s applicability: even when learning on sensitive data, a non-overlapping, unlabeled set of data often exists, from which semi-supervised methods can extract distribution priors. For instance, public datasets exist for text and images, and for medical data.

Here’s what the technique looks like end-to-end:

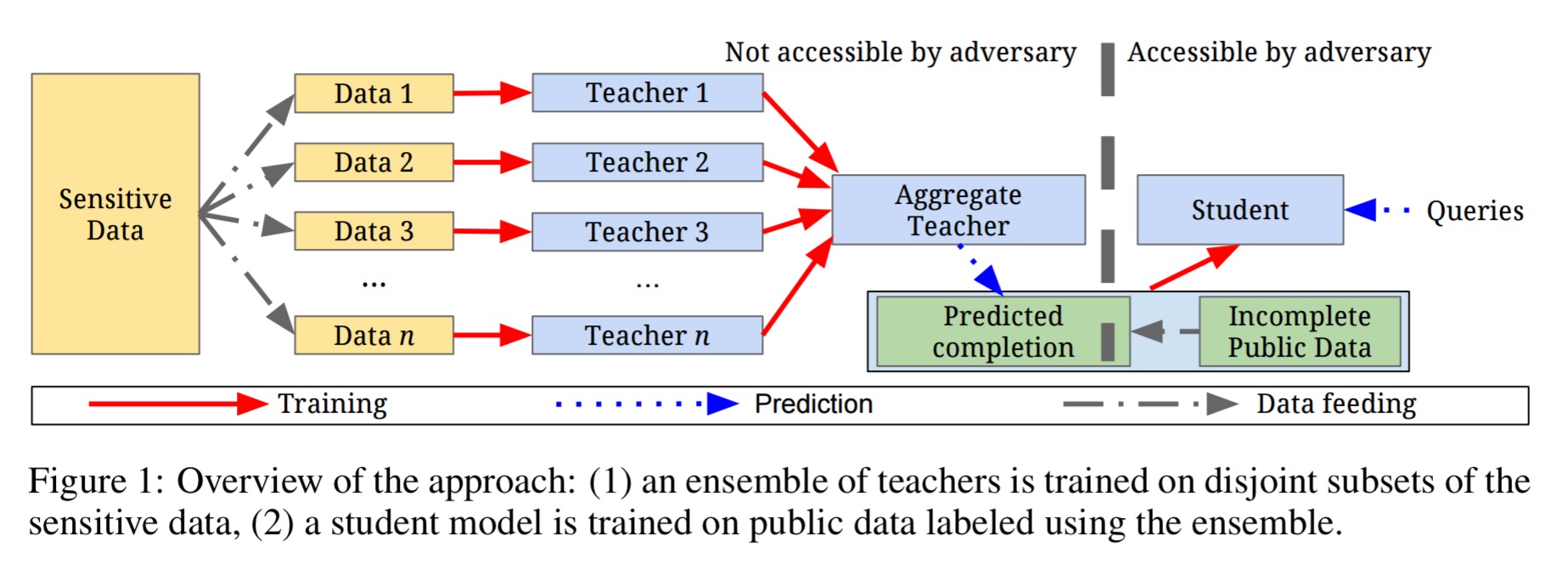
The student model is the one that is deployed in the final application. The student model has never directly seen any of the sensitive training examples. Furthermore, the amount of information revealed by the student model (privacy loss) is determined by the number of queries made to the teacher ensemble during student training. Most importantly, this means that the the deployed student model can be queried infinitely often with no further loss of privacy.

During training of the student model, we need to trade-off the student model’s quality with the number of labels it needs to access (number of queries it makes to the ensemble). Or put another way, how much of the nonsensitive data should be labelled by the ensemble for use in supervised learning.

Training the student in a semi-supervised fashion makes better use of the entire data available to the student, while still only labeling a subset of it. Unlabeled inputs are used in unsupervised learning to estimate a good prior for the distribution. Labeled inputs are then used for supervised learning.

After trying a few techniques, semi-supervised learning with GANs proved to be the most successful. Borrowing from Salimans et al. (2016) the following modifications were made to the standard generator and discriminator configuration:

• The discriminator is extended from a binary classifier (data vs generator sample) to a multi-class classifier (one of classes of data samples, plus a class for generated samples).
• The classifier is then trained to classify labeled real samples in the correct class, unlabeled real samples in any of the classes, and the generated samples in the additional class.

Privacy analysis

It seems intuitive, or even obvious, that a student machine learning model will provide good privacy when trained without access to sensitive training data, apart from a few, noisy votes from a teacher quorum. However, intuition is not sufficient because privacy properties can be surprisingly hard to reason about: for example, even a single data item can greatly impact machine learning models trained on a large corpus…

The authors apply the differential privacy framework to analyse the privacy offered by the PATE approach.

In other words, it puts an upper bound on what you can assume (or learn) about given you know something about . In the language of the original Dwork 2006 paper this is -approximate -indistinguishability. The analysis of the privacy offered by PATE builds on something call the moments accountant from Abadi et al. 2016. If label counts differ by at most 1 in each coordinate, then it is shown that we have -differential privacy. Over T steps (T queries made to the teacher ensemble), this becomes -differential privacy. Unfortunately, this results in fairly large values for : for the SVHN dataset it works out at , and on the MNIST dataset . But all is not lost…

Our data-dependent privacy analysis takes advantage of the fact that when the quorum among teachers is very strong, the majority outcome has overwhelming likelihood, in which case the privacy cost is small whenever this outcome occurs.

See section 3.3 in the paper for how the authors compute privacy bounds using the moments accountant under these circumstances. The script used to compute the bounds can be found in analysis.py at https://github.com/tensorflow/models/tree/master/differential_privacy/multiple_teachers.

Evaluation results

The framework is evaluated on MNIST and SVHN using ensembles of 250 teachers. The authors achieve -differential privacy with 98.00% accuracy, and -differential privacy with 90.66% accuracy respectively, improving the differential privacy state-of-the-art on these datasets. The non-private models used in the study achieved 99.18% and 92.8% accuracy respectively, indicating that the overall accuracy loss due to privacy is not too large.

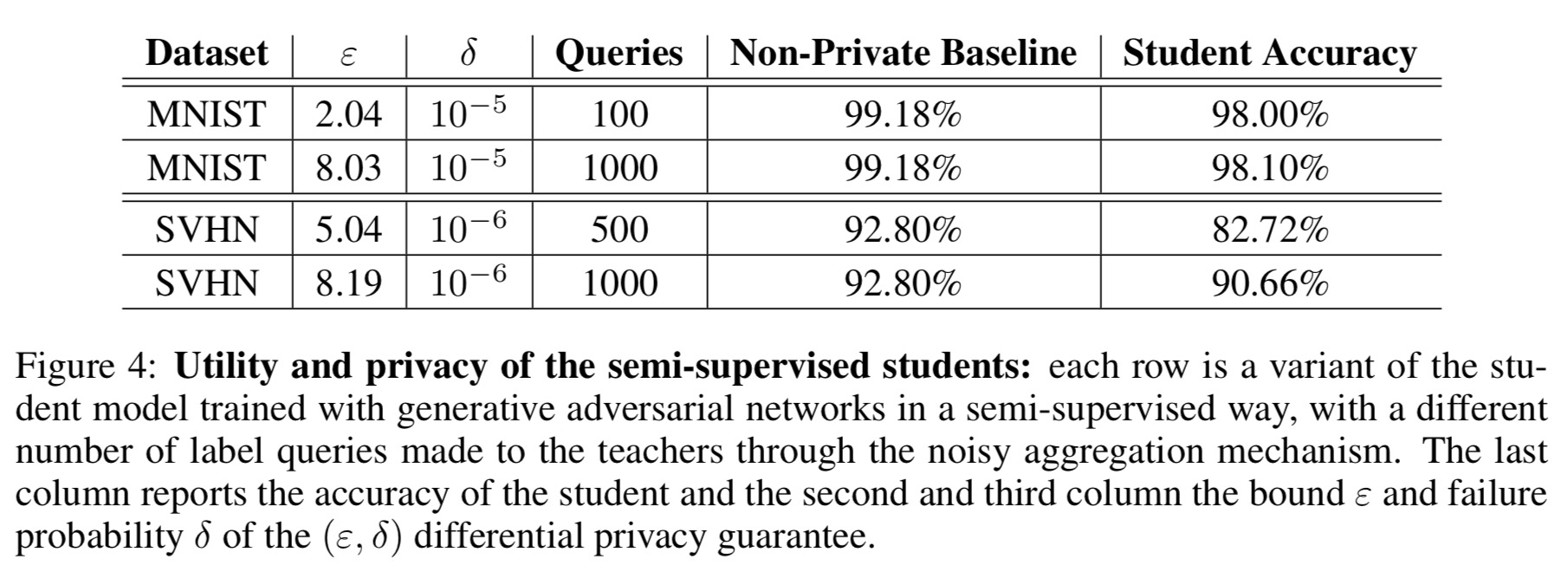
Our results are encouraging, and highlight the benefits of combining a learning strategy based on semi-supervised knowledge transfer with a precise, data-dependent privacy analysis. However, the most appealing aspect of this work is probably that its guarantees can be compelling to both an expert and non-expert audience. In combination, our techniques simultaneously provide both an intuitive and a rigorous guarantee of training data privacy, without sacrificing the utility of the targeted model.